3.6: The Cross Product- Algebra

Last updated
Save as PDF

Page ID: 125040

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

The Cross Product of two Vectors

A vector that is perpendicular to both vectors $\overrightarrow{u}\boldsymbol{=}\left\langle u_x,\left.u_y\right\rangle \right.$ and $\overrightarrow{v}\boldsymbol{=}\left\langle v_x,\left.v_y\right\rangle \right.$, can be found using the cross product. The cross product requires that both vectors be in three-dimensional space.

Definition: The Cross Product of two Vectors

The cross product of vectors $\vec{u}=\left\langle u_x, u_y, u_z\right\rangle$ and $\vec{v}=\left\langle v_x, v_y, v_z\right\rangle$ is a vector and is defined to be \[\vec{u} \times \vec{v}=\left\langle u_y v_z-u_z v_y, u_z v_x-u_x v_z, u_x v_y-u_y v_z\right\rangle \nonumber \]

This formula is challenging to remember. A nice device to help you remember both this formula and the dot product formula is to visualize them in a 3x3 square of components. The square shows how vectors can interact with one another.

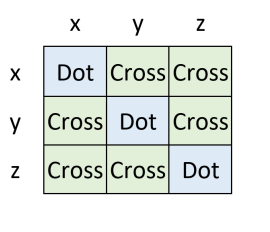
$Table showing a 3x3 square of components to help explain how vectors can interact with one another. The first column is labeled x, the second column is labeled y, and the third column is labeled z. The first row is labeled x, the second row is labeled y and the third row is labeled z. The box for row x, column x says Dot. The box for row x, column y says Cross, and the box for row x, column z says Cross. The box for row y, column x says Cross, the box for row y column y says Dot, and the box for row y column z says Cross. The box for row z column x says Cross, the box for row z, column y says Cross and the box for row z, column z says Dot.$

For the cross product,

The $x$-component has a product that involves no $x$-components: ${\ u}_yv_z-\ u_zv_y$

The $y$-component has a product that involves no $y$-components: ${\ u}_zv_x-u_xv_z$

The $z$-component has a product that involves no $z$-components: ${{\ u}_xv}_y\mathrm{-}\mathrm{\ }u_yv_z$

Each component is a difference of two diagonal products.

$Table showing a 3x3 square of components with examples of cross products. The first column is labeled x, the second column is labeled y, and the third column is labeled z. The first row is labeled x, the second row is labeled y and the third row is labeled z. The box for row x, column x says Dot. The box for row x, column y says x*y, and the box for row x, column z says x*z. The box for row y, column x says y*x, the box for row y column y says Dot, and the box for row y column z says y*z. The box for row z column x says z*x, the box for row z, column y says z*y, and the box for row z, column z says Dot.$

To produce the 𝑥𝑥-component, (top right) - (bottom left) = y*z – z*y

To produce the 𝑦𝑦-component, (bottom left) - (top right) = z*x – x*z

To produce the 𝑧𝑧-component, (top right) – (bottom left) = x*y – y*x

The DOT product is the interaction between two vectors having similar components:

\[x \cdot x, \quad y \cdot y, \quad z \cdot z \nonumber \]

The dot product measures similarity since it combines only interactions of matching components.

The CROSS product is the interaction between two vectors having different components:

\[x \cdot y, x \cdot z, y \cdot x, y \cdot z, z \cdot x, z \cdot y \nonumber \]

The cross product measures cross interactions since it combines interactions of different components.

Example $\PageIndex{1}$

Find the cross product of the vectors $\overrightarrow{u}\boldsymbol{=}\left\langle 5,\left.2,\ 4\right\rangle \right.$ and $\overrightarrow{v}\boldsymbol{=}\left\langle 3,\left.4,\ -7\right\rangle \right.$.

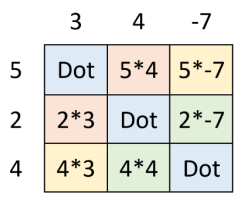
3x3 square table with columns labeled 3, 4, negative 7 and rows labeled 5, 2, 4. The box for row 5, column 3 says Dot, the box for row 5, column 4 says 5 multiplied by 4, and the box for row 5 column negative 7 says 5 multiplied by negative 7. The box for row 2, column 3 says 2 multiplied by 3, the box for row 2 column 4 says Dot and the box for row 2 column negative 7 says 2 multiplied by negative 7. The box for row 4 column 3 says 4 multiplied by 3, the box for row 4 column 4 says 4 multiplied by 4, and the box for row 4 column negative 7 says Dot.

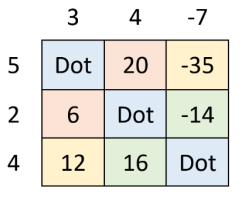
3x3 square table with columns labeled 3, 4, -7 and rows labeled 5, 2, 4. The box for row 5, column 3 says Dot, the box for row 5, column 4 says 20, and the box for row 5 column -7 says -35. The box for row 2, column 3 says 6, the box for row 2 column 4 says Dot and the box for row 2 column -7 says -14. The box for row 4 column 3 says 12, the box for row 4 column 4 says 16, and the box for row 4 column -7 says Dot.

Solution

To produce the $x$-component, (top right) - (bottom left) = 2*(-7) – 4*4 = -30

To produce the $y$-component, (bottom left) - (top right) = 4*3 – 5*(-7) = 47

To produce the $z$-component, (top right) – (bottom left) = 5*4 – 2*3 = 14

\[\overrightarrow{u}\times \overrightarrow{v}\boldsymbol{=}\left\langle -30,\ 47,\ \left.14\right\rangle \right. \nonumber \]

*Be careful with the computation. It goes (bottom left) – (top right) whilethe first and last go (top right) – (bottom left).

Using Technology

We can use technology to find the cross product between two vectors.

Go to www.wolframalpha.com

To find the cross product of the vectors $\overrightarrow{u}\boldsymbol{=}\left\langle 5,\left.2,\ 4\right\rangle \right.$ and $\overrightarrow{v}\boldsymbol{=}\left\langle 3,\left.4,\ -7\right\rangle \right.\boldsymbol{,\ }$use either the “cross” or the x command. Wolframalpha tells you what it thinks you entered, then it tells you its answer. In this case, $\overrightarrow{u}\times \overrightarrow{v}\boldsymbol{=}\left\langle -30,\ 47,\ \left.14\right\rangle \right.$.

This screenshot from WolframAlpha shows an evaluation of the cross product between vectors <5,2,4 and <3,4,negative 7>, or <5,2,4> x <3,4,negative 7>. The result is the vector (negative 30,47,14)." src="/@api/deki/files/97451/clipboard_e9640f1af100c5e766bbe45d473b19fb1.png">

The Right-Hand Rule

You can see that the cross product of the two vectors $\overrightarrow{u}$ and $\overrightarrow{v}$, is itself a vector. But where is this vector $\overrightarrow{u}\times \overrightarrow{v}?$ The cross product of two vectors is a vector that is perpendicular to the plane formed by the two vectors. What about the two perpendicular directions? Does this perpendicular vector lie above or below the plane formed by the two vectors? We use the right-hand rule.

Hold your hand as shown in the picture, your index and middle fingers extended. Your thumb points in the direction of the cross product.

$Illustration of a hand showing direction of fingers representing right-hand rule and the cross product of two vectors. The index finger is u, the middle finger v, and the thumb is the cross product u x v.$

Since the dot product is a scalar, it follows the properties of real numbers.

Properties of the Cross Product

$\vec{u} \times \vec{v}=-\vec{v} \times \vec{u}$, , the cross product is anti-commutative
$\vec{u} \times(\vec{v}+\vec{w})=\vec{u} \times \vec{v}+\vec{u} \times \vec{w}$, the cross product distributes over vector addition
$k(\vec{u} \times \vec{v})=(k \vec{u}) \times \vec{v}=\vec{u} \times(k \vec{u})$
$\vec{u} \times \overrightarrow{0}=\overrightarrow{0}$, the cross product with the zero vector $\vec{0}$, is the zero vector $\vec{0}$

Using Technology

For example, use WolframAlpha to compute both the cross product $\overrightarrow{u}\times \overrightarrow{v}$ and $\overrightarrow{v}\times \overrightarrow{u}$, with

$\overrightarrow{u}\boldsymbol{=}\left\langle 5,\left.-2,\ -3\right\rangle \right.$ and $\overrightarrow{v}\boldsymbol{=}\left\langle 6,\left.4,\ 1\right\rangle \right.$, to show that one is the opposite of the other.

This screenshot from WolframAlpha shows the cross product calculation <5,negative 2,negative 3 x <6,4,1>. The result is <10,negative 23,32>." src="/@api/deki/files/97453/clipboard_e067e85cbf91bc75737263e604bf16bbe.png">

This image from Wolfram Alpha shows the cross product calculation <6,4,1 x <5,negative 2,negative 3>. The result is . " src="/@api/deki/files/97454/clipboard_ecd2d30b29a40773d237cbeec0b738bb7.png">

Notice that $\left\langle 10,\left.-23,-32\right\rangle \right.=\ -\left\langle -10,\left.23,\ -32\right\rangle \right.$, verifying property 1.

Try These

Exercise $\PageIndex{1}$

Find the cross product of the vectors $\vec{u}=\langle 4,-2,1\rangle$ and $\vec{v}=\langle 5,-1,3\rangle$.

Answer: $\overrightarrow{u}\times \overrightarrow{v}\boldsymbol{=\ }\left\langle -5,\left.-7,\ 6\right\rangle \right.$

Exercise $\PageIndex{2}$

Find the cross product of the vectors $\vec{u}=\langle-2,3,-9\rangle$ and $\vec{v}=\langle-8,12,-36\rangle$.

Answer: $\overrightarrow{u}\times \overrightarrow{v}=\overrightarrow{0}$

Exercise $\PageIndex{3}$

Find $\vec{u} \times \vec{v} \cdot \vec{w}$, where $\vec{u}=\langle-2,5,3\rangle$, $\vec{v}=\langle 4,4,-2\rangle$, and $\vec{w}=\langle 2,6,-5\rangle$.

Answer: 144

* Note that the cross product must be computed first since if it is not, we would be crossing a vector with a scalar.

Search

Text Color

Text Size

Margin Size

Font Type

Definition: The Cross Product of two Vectors

Example \(\PageIndex{1}\)

Solution

Properties of the Cross Product

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)