4.6: Rotation Matrices in 3-Dimensions

Last updated
Save as PDF

Page ID: 125048

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

The Three Basic Rotations

A basic rotation of a vector in 3-dimensions is a rotation around one of the coordinate axes. We can rotate a vector counterclockwise through an angle $\theta$ around the $x$–axis, the $y$–axis, or the $z$–axis.

To get a counterclockwise view, imagine looking at an axis straight on toward the origin.

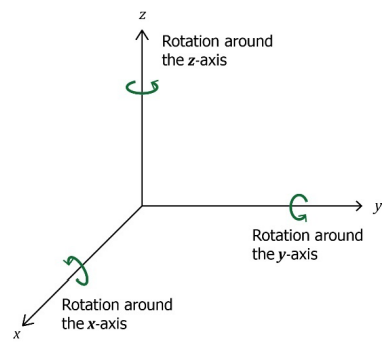
$This image shows rotations around each axis in the xyz-plane.$

Our plan is to rotate the vector $\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]$ counterclockwise around one of the axes through some angle $\theta$ to the new position given by the vector $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]$. To do so, we will use one of the three rotation matrices.

The Rotation Matrices

The rotation matrices for $x$, $y$, and $z$ axes are, respectively,

\[\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta
\end{array}\right] \quad\left[\begin{array}{ccc}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{array}\right] \quad\left[\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right] \nonumber \]

The Rotation Process

$x$–axis

To rotate the vector $\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]$ counterclockwise through an angle $\theta$ around the $x$–axis to a new position $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]$, perform the matrix multiplication,

\[\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta
\end{array}\right] \cdot\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] \nonumber \]

$y$–axis

To rotate the vector $\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]$ counterclockwise through an angle $\theta$ around the $y$–axis to a new position $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]$, perform the matrix multiplication,

\[\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{array}\right] \cdot\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] \nonumber \]

$z$–axis

To rotate the vector $\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]$ counterclockwise through an angle $\theta$ around the $z$–axis to a new position $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]$, perform the matrix multiplication,

\[\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right] \cdot\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right] \nonumber \]

Example $\PageIndex{1}$

Find the vector $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]$ that results when the vector $\left[ \begin{array}{c} x \\ y \\ z \end{array} \right]=\left[ \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right]$ is rotated 90° counterclockwise around $x$-axis.

Solution

Using the rotation formula $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta
\end{array}\right] \cdot\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]$ with $\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]$ and $\theta =90\mathrm{{}^\circ },$ we get

\[\begin{aligned}
& {\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\
0 & \sin \theta & \cos \theta
\end{array}\right] \cdot\left[\begin{array}{c}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & \cos 90^{\circ} & -\sin 90^{\circ} \\
0 & \sin 90^{\circ} & \cos 90^{\circ}
\end{array}\right] \cdot\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]} \\
& {\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & 0 & -1 \\
0 & 1 & 0
\end{array}\right] \cdot\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]=\left[\begin{array}{c}
1 \cdot 1+0 \cdot 2+0 \cdot 3 \\
0 \cdot 1+0 \cdot 2+(-1) \cdot 3 \\
0 \cdot 1+1 \cdot 2+0 \cdot 3
\end{array}\right]} \\
& {\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]=\left[\begin{array}{c}
1 \\
-3 \\
2
\end{array}\right]} \\
&
\end{aligned} \nonumber \]

When rotated counterclockwise 90° around the $x$–axis, the vector $\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]$ becomes $\left[\begin{array}{l}
1 \\
-3 \\
2
\end{array}\right]$.

Using Technology

We can use technology to help us find the rotation. WolframAlpha evaluates the trig functions for us.

Go to www.wolframalpha.com

Example $\PageIndex{2}$

In Example

Now we will use WolframAlpha to rotate vector $\left[ \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right]$ 90° around the $y$-axis. We use the$y$-axis rotation matrix $\left[\begin{array}{ccc}
\cos \theta & 0 & \sin \theta \\
0 & 1 & 0 \\
-\sin \theta & 0 & \cos \theta
\end{array}\right]$.

To perform the rotation, enter Evaluate $[[\cos (90), 0, \sin (90)],[0,1,0],[-\sin (90), 0, \cos (90)]] *[1,2,3]$ into the entry field.

Both entries and rows are separated by commas as WA does not see spaces.

Wolframalpha tells you what it thinks you entered, then tells you its answer.

$This screenshot from WolframAlpha shows what vector you get when you rotate vector [1,2,3] by 90 degrees. To do this, input Evaluate[[cos(90),0,sin(90)], [0,1,0], [–sin(90),0,cos(90)]] * [1,2,3]. The result is(3,2, negative 1).$

When rotated counterclockwise 90$\mathrm{{}^\circ}$ around the $y$–axis, the vector $\left[ \begin{array}{c} 1 \\ 2 \\ 3 \end{array} \right]$ becomes $\left[ \begin{array}{c} 3 \\ 2 \\ -1 \end{array} \right]$.

Example $\PageIndex{3}$

Solution

Since we are rotating the vector around the $z$–axis, we use the $z$-axis rotation matrix

\[\left[\begin{array}{ccc}
\cos \theta & -\sin \theta & 0 \\
\sin \theta & \cos \theta & 0 \\
0 & 0 & 1
\end{array}\right] \nonumber \]

Using WolframAlpha with $\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]$ and $\theta =45\mathrm{{}^\circ },$ we get

$This screenshot from WolframAlpha shows what vector you get when you rotate vector [1,2,3] by 45 degrees. To do this, input [[cos(45),-sin(45),0], [sin(45),cos(45),0],[0,0,1]] * [1,2,3]. The answer is [negative 1over the square root of 2,3 over the square root of 2,3].$

When rotated counterclockwise 45° around the $z$–axis, the vector $\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]$ becomes $\left[\begin{array}{c}
-1 / \sqrt{2} \\
3 / \sqrt{2} \\
3
\end{array}\right]$.

Try these

Find the vector $\left[\begin{array}{l}
x^{\prime} \\
y^{\prime} \\
z^{\prime}
\end{array}\right]$ that results when the given vector $\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]$ is rotated the given angle $\theta$ counterclockwise around the given axis.

Exercise $\PageIndex{1}$

$\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
1 \\
1
\end{array}\right]$ through 90° around the $x$-axis.

Answer: $\left[ \begin{array}{c} 1 \\ -1 \\ 1 \end{array} \right]$

Exercise $\PageIndex{2}$

$\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
0 \\
1
\end{array}\right]$ through 45° around the $z$-axis.

Answer: $\left[ \begin{array}{c} \sqrt{2} \\ 0 \\ 1 \end{array} \right]$

Exercise $\PageIndex{3}$

$\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3 \\
4 \\
5
\end{array}\right]$ through 30° around the $y$-axis

Answer: $\left[ \begin{array}{c} 3 \\ -5 \\ 4 \end{array} \right]$

Search

Example \(\PageIndex{1}\)

Solution

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Solution

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)

The Three Basic Rotations

The Rotation Matrices

The Rotation Process

\(x\)–axis

\(y\)–axis

\(z\)–axis

Example \(\PageIndex{1}\)

Solution

Using Technology

Example \(\PageIndex{2}\)

Example \(\PageIndex{3}\)

Solution

Try these

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Exercise \(\PageIndex{3}\)