1.8: Perimeter and Circumference

Last updated
Save as PDF

Page ID: 153112

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

You may use a calculator throughout this module if needed.

Perimeter

A polygon is a closed geometric figure with straight sides. Common polygons include triangles, squares, rectangles, parallelograms, trapezoids, pentagons, hexagons, octagons… Just as a perimeter fence runs along the outside edge of a region, the perimeter of a polygon is the total distance around the outside. In general, to find the perimeter of a polygon, you can add up the lengths of all of its sides.

Also, if you haven’t already, now is the time to get in the habit of including units in your answers.

Exercises

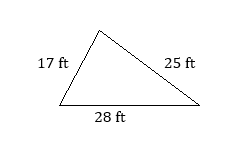
Find the perimeter of the triangle.
$triangle with sides labeled 17 ft, 25 ft, 28 ft$
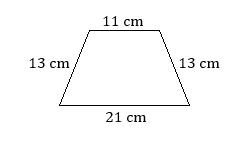
Find the perimeter of the trapezoid.
$trapezoid with sides labeled 13 cm, 11 cm, 13 cm, 21 cm$

If we know that some of the sides of a polygon are equal, we can use a formula as an alternative to adding up all of the lengths individually. The first formula shown below uses the variable $s$ for the side of a square. The rectangle formulas use $l$ for length and $w$ for width, or $b$ for base and $h$ for height; these terms are interchangeable.

Perimeter Formulas

Square: $P=4s$

Rectangle: $P=2l+2w$ or $P=2b+2h$

Rectangle: $P=2(l+w)$ or $P=2(b+h)$

Exercises

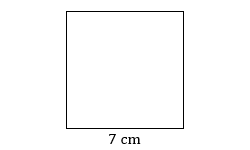
Find the perimeter of the square.
$square with bottom side labeled 7 cm$
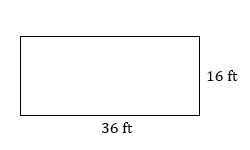
Find the perimeter of the rectangle.
$rectangle with right side labeled 16 ft and bottom side labeled 36 ft$
A storage area, which is a rectangle that is $45$ feet long and $20$ feet wide, needs to be fenced around all four sides. How many feet of fencing is required? (To keep it simple, ignore any gates or other complications.)
Giancarlo is putting crown molding around the edge of the ceiling of his living room. If the room is a $12$-foot by $16$-foot rectangle, how much crown molding does he need?

The sides of a regular polygon are all equal in length. Therefore, multiplying the length of a side by the number of sides will give us the perimeter.

Perimeter Formula

Regular Polygon with $n$ sides of length $s$: $P=n\cdot{s}$

Exercises

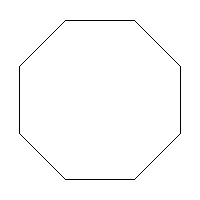
Find the perimeter of each regular polygon.

Each side of the hexagon is $4$ inches long.
$a regular hexagon with all 6 sides of equal length$
Each side of the octagon is $2.5$ centimeters long.
$a regular octagon with all 8 sides of equal length$

Circumference

The distance around the outside of a circle is called the circumference, rather than the perimeter. Let’s review some circle vocabulary before moving on.

Every point on a circle is the same distance from its center. This distance from the center to the edge of the circle is called the radius. The distance from one edge to another, through the center of the circle, is called the diameter. As you can see, the diameter is twice the length of the radius.

$a circle with a line from the center to the edge, labeled r$ $a circle with a line from edge to edge passing through the center, labeled d$

Throughout history, different civilizations have discovered that the circumference of a circle is slightly more than $3$ times the length of its diameter. (By the year 2000 BCE, the Babylonians were using the value $3\dfrac{1}{8}=3.125$ and the Egyptians were using the value $3\dfrac{13}{81}\approx3.1605$.)^[1] The value $3\dfrac{1}{7}\approx3.1429$ is an even better approximation for the ratio of the circumference to the diameter. However, the actual value cannot be written as an exact fraction; it is the irrational number $\pi$, pronounced “pie”, which is approximately $3.1416$.

Circumference Formulas

$C=\pi{d}$

$C=2\pi{r}$

Any scientific calculator will have a $\pi$ key; using this will give you the most accurate result, although you should be sure to round your answer appropriately. (Remember from Module 5 that we need to pay attention to significant figures when multiplying or dividing.) Many people use $3.14$ as an approximation for $\pi$, but this can lead to round-off error. If you must use an approximation for $\pi$, use $3.1416$.

Exercises

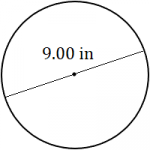
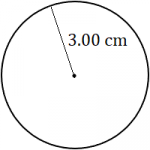
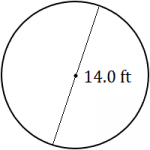
Calculate the circumference of each circle. Round each answer to the appropriate level of accuracy.

$circle with diameter measuring 9.00 inches$
$circle with radius measuring 3.00 centimeters$
$circle with diameter measuring 14.0 feet$
$circle with radius measuring 8.4 meters$

This information comes from Chapter 1 of the book A History of Pi by Petr Beckmann. It is a surprisingly interesting read. ↵

Search

Text Color

Text Size

Margin Size

Font Type

Exercises

Exercises

Exercises

Exercises