6.6: The Harmonic Series

The great foundation of mathematics is the principle of contradiction, or of identity, that is to say that a statement cannot be true and false at the same time, and that thus A is A, and cannot be not A. And this single principle is enough to prove the whole of arithmetic and the whole of geometry, that is to say all mathematical principles.

- Gottfried W. Leibniz (1646-1716)

We have seen how some infinite series, or sums that go on for ever, can be assigned a finite value for their sum:

$$1+r+r^2+r^3+\cdots (\text{for ever})=\frac{1}{1-r}$$ $$\frac{1}{1\cdot 2}+\frac{1}{2\cdot 3}+\frac{1}{3\cdot 4}+\cdots +\frac{1}{n(n+1)}+\cdots (\text{for ever})=1$$

\(\dfrac{1}{1^2}+\dfrac{1}{2^2}+\dfrac{1}{3^2}+\cdots+\dfrac{1}{n^2}+\cdots(\) for ever \()=\dfrac{\pi^2}{6} \notag \)

\(\dfrac{1}{0 !}+\dfrac{1}{1 !}+\dfrac{1}{2 !}+\cdots+\dfrac{1}{n !}+\cdots(\) for ever \()=e \notag \).

We say that these series converge (meaning that they can be assigned a finite value).

This section is concerned with another very natural series, the so-called harmonic series

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots (\text{for ever}).$$

It is not entirely clear why this is called the harmonic series. The natural overtones that arise in connection with plucking a stretched string (as with a guitar or a harp) have wavelengths that are $\genfrac{}{}{0.1ex}{}{1}{2}$ the basic wavelength, or $\genfrac{}{}{0.1ex}{}{1}{3}$ of the basic wavelength, and so on. It is also true that, just as each term of an arithmetic series is the arithmetic mean of its two neighbours, and each term of a geometric series is the geometric mean of its two neighbours, so each term of the harmonic series after the first is equal to the harmonic mean (see Problems 85., 89.) of its two neighbours:

$$\frac{1}{k}=\frac{2}{{\left(\frac{1}{k-1}\right)}^{-1}+{\left(\frac{1}{k+1}\right)}^{-1}}.$$

Unlike the first two series above, there is no obvious closed formula for the finite sum

$$s_n=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}.$$

Certainly the sequence of successive sums

$$s_1=1,s_2=\frac{3}{2},s_3=\frac{11}{6},s_4=\frac{25}{12},s_5=\frac{137}{60},\dots$$

does not suggest any general pattern.

Problem 252 Suppose we denote by S the “value” of the endless sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(for ever)}$$

(i) Write out the endless sum corresponding to “$$12S”.

(ii) Remove the terms of this endless sum from the endless sum S, to obtain another endless sum corresponding to “$S-$12S” $=$12S.

(iii) Compare the first term of the series in (i) (namely $\genfrac{}{}{0.1ex}{}{1}{2}$) with the first term in the series in (ii) (namely 1); compare the second term in the series in (i) with the second term in the series in (ii); and so on. What do you notice?

The Leibniz quotation above emphasizes that the reliability of mathematics stems from a single principle – namely the refusal to tolerate a contradiction. We have already made explicit use of this principle from time to time (see, for example, the solution to Problem 125.). The message is simple: whenever we hit a contradiction, we know that we have “gone wrong” – either by making an error in calculation or logic, or by beginning with a false assumption. In Problem 252. the observations you were expected to make are paradoxical: you obtained two different series, which both correspond to “$$12S”, but every term in one series is larger than the corresponding term in the other! What one can conclude may not be entirely clear. But it is certainly clear that something is wrong: we have somehow created a contradiction. The three steps ((i), (ii), (iii)) appear to be relatively sensible. But the final observation “$$12S<12S” (since $\frac{1}{2}<1$, $\frac{1}{4}<\frac{1}{3}$, etc.) makes no sense. And the only obvious assumption we have made is to assume that the endless sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(for ever)}$$

can be assigned a value “S”, which can then be manipulated as though it were a number.

The conclusion would seem to be that, whether or not the endless sum has a meaning, it cannot be assigned a value in this way. We say that the series diverges. Each finite sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}$$

has a value, and these values “grow more and more slowly” as n increases:

• the first term immediately makes the sum = 1
• it takes 4 terms to obtain a sum > 2;
• it takes 11 terms to obtain a sum > 3; and
• it takes $12367$ terms before the series reaches a sum > 10.

However, this slow growth is not enough to guarantee that the corresponding endless sum corresponds to a finite numerical value.

The danger signals should already have been apparent in Problem 249., where you proved that

$$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}\ge \sqrt{n}$$

The $n^{\mathrm{th}}$ term $\frac{1}{\sqrt{n}}$ tends to 0 as n increases; so the finite sums grow ever more slowly as n increases. However, the LHS can be made larger than any integer K simply by taking K² terms. Hence there is no way to assign a finite value to the endless sum

$$\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+\cdots +\frac{1}{\sqrt{n}}+\cdots (\text{for ever}).$$

Problem 253.

(a)(i) Explain why

$$\frac{1}{2}+\frac{1}{3}<1.$$(ii) Explain why

\(\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}<1 \notag \)

(iii) Extend parts (i) and (ii) to prove that

\(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{2^n-1}<n\), for all \(n \geq 2 \notag \)

(iv) Finally use the fact that, when $n\ge 3$,

\(\dfrac{1}{2^n}<\dfrac{1}{2}-\dfrac{1}{3} \notag \)

to modify the proof in (iii) slightly, and hence show that

\(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{2^n}<n\), for all \(n \geq 3\).

$$\frac{\mathrm{}}{}$$

(b)(i) Explain why

$$\frac{1}{3}+\frac{1}{4}>\frac{1}{2}.$$

(ii) Explain why

$$\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}>\frac{1}{2}.$$

(iii) Extend parts (i) and (ii) to prove that$$$$

\(\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{2^n}>1+\dfrac{n}{2}\), for all \(n \geq 2 \notag \)

(c) Combine parts (a) and (b) to show that, for all $n\ge 2$, we have the two inequalities$$$$

\(1+\dfrac{n}{2}<\dfrac{1}{1}+\dfrac{1}{2}+\dfrac{1}{3}+\cdots+\dfrac{1}{2^n}<n \notag \).

$$$$Conclude that the endless sum

$$\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}+\cdots \text{(for ever)}$$

cannot be assigned a finite value.

The result in Problem 253.(c) has an unexpected consequence.

Problem 254 Imagine that you have an unlimited supply of identical rectangular strips of length 2. (Identical empty plastic CD cases can serve as a useful illustration, provided one focuses on their rectangular side profile, rather than the almost square frontal cross-section.) The goal is to construct a ‘stack’ in such a way as to stick out as far as possible beyond a table edge. One strip balances exactly at its midpoint, so can protrude a total distance of 1 without tipping over.

(a) Arrange a stack of n strips of length 2, one on top of the other, with the bottom strip protruding distance $\frac{1}{n}$ beyond the edge of the table, the second strip from the bottom protruding $\frac{1}{n-1}$ beyond the leading edge of the bottom strip, the third strip from the bottom protruding $\frac{1}{n-2}$ beyond the leading edge of the strip below it, and so on until the ${(n-1)}^{\text{th}}$ strip from the bottom protrudes distance $\genfrac{}{}{0.1ex}{}{1}{2}$ beyond the leading edge of the strip below it, and the top strip protrudes distance 1 beyond the leading edge of the strip below it (see Figure 10). Prove that a stack of n identical strips arranged in this way will just avoid tipping over the table edge.

(b) Conclude that we can choose n so that an arrangement of n strips can (in theory) protrude as far beyond the edge of the table as we wish – without tipping.

The next problem illustrates, in the context of the harmonic series, what is in fact a completely general phenomenon: an endless sum of steadily decreasing positive terms may converge or diverge; but provided the terms themselves converge to 0, then the the corresponding “alternating sum” – where the same terms are combined but with alternately positive and negative signs – always converges.

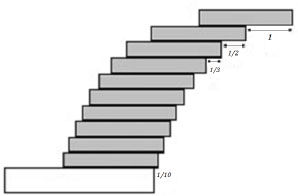
Figure 10: Overhanging strips, n = 10.

Problem 255

(a) Let

$$s_n=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \pm \frac{1}{n}$$

(where the final operation is “+” if n is odd and “-” if n is even).

(i) Prove that

\(s_{2 n-2}<s_{2 n}<s_{2 m+1}<s_{2 m-1} \notag \)

$${}_{}$$

(ii) Conclude that the endless alternating sum

\(\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots \notag \) (for ever)

can be assigned a value s that lies somewhere between $s_6=\frac{37}{60}$ and $s_5=\frac{47}{60}$.

(b) Let

$$a_1,a_2,a_3,\dots$$

be an endless, decreasing sequence of positive terms (that is, $a_{n+1}<a_n$ for all $n\ge 1$). Suppose that the sequence of terms $a_n$ converges to 0 as $n\to \infty$.

(i) Let

$$s_n=a_1-a_2+a_3-a_4+a_5-\cdots \pm a_n$$

(where the final operation is “+” if n is odd and “−” if n is even). Prove that

\(s_{2 n-2}<s_{2 n}<s_{2 m+1}<s_{2 m-1}\), for all \(m, n \geq 1 \notag \)

$${}_s$$$${}_{}$$
(ii) Conclude that the endless alternating sum

$$a_1-a_2+a_3-a_4+a_5-\cdots \text{(for ever)}$$

can be assigned a value s that lies somewhere between $s_2=a_1-a_2$ and $s_3=a_1-a_2+a_3$.

Just as with the series

\(\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots+\frac{1}{n^2}+\cdots \notag\) (for ever)

$$\frac{\mathrm{}}{}$$
$$\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\cdots +\frac{1}{n!}+\cdots (\text{for ever}),$$

we can show relatively easily that

$$\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\frac{1}{5}-\cdots (\text{for ever})$$

can be assigned a value s. It is far less clear whether this value has a familiar name! (It is in fact equal to the natural logarithm of 2: “$$\(\log _e 2\)”.) A similarly intriguing series is the alternating series of odd terms from the harmonic series:$$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\cdots (\text{for ever})$$

You should be able to show that this endless series can be assigned a value somewhere between $s_2=\frac{2}{3}$ and $s_3=\frac{13}{15}$; but you are most unlikely to guess that its value is equal to $\frac{}{}$\(\frac{\pi}{4}\). This was first discovered in 1674 by Leibniz (1646-1716). One way to obtain the result is using the integral of ${(1+x^2)}^{-1}$ from 0 to 1: on the one hand the integral is equal to $$arctan x evaluated when $x=1$ (that is, $\frac{}{}$\(\frac{\pi}{4}\)); on the other hand, we can expand the integrand as a power series $1-x^2+x^4-x^6+\cdots$, integrate term by term, and prove that the resulting series converges when $x=1$. (It does indeed converge, though it does so very, very slowly.)

The fact that the alternating harmonic series has the value \(\log _e 2\) seems to have been first shown by Euler (1707-1783), using the power series expansion for $\log (1+x)$.