Solutions
- Page ID
- 70988
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Module 1 Set Theory
Exercise Set 1 Solutions
| a. 5P, 6P, 7P, 8P | ||||||
| b. 4D, 5D, 6D, 7D, 8D, 9D | ||||||
| c. 5H, 6H, 7H, 9H | ||||||
|
d. There are 6 groups. You should have listed 2 of these groups:
|
5. a collection of objects
6. the objects in a set
7. The null set is a set that contains no elements that is, it is empty.
9. Yes.
| N = {4N, 5N, 6N, 7N, 8N} |
| Q = {4Q, 5Q, 6Q, 7Q, 8Q, 9Q} |
| S = {4N, 4D, 4Q} |
| W = {6P, 6N, 6D, 6Q, 6H} |
| Y = {8P, 8N, 8D, 8Q} |
| T = { } |
10.
|
a. yes; any element of N will suffice 4N, 5N, 6N, 7N or 8N |
b. no | c. no | d. yes |
11. Answers may vary. Any element in P will suffice 5P, 6P, 7P or 8P
12.
| a. F | b. T | c. T | d. T | e. F |
| f. T | g. T | h. T | i. F |
| a. 4 | b. 5 | c. 6 | d. 6 | e. 3 | f. 4 |
| g. 4 | h. 0 | i. 3 | j. 5 | k. 5 | l. 5 |
| m. 25 | n. 0 | o. Z ~ S; P~H, H ~ Y; N ~ W;X ~ V; Q ~ D (it's not necessary to include any null subsets) |
15.
| a. Ø | b. {9H} | c. {4H} |
| d. {6Q} | e. Ø |
17. Two sets, A and B, are disjoint if \(A \cap B = Ø\) that is to say that their intersection is empty.
18. 5D, 6P, 7P, 8P, 5P, 5N, 5Q, 5H. yes, there are 8 coins.
19.
| a. {4N, 5N, 6N, 7N, 8N, 4D, 4Q} |
| b. {4Q, 5Q, 6Q, 7Q, 8Q, 9Q, 6P, 6N, 6D, 6H} |
| c. {5P, 6P, 7P, 8P, 4D, 5D, 6D, 7D, 8D, 9D} |
| d. {7P, 7N, 7D, 7Q, 7H, 8P, 8N, 8D, 8Q} |
23.
| a. {2, 4} | b. {3, 5} |
| c. { } or Ø | d. {1, 2, 3, 4, 5, 6, 8} |
| e. {1, 2, 3, 4, 5, 7} | f. {2, 3, 4, 5, 6, 7, 8} |
| g. {6, 7, 8, 9} | h. {1, 3, 5, 7, 9} |
| i. {1, 2, 4, 6, 8, 9} | p. {1, 3, 5, 7} |
| j. {1, 3, 5} | q. {3, 5, 6, 7, 8, 9} |
| k. {6, 8} | r. {2,3,4,5,7} |
| l. {1, 2, 4} | s. {2, 4} |
| m. {7} | t. {6, 8, 9} |
| n. B or {2,4,6,8} | u. {7, 9} |
| o. C or {3,5,7} | v. {1, 3, 5, 6, 7, 8, 9} |
| w. {7, 9} | x. {3, 5, 6, 7, 8, 9} |
| y. T | z. T |
| aa. F | bb. F |
| cc. T | dd. F |
| ee. T | ff. F |
| gg. F | hh. T |
| ii. T | jj. F |
25.
| a. {a, b, c, ..., z} |
| b. {124, 126, 128, ..., 698} |
| c. {101, 102, 103, ..., 999} |
| d. {x|x is a past president of the U.S. up until 1995} |
| e. {Reagan, Bush, Clinton} |
30.
| a. 3; 8; answers may vary |
| b. 4; 6; answers may vary |
| c. 2; 12; answers may vary |
| d. 12; 2; answers may vary |
| e. 8; 3; answers may vary |
| f. 6; 4; answers may vary |
31. e. union
32.
| c. no |
| d. yes; LYC, LYQ, LYT |
| e. intersection;{LYC, LYQ, LYT} |
34.
| a. {} |
| b. {}, {P} |
| c. { }, {G},{F}, {F,G} |
| d. {}, {X}, {Y}, {Z}, {X,Y}, {X,Z}, {Y,Z}, {X,Y,Z} |
| e. { }, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 4}, {3, 4}, {1, 2, 3}, {1, 2, 4}, {1, 3, 4}, {2, 3, 4}, {1, 2, 3, 4} |
35.
| a. 1 | b. 2 | c. 4 | d. 8 |
| e. 16 | f. 32 | g. \(2^{n}\) |
36. 35
37. 35
38. yes
39.
| a. bc | b. \(b^{2}\) | c. \(c^{2}\) |
40. One possibility is let A = {m} and B = {n}. Then \(A \times B = {(m,n)}\) but \(B \times A = {(n,m)}\). Therefore, \(A \times B \nleq B \times A\) (be sure to write your own solution)
41.
| a. {(3,2), (3,6), (4,2), (4,6)} |
| b. {(6,5), (7,5), (8,5), (9,5)} |
| c. { } |
| d. {(a,a)} |
| e. {(x,x), (x,y), (y,x), (y,y)} |
| f. {(1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5)} |
| g. {((9,4),D), ((9,4), {a,b,c}), (C,D), (C, {a,b,c})} |
| h. {({5,6,7,8,9}, g), ({5,6,7,8,9},{4,3})} |
Exercise Set 2 Solutions

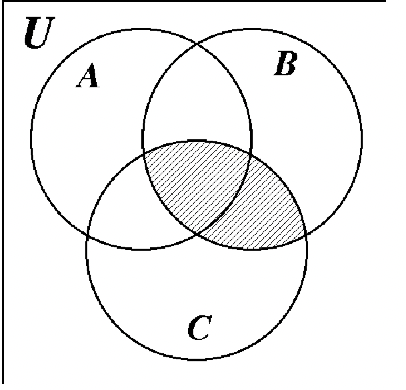
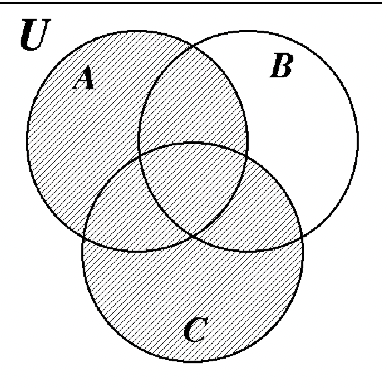



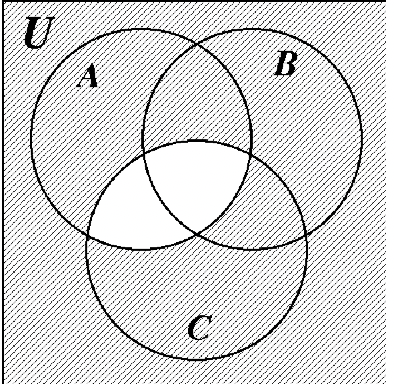


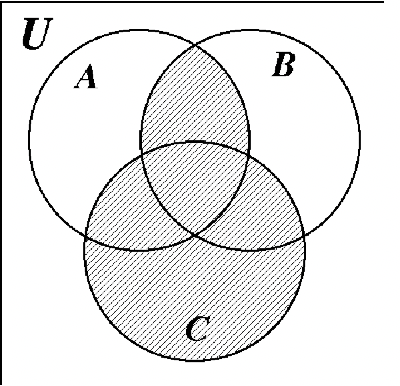






18-56: Answers to these exercises are the Venn diagrams at the end of Exercise Set 2.
Exercise Set 3 Solutions
1. Answers may vary. The overlap is the intersection. There are 8 regions.
2.
|
a.  |
b.  |
|
c.  |
d.  |
4.
|
a.  |
|
b.  |
|
c.  |
5. Some possibilities are: triangle, circle, square; large, small and any other value.
8.
|
a.  |
| b. SRT, SYT, SGT, LGT, SYC, LYT, SRC, SGC, LRT, LGC, LRC, LYC |
| c. SRT, SYT, SGT, LGT, SYC, LYT, SRC, SGC, LRT, LGC, LRC, LYC |
| d. The elements are exactly the same |
| e. \(B \cup Q)^{c} = B^{c} \cap Q^{c}\) |
9.
|
a.  |
| b. SRT, LRQ, LRT, SRQ |
| c. SRT, LRQ, LRT, SRQ |
| d. The elements are exactly the same. |
| e. \((R^{c} \cup C)^{c} = R \cap C^{c}\) |
10. For part a and b, the final shadings are the same as shown on the Venn diagram below. The equation you can write is: \((B \cup Q)^{c} = B^{c} \cap Q^{c}\)

11. For part a and b, the final shadings are the same as shown on the Venn diagram below. The equation you can write is: \((A \cap B)^{c} = A^{c} \cup B^{c}\)

12.
| a. \(R \cup S\) | b. (\(M^{c} \cup N^{c})^{c}\) | c. \(F^{c} \cap G\) | d. \((H \cap I^{c})^{c}\) | e. \(P \cup Q^{c}\) | f. \((S^{c} \cup T)^{c}\) |
14. Only a proof to 14.c. is provided
|
\((B^{c} \cup C)^{c} = (({2, 4, 6, 8}}}^{c} \cup {3, 5, 7}^{c}\) = \({1, 3, 5, 7, 9} \cup {3, 5, 6})^{c}\) = \(({1, 3, 5, 7, 9})^{c}\) = {2, 4, 6, 8}. |
|
\(B \cap C^{c} = {2, 4, 6, 8} \cap ({1, 3, 5, 7, 9})^{c}\) = \({2, 4, 6, 8} \cap {2, 4, 6, 8}\) = {2, 4, 6, 8}. |
Since \((B^{c} \cup C)^{c}\) and \(B \cap C^{C}\) have the exact same elements, they are equal. Therefore, \((B^{c} \cup C)^{c} = B \cap C^{c}\).
15.
|
a, b: final shadings are the same as shown on the Venn diagram below.  |
| c. {2,3,4,5} |
| d. {2,3,4,5} |
| e. They are the same equal. |
16.
|
a, b: final shadings are the same as shown on the Venn diagram below.  |
| c. {1,2,3,4,5} |
| d. {1,2,3,4,5} |
| e. They are the same. |
17.
| a. (\(X \cap Y) \cup (X \cap Z\)) |
| b. \((P \cup Q^{c}) \cap (P \cup R\)) |
| c. \(K^{c} \cap (L \cup M)\) |
| d. \(D \cup (E^{c} \cap F\)) |
Exercise Set 4 Solutions
1.

2.

3.
| a. \((A \cup B \cup C)^{c}\) | b. A - (\(B \cup C)\) |
| c. (A \cap B) - C | d. B - (\(A \cup C)\) |
| e. \((A \cap B \cap C\)) | f. \((A \cap C) - B\) |
| g. \((B \cap C) - A\) | h. \(C - \(A \cup B)\) |
4.
| a. 43 | b. 51 | c. 46 | d. 38 |
| e. 18 | f. 25 | g. 13 | h. 89 |
5.
| a. n(\(A - (B \cup C)\)) = 11 |
| b. n(A) = 69 |
| c. n(\(B \cap C\)) = 51 |
| d. n(\((A \cup B) - C\)) = 71 |
| e. n(\(C^{c}\)) = 73 |
| f. n(\(B \cup C\)) = 160 |
| g. n(B - C) = 60 |
| h. n(\((A \cap B) \cup (B \cap C) \cup (A \cap C)\)) = 66 |
| i. n(\((A \cap B) \cup (B \cap C) \cup (A \cap C) - (A \cap B \cap C)\)) = 23 |
6.
| a. 34 | b. 5 | c. 69 | d. 37 | e. 13 |
| f. 3 | g. 21 | h. 9 | i. 23 |
7.
|
a. 12  |
b. 2 | c. 6 |
8.
| a. 9 | b. 5 | c. 10 | d. 43 |
|
e. 37  |
f. 18 | g. 3 |
9.
| a. 86 | b. 49 | c. 31 |
| d. 25 | e. 4 | f. 27 |

10. This is one way to show it.
11. This is one way to show it.

12. This is one way to show it.
Homework Solutions
1.
| a. {a, c} |
| c. {e, v, w, z} |
| e. {r, u, x} |
| g. {a, c, r, u} |
| i. {x} |
| k. Ø or { } |
| m. 10 |
| n. 2 |
3. a. \((N^{c} \cap P)^{c}\)
4. a. \(A^{c} \cup (E \cap F\))
5.
|
a.  |
| c. 15 |
| e. 5 |
| g. 9 |
6.
| a. 8 | b. 3 |
7.
| a. T | c. F | e. T |
8.
|
a.  |
c.  |
e.  |
9. a. \(A \cup (B \cap C)\)
10.
a. { }
c. { }, {a}, {b}, {a, b}
11.
| a. {(1, 1), (1, 2), (1, 4), (2, 1), (2, 2), (2, 4), (4, 1), (4, 2), (4, 4)} |
| c. {({a, c}, {a, c}), ({a, c}, 5), (5, {a, c}), (5, 5)} |
| e. {(x, x)} |
12.
| a. {LBC, LYC, LGC} |
| c. {LRC, LBC, LGC, LYC, SRC} |
Module 2 Counting and Numerals
Exercise Set 1 Solutions
8. The sets have the same number of elements. Cardinality is equal.
10.
|
a) 1) \(1 \leftrightarrow A\) |
|
b. 1) \(2 \leftrightarrow B, 3 \leftrightarrow C\) 2) \(2 \leftrightarrow C, 3 \leftrightarrow B\) |
|
c. 1) \(4 leftrightarrow D, 5 leftrightarrow E, 6 leftrightarrow F\) 2) \(4 leftrightarrow D, 5 leftrightarrow F, 6 leftrightarrow E\) 3) \(4 leftrightarrow E, 5 leftrightarrow D, 6 leftrightarrow F\) 4) \(4 leftrightarrow E, 5 leftrightarrow F, 6 leftrightarrow D\) 5) \(4 leftrightarrow F, 5 leftrightarrow D, 6 leftrightarrow E\) 6) \(4 leftrightarrow F, 5 leftrightarrow E, 6 leftrightarrow D\) |
11.
|
a) 1) \(M \leftrightarrow M\) |
|
b. 1) \(x \leftrightarrow x, y \leftrightarrow z\) 2) \(x \leftrightarrow z, y \leftrightarrow x\) |
|
c. 1) \(1 \leftrightarrow 1, 2 \leftrightarrow 2\) 2) \(1 \leftrightarrow 2, 2 \leftrightarrow 1\) |
|
d. 1) \(1 \leftrightarrow 1, 2 \leftrightarrow 2, 3 \leftrightarrow 3\) 2) \(1 \leftrightarrow 1, 2 \leftrightarrow 3, 3 \leftrightarrow 2\) 3) \(1 \leftrightarrow 2, 2 \leftrightarrow 1, 3 \leftrightarrow 3\) 4) \(1 \leftrightarrow 2, 2 \leftrightarrow 3, 3 \leftrightarrow 1\) 5) \(1 \leftrightarrow 3, 2 \leftrightarrow 1, 3 \leftrightarrow 2\) 6) \(1 \leftrightarrow 3, 2 \leftrightarrow 2, 3 \leftrightarrow 1\) |
|
e. 1) \(1 \leftrightarrow 3, 2 \leftrightarrow 4, 3 \leftrightarrow 5\) 2) \(1 \leftrightarrow 3, 2 \leftrightarrow 5, 3 \leftrightarrow 4\) 3) \(1 \leftrightarrow 4, 2 \leftrightarrow 3, 3 \leftrightarrow 5\) 4) 1 \leftrightarrow 4, 2 \leftrightarrow 5, 3 \leftrightarrow 3 5) 1 \leftrightarrow 5, 2 \leftrightarrow 3, 3 \leftrightarrow 4 6) 1 \leftrightarrow 5, 2 \leftrightarrow 4, 3 \leftrightarrow 3 |
12.
| a. 1 | b. 2 | c. 6 |
14.
| a. | | | | | | | | | | | |
| b. Make 512 stroke marks; make 2,000,000 stroke marks. |
16.
| a. | | | | | | | | | | | | | | | | | |
|
b.  |
17. 36
18. Answers may vary. Some possibilities are to make 123 strokes or to make 8 I's and 53 strokes.
19.
| a. 301,020 | b. 4,010,507 |
| c. 35,000 | d. 110,023 |
20.
|
a.  |
|
b.  |
|
c.  |
|
d. 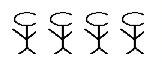 |
|
e.  |
21. Base Ten. They only have symbols up to a million in Egyptian. This makes writing very large numerals too cumbersome and possibly virtually impossible.
24.
| a. XXXII | b. DLXI |
| c. DCCVIII | d. MMLIII |
25.
| a. 2,687 | b. 1,232 |
26.
| a. \(\bar{\text{CCCXXX}}\)DCCCII |
| b. \(\bar{\bar{\text{LXX}}}\)MDCLI |
27.
| a. CCCCCCCCCXXXXIIII or DCCCCXXXXIIII |
| b. CCCCXXXXXXXXXIIIIIIIII or CCCCLXXXXVIIII |
29.
| a. DCCXLVIII |
| b. \(\bar{\text{XIV}}\)CDLXXX |
| c. CMLXIX |
| d. CDXLII |
30.
| a. \(\bar{\text{XIX}}\)CDLIII |
| b. MMDCCCXLIX |
| c. MCMXCVI |
32. 3, 1, 3, 1, 3, 1
33.
| a. 10 | b. 1 | c. 2 |
| d. 7 | e. 7 |
34.
| a. 3 |
| b. 2 |
| c. 9 |
| d. 900 strokes |
| e. 180 5 stroke tallies |
35.
Hindu-Arabic: 3, 3, 7, 5, 4
Stroke: 143, 400, 1000000, 30009, 2124
Tally: 31, 80, 200000, 6005, 428
Egyptian: 8, 4, 1, 12, 9
Roman: 6, 2, 1, 5, 7
Exercise Set 2 Solutions
1.
|
a. 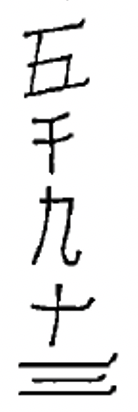 |
b.  |
c.  |
d.  |
2.
| a. 109 | b. 6063 | c. 40 | d. 2815 | e.7800 |
3.
|
1.  |
5.  |
9.  |
13.  |
17.  |
|
2.  |
6.  |
10.  |
14.  |
18.  |
|
3.  |
7.  |
11.  |
15.  |
|
|
4.  |
8.  |
12.  |
16.  |
19.  |
4. A dot represents the number one and a line segment represents the number five. Any combination of 1-3 line segments and/or 1-4 dots forms any numeral up to 19.
5.
| a. 90 | b. 320 | c. 162 |
6.
| a. 3974 | b. 1946 | c. 3300 |
| d. 32454 | e. 7319 |
7.
|
a.  |
b.  |
c. 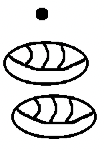 |
d. 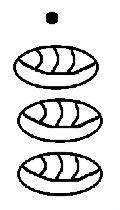 |
e.  |
8.
| a. 27 rem. 156 |
| b. 9 rem. 6709 |
| c. 16 rem. 13 |
| d. 2 rem. 142040 |
9. A 19 at the second level up is 380. The Mayan numeral for 380 is shown below.
10. You can't have higher than the 17 at the second level up because 18 at that level represents 360, which should be represented on the third level up. For all other levels, the highest numeral can be 19.
11.
|
a.  |
b.  |
c. 
 |
d.  |
e. |
12.
|
a.  |
b.  |
c.  |
13.
| a. 10 | b. 12 | c. 3 |
14.
| Chinese | Mayan | |
| a. 15 |
 |
 |
| b. 100 |
 |
 |
| c. 1000 |
 |
 |
| d. 9999 |
 |
 |
Exercise Set 3 Solutions
1.
| a. 2 | b. 2 | c. 2 | d. 2 | e. 2 |
2.
| a. 27 | b. 13, 1, 14 |
| c. 6, 1, 1, 8 | d. 3, 0, 1, 1, 5 |
| e. 1, 1, 0, 1, 1, 4 | f. 1, 1, 0, 1, 1 |
| g. 27, 4 |
3.
| a. 18 | b. 9, 0, 9 |
| c. 4, 1, 0, 5 | d. 2, 0, 1, 0, 3 |
| e. 1, 0, 0, 1, 0, 2 | f. 1, 0, 0, 1, 0 |
4.
| a. 45 | b. 22, 1, 23 |
| c. 11, 0, 1, 12 | d. 5, 1, 0, 1, 7 |
| e. 2, 1, 1, 0, 1, 5 | |
| f. 1, 0, 1, 1, 0, 1, 4 | |
| g. 1, 0, 1, 1, 0, 1 |
5.
| a. three, zero, two, base six |
| b. one, zero, one, one, base two |
| c. four, three, five, base seven |
6.
| a. \(5016_{\text{eight}}\) | b. \(101001_{\text{two}}\) |
7.
| 2048, 1024, 512, 256, ... |
8.
| a. 19 | b. 65 | c. 63 |
9. 3125, 625, 125, 25, 5, 1
10. 8
11. 2187, 729, 243, 81, 27, 9, 3, 1
12.
| a. 500 | b. 3711 | c. 1093 |
13.
| a. Six: 7776, 1296, 216, 36, 6, 1 |
| b. Seven: 16807, 2401, 343, 49, 7, 1 |
| c. Nine: 59049, 6561, 729, 81, 9, 1 |
| d. Eight: 32768, 4096, 512, 64, 8, 1 |
| e. Four: 1024, 256, 64, 16, 4, 1 |
| f. Ten: 100000,10000,1000,100,10,1 |
| g. Twelve: 20736, 1728, 144, 12, 1 |
| h. Eleven: 14641, 1331, 121, 11, 1 |
14. \(n^{10}, n^{9}, n^{8}, n^{6}, n^{5}, n^{4}, n^{2}, n^{1}\)
15.
| a. \(3 \times 815 + 6 \times 811 + 2 \times 87\) |
| b. \(3 \times 515 + 4 \times 510 + 2 \times 57\) |
| c. \(4 \times 1114 + 3 \times 1110 + 2 \times 110\) |
| d. \(1 \times 214 + 1 \times 211 + 1 \times 24\) |
16.
| a. \(9^{6}\) | b. \(9^{0}\) | c. \(9^{12}\) | d. \(9^{10}\) |
17.
| a. \(2401000300_{\text{five}}\) |
| b. \(30040001600_{\text{eight}}\) |
| c. \(7000804000_{\text{twelve}}\) |
| d. \(201010200_{\text{three}}\) |
18.
| a. \(6^{17}\) | b. \(9^{19}\) |
19. 3: 0, 1, 2
20. 4: 0, 1, 2, 3
21. 5: 0, 1, 2, 3, 4
22. 6: 0, 1, 2, 3, 4, 5
23. 8: 0, 1, 2, 3, 4, 5, 6, 7
24. No, because the only digits that can occur in a Base Seven numeral are 0, 1, 2, 3, 4, 5 and 6.
25.
| a. Seven |
| b. There is no highest base, it can occur in any base higher than Six. |
26. 11
27. 12
28. 13
29.
| a. 671 | b. 1291 | c. 1830 |
| d. 3496 | e. 1358 | f. 2231 |
30.
| a. 6 | b. 12 | c. 20 | d. 30 |
| e. 42 | f. 56 | g. 72 | h. 90 |
| i. 132 | j. 156 | k. 182 | l. 420 |
31. \(13201154320050146_{\text{eleven}}\) is larger. Exercise 30 illustrates that if two numerals have the same exact digits, the one with the higher base has a higher value since each place value is worth more. Explanations may vary.
32. \(4 \times 1213 + 10 \times 129 + 11 \times 123\)
33. \(600T000E0000W00_{\text{thirteen}}\)
Exercise Set 4 Solutions
1. Ask a friend how your art work is.
2.
| a. 4, 4, 4, 4, 4, 4 |
| b. 4,16,64,256 |
| c. 5 |
| d. 36 |
3. 2, 2, 2, 2, 2
4. 3, 3, 3
5. 4, 4, 4
6.a.
|
i. 42 ii. 21, 0 iii. 10, 1, 0 iv. 5, 0, 1, 0 v. 2, 1, 0, 1, 0 vi. 1, 0, 1, 0, 1, 0 vii. See first row of part d. |
| b. See second row of part d. |
| c. See third row of part d. |
|
d. 101010 Base Two 001120 Base Three 000222 Base Four |
7.
| a. \(110100_{\text{two}}\) |
| b. \(1221_{\text{three}}\) |
| c. \(310_{\text{four}}\) |
8.
| a. \(3020_{\text{four}}\) |
| b. \(1212_{\text{seven}}\) |
| c. \(1011001_{\text{two}}\) |
| d. \(100210_{\text{three}}\) |
| e. \(1E8_{\text{thirteen}}\) |
9.
| a. \(12202_{\text{three}}\) |
| b. \(10E_{\text{twelve}}\) |
| c. \(10011011_{\text{two}}\) |
| d. \(1110_{\text{five}}\) |
10.
| a. \(T23T_{\text{eleven}}\) |
| b. \(625T_{\text{thirteen}}\) |
11.
| a. \(59T_{\text{twelve}}\) |
| b. \(1506_{\text{eight}}\) |
| c. \(2305_{\text{seven}}\) |
| d. \(1131_{\text{nine}}\) |
13. 10
14. The last digit of the previous numeral must have been a 9 and the last digit of the new numeral will be 0.
15. 99,999,999
16. 1,000,000,000
17. 3
18. The last digit of the previous numeral must have been a 2 and the last digit of the new numeral will be 0.
19. \(1000000_{\text{three}}\)
20. \(2222222_{\text{three}}\)
21.
| a. \(1202011_{\text{three}}\) |
| b. \(2220012_{\text{three}}\) |
| c. \(1010110_{\text{three}}\) |
| d. \(2100220_{\text{three}}\) |
| e. \(2121000_{\text{three}}\) |
22.
| a. \(1200101_{\text{three}}\) |
| b. \(1202220_{\text{three}}\) |
| c. \(2110012_{\text{three}}\) |
| d. \(2110022_{\text{three}}\) |
23. The digit "3" can't be in the numeral.
24. \(0_{\text{four}}, 1_{\text{four}}, 2_{\text{four}}, 3_{\text{four}}, 10_{\text{four}}, 11_{\text{four}}, 12_{\text{four}}, 13_{\text{four}}, 20_{\text{four}}, 21_{\text{four}}, 22_{\text{four}}, 23_{\text{four}}, 30_{\text{four}}, 31_{\text{four}}, 32_{\text{four}}, 33_{\text{four}}, 100_{\text{four}}, 101_{\text{four}}, 102_{\text{four}}, 103_{\text{four}}, 110_{\text{four}}, 111_{\text{four}}, 112_{\text{four}}, 113_{\text{four}}\)
25. 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001, 10010, 10011, 10100
26. 75, 76, 77, 100, 101, 102, 103, 104
27.
| a. \(3026_{\text{eight}}, 3030_{\text{eight}}\) |
| b. \(1234_{\text{five}}, 1241_{\text{five}}\) |
| c. \(101011_{\text{two}}, 101101_{\text{two}}\) |
28.
| a. \(12221_{\text{three}}\), 160 |
| b. \(2405_{\text{eight}}\), 1285 |
| c. \(1310_{\text{three}}\), 205 |
Exercise Set 5 Solutions
1.
| a. \(\frac{1}{4}\) | b. \(\frac{1}{16}\) | c. \(\frac{1}{64}\) |
| d. \(\frac{1}{3}\) | e. \(\frac{1}{25}\) | f. \(\frac{1}{8}\) |
2.
| a. 35\(\frac{1}{4}\) | b. 168\(\frac{7}{11}\) |
| c. 15\(\frac{1}{2}\) | d. 27\(\frac{1}{2}\) |
3.
| a. 27\(\frac{13}{36}\) | b. 45\(\frac{27}{64}\) |
| c. 90\(\frac{9}{49}\) | d. 7\(\frac{5}{8}\) |
| e. 26\(\frac{26}{27}\) | f. 1475\(\frac{5}{72}\) |
4.
| a. binary: 00110101; decimal: 53 |
| b. binary: 10011010; decimal: 154 |
| c. binary: 01010100; decimal: 84 |
| d. binary: 00000000; decimal: 0 |
| e. binary: 11111111; decimal: 255 |
5.
| a. binary: 00110101; hex: 35 |
| b. binary: 10011010; hex: 9A |
| c. binary: 01010100; hex: 54 |
| d. binary: 00000000; hex: 00 |
| e. binary: 11111111; hex: FF |
6.
| a. binary: 01011110; decimal: 94 |
| b. binary: 11100101; decimal: 229 |
| c. binary: 00111001; decimal: 57 |
| d. binary: 00011111; decimal: 31 |
| e. binary: 10011000; decimal: 152 |
| f. binary: 00101010; decimal: 42 |
| g. binary: 00000111; decimal: 7 |
| h. binary: 01000000; decimal: 64 |
7.
| a. I LOVE MATH! |
| b. TEACHING IS A CHALLENGING, BUT REWARDING CAREER! |
8.
|
a. Hex: 48, 45, 4C, 50, 21 Binary: 01001000,01000101, 01001100, 01010000, 00100001 |
|
b. Hex: 2,45,20,48,41,50,50,59,2E Binary: 01000010, 01000101,00100000,01001000,01000001,01010000, 01010000, 01011001, 00101110 |
| c. This will depend on your name! |
9.
| a. binary: \(1001001_{\text{two}}\) hex: \(49_{\text{sixteen}}\) |
| b. binary: \(1111010_{\text{two}}\) hex: \(7A_{\text{sixteen}}\) |
| c. binary: \(110010_{\text{two}}\) hex: \(32_{\text{sixteen}}\) |
| d. binary: \(11111010_{\text{two}}\) hex: \(FA_{\text{sixteen}}\) |
| e. binary: \(1111101000_{\text{two}}\) hex: \(3E8_{\text{sixteen}}\) |
Homework Solutions
1. b. There is no matching possible because the cardinality of the two sets is different
2. One possibility is: \(1 \leftrightarrow 5, 2 \leftrightarrow 10, 3 \leftrightarrow 15, 4 \leftrightarrow 20\), etc. Give your own answer
3.
(1) \(SBC \leftrightarrow SRC, SBT \leftrightarrow SRT, SBQ \leftrightarrow SRQ\)
(2) \(SBC\leftrightarrow SRC, SBT \leftrightarrow SRQ, SBQ \leftrightarrow SRT\)
(3) \(SBC \leftrightarrow SRT, SBT \leftrightarrow SRC, SBQ \leftrightarrow SRQ\)
(4) \(SBC \leftrightarrow SRT, SBT \leftrightarrow SRQ, SBQ \leftrightarrow SRC\)
(5) \(SBC \leftrightarrow SRQ, SBT \leftrightarrow SRT, SBQ \leftrightarrow SRC\)
(6) \(SBC \leftrightarrow SRQ, SBT \leftrightarrow SRC, SBQ \leftrightarrow SRT\)
4.
| a. 16 |
| c. 1962 |
| d. 744 |
| f. 3,031,020 |
| h. 50,703 |
| i. 1395 |
| k. 971 |
5.
| a. CCCXLII |
|
c.  |
|
e.  |
6.
| a. \(59T_{\text{twelve}}\) |
d.  |
7. \(7T4E_{\text{twelve}}\)
10. a. \(17342575T_{\text{eleven}}\)
11. a. \(539100E0_{\text{twelve}}\)
13.
| a. \(10122_{\text{three}}\) | b. 98 |
14.
| a. \(300640000_{\text{seven}}\) | c. \(40T00E00_{\text{thirteen}}\) |
15.
| a. \(2 \times 911 + 5 \times 97 + 3 \times 94\) | c. \(8 \times 1210 + 11 \times 125 + 10 \times 123\) |
16.
| a. \(39\frac{1}{3}\) | b. \(16\frac{7}{9}\) |
18.
| a. \(302.301_{\text{four}}\) | c. \(101.1001_{\text{two}}\) |
Module 3 Addition and Subtraction
Exercise Set 1 Solutions
1.
| b. 3 | d. 4 | f. 7 |
2.
| a. {t, u, v, w, x, y, z} | b. 7 | c. no | d. no | e. A & B must have no elements in common. |
4.
| a. {LBT, LBC, LBQ, LRT, LRC, LRQ,LGT, LGQ, LGC, LYT, LYC, LYQ, SBT, SRT, SGT, SYT} | b. 16 | c. no | d. L and T have elements in common. |
5.
|
a. Let A = {x, y} and B = {a, b, c, d} 2+4 = n(A) + n(B) = \(n(A \cup B)\) = n({x, y, a, b, c, d}) = 6 Therefore, 2 + 6 = 6 |
Since n(A) = 2, n(B) =4, and \(A \cap B =Ø\), then by substituting n(A) for 2 and n(B) for 4 by substituting n(A) for 2 and n(B) for 4 by computing \(A \cup B\) by counting the elements in \(A \cup B\) |
|
b. Let A = {x, y} and B = {a, b} 2+2 = n(A)+n(B) = \(n(A \cup B)\) = n({x, y, a, b}) = 4 Therefore, 2 + 2 = 4 |
Since n(A) = 2, n(B) =2, and \(A \cap B = Ø\), then by substituting n(A) for 2 and n(B) for 2 by the set theory definition of addition by computing \(A \cup B\) by counting the elements in \(A \cup B\) |
|
c. Let A = {x, y, z} and B = { } 3 + 0 = n(A) + n(B) = \(n(A \cup B)\) = n({x, y, z}) = 3 Therefore, 3 + 0 = 3 |
Since n(A) = 3, n(B) =0, and \(A \cap B = Ø\), then by substituting n(A) for 3 and n(B) for 0 by the set theory definition of addition by computing \(A \cup B\) by counting the elements in \(A \cup B\) |
6.
| a. K | b. H | c. B | d. O | e. S |
| f. P | g. B | h. N | i. H | j. B |
| k. N | l. H | m. each pair is equal. |
8.
| a. Y, B | b. D, B | c. same | d. B, S | e. D, S | f. same |
11.
| a. Commutative property of addition |
| b. Commutative property of addition |
| c. Associative property of addition |
| d. Associative property of addition |
13. W + W + W, W + R, R + W, L
14. 1 + 1 + 1 = 3, 1 + 2 = 3, 2 + 1 = 3, 3 = 3
15. P,W + W + W + W, W + W + R, W + R + W, R + W + W, W + L, L + W, R + R
16. 4 = 4, 1 + 1 + 1 + 1 = 4, 1 + 3 = 4, 3 + 1 = 4, 2 + 2 = 4, 1 + 1 + 2 = 4, 1 + 2 + 1 = 4, 2 + 1 + 1 = 4
17. There are eleven trains: R + P, L+ L, R + R + R, W + W + W + L, D, W + W + W + W + W + W, W + Y, W + W + W + W + R, W + L + R, W + W + P, W + W + R + R
18. 1 + 1 + 1 + 1 + 1 + 1 = 6, 1 + 5 = 6, 1 + 1 + 4 = 6, 1 + 1 + 1 + 1 + 2 = 6, 1 + 1 + 2 + 2 = 6, 1 + 1 + 1 + 3 = 6, 6 = 6, 2 + 2 + 2 = 6, 1 + 2 + 3 = 6, 3 + 3 = 6, 2 + 4 = 6
19.
| a. R | b. Y | c. N |
| d. R | e. P | f. W |
20.
| b. because 30 = 22 + 8 |
| c. because 156 = 96 + 60 |
| d. because 80 = 0 + 80 |
| e. because 231 = 195 + 36 |
| f. because 987 = 967 + 20 |
21.
| b. because 30 + 69 = 99 |
| c. because 19 + 51 = 70 |
| d. because 0 + 32 = 32 |
| e. because 489 + 11 = 500 |
| f. because 65 + 136 = 201 |
22.
| a. left | b. right |
23. yes
24. yes
25.
| a. < | b. > |
26. {0, 1, 2, 3, . . .}
27. yes
28. no
29.
| a. closed (since 0 + 0 = 0) |
| b. not closed; 1 + 1 = 2 is a counterexample |
| c. closed; mult of 2: proof is left to you! |
| d. not closed; 1 + 3 = 4 is a counterexample |
Exercise Set 2 Solutions
1.
|
a.  |
|
b.  |
|
c.  |
|
d.  |
2.
| a. B | b. D | c. G |
3.
| a. DDDCCCCCCAAAAA |
| b. EEEDCCCCCBBAAAAA |
| c. FEB |
| d. E |
4.
|
a.  |
b.  |
c.  |
5.
|
a.  |
b.  |
c.  |
|
d.  |
e.  |
6. \(33_{\text{four}} + 31_{\text{four}} = 130_{\text{four}}\)
7. \(21_{\text{seven}} + 16_{\text{seven}} = 40_{\text{seven}}\)
8. \(1111_{\text{two} + 1101_{\text{two} = 11100_{\text{two}}\)
9. \(16_{\text{nine}} + 14_{\text{nine}} = 31_{\text{nine}}\)
10. \(120_{\text{three}} + 111_{\text{three}} = 1001_{\text{three}}\)
11. \(17_{\text{eight}} + 15_{\text{eight}} = 34_{\text{eight}}\)
13.
| a. \(2_{\text{nine}}\) | b. \(2_{\text{seven}}\) | c. \(T_{\text{twelve}}\) |
| d. \(8_{\text{eleven}}\) | e. \(4_{\text{six}}\) | f. \(1_{\text{two}}\) |
| g. \(1_{\text{three}}\) | h. \(3_{\text{four}}\) | i. \(2_{\text{five}}\) |
14.
| a. \(14_{\text{eleven}}\) | b. \(12_{\text{five}}\) |
| c. \(11_{\text{eight}}\) | d. \(11_{\text{thirteen}}\) |
| e. \(12_{\text{four}}\) | f. \(13_{\text{seven}}\) |
| g. \(11_{\text{three}}\) | h. \(10_{\text{two}}\) |
| i. \(12_{\text{six}}\) | j. \(13_{\text{nine}}\) |
15.
|
a. Base Three Addition Table  |
|
b. Base Six Addition Table  |
|
c. Base Two Addition Table  |
Exercise Set 3 Solutions
1.
| a. 50 | b. 51 | c. 47 | d. 52 |
2.
| a. 69 | b. 70 | c. 74 |
3.
| a. 47 | b. 43 | c. 53 | d. 53 |
4.
| a. \(1065_{\text{thirteen}}\) | b. \(10110_{\text{two}}\) |
| c. \(12222_{\text{five}}\) | d. \(1168_{\text{nine}}\) |
| e. \(110100_{\text{two}}\) | f. \(10211_{\text{three}}\) |
| g. \(T450_{\text{twelve}}\) | h. \(11521_{\text{seven}}\) |
6.
|
a. 43 + 47 = (40 + 3) + (40 + 7) = (40 + 40) + (3 + 7) = 80 + 10 = 90 |
|
b. 88 + 54 = (80 + 8) + (50 + 4) = (80 + 50) + (8 + 4) = 130 + 12 = 100 + 30 + 10 + 2 = 100 + 40 + 2 = 142 |
7. The first student adds the ones (9 + 7 = 16), then the tens (50 + 60 = 110) and thirdly, the hundreds (800 + 400 = 1200). Next those three intermediate sums are added together (16 + 110 + 1200 = 1326). The second student is doing basically the same thing except the hundreds are added first, then the tens and ones are added. The first student is adding right to left whereas the second student is adding left to right.
9.
| a. 12,109 | b. 111,463 |
| c. 16,668 | d. 128,334 |
10.
| a. 8,805 | b. 10,463 |
| c. 13,029 | d. 106,003 |
11.
| a. \(1300_{\text{six}}\) | b. \(1392_{\text{eleven}}\) |
| c. \(1166_{\text{eight}}\) | d. \(11001_{\text{two}}\) |
| e. \(3201_{\text{five}}\) | f. \(1065_{\text{thirteen}}\) |
| g. \(10110_{\text{two}}\) | h. \(12222_{\text{five}}\) |
| i. \(1168_{\text{nine}}\) | j. \(110100_{\text{two}}\) |
| k. \(10211_{\text{three}}\) | l. \(T450_{\text{twelve}}\) |
| m. \(11521_{\text{seven}}\) |
12.
| a. seven |
| b. thirteen |
| c. twelve |
| d. three - thirteen |
| e. four - thirteen |
13.
| a. Base Eight; \(132_{\text{eight}}\) |
| b. Base Nine: \(82_{\text{nine}}\) |
| c. Base Three; \(110_{\text{three}}\) |
| d. Base Ten; 123 |
14. She thought of 68 as 70 - 2. So, 47 + (70 - 2) = (47 + 70) - 2 = 117 - 2 = 15
15. First, he added the tens together, (40 + 60 = 100), then he added the ones together (8 + 7 = 15) and finally he added the two preliminary sums together (100 + 15 = 115).
18. 1115; LATTICE SHOWN BELOW

19.
|
a. \(41_{\text{six}}\) 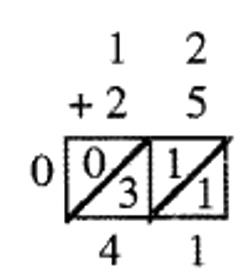 |
b. \(WOE_{\text{thirteen}}\)  |
20. Estimate: $46; Actual Sum: $45.18
22. You'll underestimate if you happen to round down on almost every item. You'll overestimate if you happen to round up on almost every item.
Exercise Set 4 Solutions
2.
| a. 7 | b. 3 | c. 4 |
4.
|
a. Let A = {t, u, v, w, x, y, z} and B = {w, y, z}. Since n(A) = 7, n(B) = 3 and \(B \subseteq A\), 7 - 3 = n(A) - n(B) by substituting n(A) for 7 and n(B) for 3 = n(A \ B) by the set theory definition of substitution = n({t, u, v, x}) by computing A \ B = 4 by counting the elements in A \ B Therefore, 7 - 3 = 4. |
|
a. Let A = {t, u, v, w, x, y, z} and B = {w, y, z}. Since n(A) = 7, n(B) = 3 and \(B \subseteq A\), 7 - 3 = n(A) - n(B) by substituting n(A) for 7 and n(B) for 3 = n(A \ B) by the set theory definition of substitution = n({t, u, v, x}) by computing A \ B = 4 by counting the elements in A \ B Therefore, 7 - 3 = 4. |
|
a. Let A = {t, u, v, w, x, y, z} and B = {w, y, z}. Since n(A) = 7, n(B) = 3 and \(B \subseteq A\), 7 - 3 = n(A) - n(B) by substituting n(A) for 7 and n(B) for 3 = n(A \ B) by the set theory definition of substitution = n({t, u, v, x}) by computing A \ B = 4 by counting the elements in A \ B Therefore, 7 - 3 = 4. |
5.
|
a.  |
b.  |
6.

7.
|
a.  |
b.  |
|
c.  |
d.  |
8.
| \(32_{\text{five}}; 14_{\text{five}}; 13_{\text{five}}\) \(32_{\text{five}} – 14_{\text{five}} = 13_{\text{five}}\) |
9.
| \(21_{\text{eight}}; 7_{\text{eight}}; 12_{\text{eight}}\) \(21_{\text{eight}} – 7_{\text{eight}} = 12_{\text{eight}}\) |
10.
| \(210_{\text{three}}; 21_{\text{three}}; 112_{\text{three}}\) \(210_{\text{three}} – 21_{\text{three}} = 112_{\text{three}}\) |
12. L
13.
| a. B | b. Y | c. N | d. N | e. S |
14. This is done with the C-Strips.
15. No; 7 –10 is not a whole number
16.
| a. closed | b. not closed; 2-4 is a counterexample |
17.
| a. 12 – 4 = 8 ; 12 – 8 = 4 |
| b. 170 – 130 = 40 ; 170 – 40 = 130 |
| c. 80 – 62 = 18 ; 80 – 18 = 62 |
18.
| a. 4 = 7 –3 | b. 8 = 9 –1 |
19. No. 4 < 7 but it isn't true that 7 < 4
21.
| a. 2; 9 = 7 + 2 | b. 7; 13 = 6 + 7 |
| c. 80; 88 = 8 + 80 | d. 56; 70 = 14 + 56 |
22. \(41_{\text{five}}\)
23. \(1_{\text{two}}\)
24. \(4E_{\text{twelve}}\)
25.
| a. -5 | b. 3 |
26.
|
a. 6  |
|
b. 7  |
|
c. 5  |
|
d. 2  |
|
e. -7  |
|
f. -3  |
|
g. -12  |
|
h. 0  |
27. vector a: 6; vector c: -5; vector d: 3
Exercise Set 5 Solutions
1.
| a. \(314_{\text{thirteen}}\) | b. \(151_{\text{nine}}\) |
| c. \(1225_{\text{six}}\) | d. \(134_{\text{five}}\) |
| e. \(12_{\text{three}}\) |
2.
| a. 1618 | b. \(31_{\text{four}}\) |
| c. \(363_{\text{twelve}}\) | d. \(45_{\text{six}}\) |
| e. \(111_{\text{two}}\) | f. \(254_{\text{nine}}\) |
| g. \(33_{\text{five}}\) | h. \(234_{\text{seven}}\) |
| i. \(2_{\text{three}}\) | j. \(236_{\text{eight}}\) |
3. Show the check by adding the answer to the subtrahend and making sure the sum is the minuend.
4.
| a. 6717 | b. \(1214_{\text{five}}\) |
| c. \(1424_{\text{eight}}\) | d. \(49E_{\text{thirteen}}\) |
| e. \(1010_{\text{two}}\) |
5. Show the check by adding the difference (answer) to the subtrahend and making sure the sum is the minuend.
6.
| a. 6697 | b. \(1144_{\text{five}}\) |
| c. \(1774_{\text{eight}}\) | d. \(4WE_{\text{thirteen}}\) |
| e. \(111_{\text{two}}\) |
7. Show the check by adding the difference (answer) to the subtrahend and making sure the sum is the minuend.
10.
| a. 9462 | b. \(122_{\text{four}}\) | c. \(101_{\text{two}}\) |
11. \(1_{\text{two}}\)
12.
| a. 4677 | b. \(134_{\text{five}}\) |
13.
| a. Since the minuend is \(120_{\text{three}}\), the next place value block is a base three block. Since the subtrahend is \(12_{\text{three}}\), we have to figure out what to add to \(12_{\text{three}}\) to make a block. \(12_{\text{three}}\) is a long and two units, so I have to add 1 unit, 1 long and 2 flats to make a block. Therefore, ass 2 flats, a long a unit to the minuend, \(120_{\text{three}}\), which gives 1 block, 1 flat and 1 unit for the new minuend. If I remove the largest block from this new minuend, I should have the answer of 1 flat and 1 unit.So the answer is \(101_{\text{three}}\). I've left the drawing up to you. See #13 below to see how to start the problem with an abbreviated drawing. |
|
b. Since the minuend is \(213_{\text{four}}\), the next place value block is a base four block. Since the subtrahend is \(133_{\text{four}}\), we have to figure out what to add to \(133_{\text{four}}\) to make a block. \(133_{\text{four}}\) is a flat, 3 longs and three units, so I have to add 1 unit and 2 flats to make a block. Therefore, add 2 flats and a unit to the minuend, \(213_{\text{four}}\), which gives 1 block and 2 longs for the new minuend. If I remove the largest block from this new minuend, I should have the answer of 2 longs. So the answer is \(20_{\text{four}}\). You can use abbreviations for the drawing and start by representing each original number as shown below. I've left the part to add on and final subtraction for you  |
14.
| a. She is breaking up the subtrahend into three parts (100 + 50 + 2), subtracting one place value at a time. 634 – 100 = 534; 534 – 50 = 484; 484 – 2 =482. |
| b. He is using a complementary method. If you add 48 to 152, you get 200. So he adds 48 to the minuend (634 + 48 = 682) and then subtracts 200. |
Homework Solutions
1. Provide your own sets. Here is one solution.
a. First, we must define two sets, A and B, that are disjoint with each other, such that one set has 5 elements and the other has 3 elements.
Let A = {1, 2, 3, 4, 5} and B = {x, y, z}. Since n(A) = 5, n(B) = 3 and \(A \cap B = Ø\), we can find the sum of 5 and 3 by first forming the union of A and B and then counting the number of elements in their union. \(A \cup B\) = {1, 2, 3, 4, 5, x, y, z}. Since n(\(A \cup B\)) = 8, then 5 + 3 = 8.
2. a. since 79 = 66 + 13
3. a. closed under both operations
4.
|
a.  |
|
c.  |
5.
|
a.  |
|
c.  |
6.
| a. \(12325_{\text{six}}\) | b. \(2535_{\text{five}}\) |
13. a. 6
14.
| a. Base 9 |
| c. Bases Three through Thirteen |
Module 4 Multipication
Exercise Set 1 Solutions
1.
|
b. Step 1:  |
Step 2:  |
c. Step 3:  |
d. both trains have the same length |
2.
| a. 2 dark green | b. 6 red | c. 12, 12 | d. same length | e. \(R \times D = D \times R ; 2 \times 6 = 6 \times 2\) |
3.
| a. 7 light green | b. 3 black | c. 21, 21 | d. same length | e. \(K \times L = L \times K ; 7 \times 3 = 3 \times 7\) |
4.
| a. 12 white | b. 1 hot pink | c. 12, 12 | d. same length | e. \(H \times W = W \times H ; 12 \times 1 = 1 \times 12\) |
5.
| a. D | b. W | c. R | d. P | e. L | f. K | g. L | h. R | i. R |
6.
|
a. These are the four trains, but they may have been listed them in a different order. 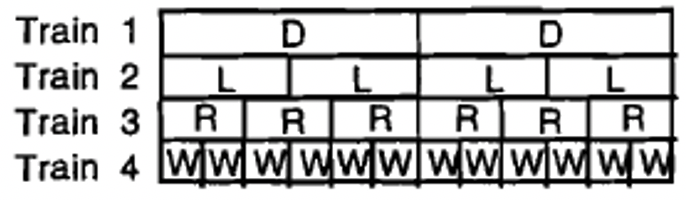 |
|
b. Using the trains as listed above, Train 1: \(R \times D = H\), or \(2 \times 6 = 12\) Train 2: \(P \times L = H\), or \(4 \times 3 = 12\) Train 3: \(D \times R = H\), or \(6 \times 2 = 12\) Train 4: \(H \times W = H\), or \(12 \times 1 = 12\) |
7. Red, R
8.
| a. 3 + 3 + 3 + 3 + 3 + 3 = 18 |
| b. 9 + 9 = 18 |
| c. 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 = 18 |
9.
| a. \(4 \times 3 = 3 + 3 + 3 + 3 = 6 + 3 + 3 = 9 + 3 = 12 ; 3 \times 4 = 4 + 4 + 4 = 8 + 4 = 12\) |
| b. \(2_{\text{five}} \times 3_{\text{five}} = 3_{\text{five}} + 3_{\text{five}} = 11_{\text{five}} ; 3_{\text{five}} \times 2_{\text{five}} = 2_{\text{five}} + 2_{\text{five}} + 2_{\text{five}} = 11_{\text{five}}\) |
10. Only the answer, and not the individual steps, are shown
|
a.  |
|
b.  |
|
c.  |
11.
|
b.  |
c. 6 |
|
e.  |
f. 6 |
| g. same length | h. (\(R \times L ) \times P) = R \times (L \times P)\) |
| i. \((2 \cdots 3) \cdots 4 = 2 \cdots (3 \cdots 4)\) | j. \((2 \cdots 3) \cdots 4 = 6 \cdots 4 = 24; 2 \cdots (3 \cdots 4) = 2 \cdots 12 = 24\) |
| k. yes |
12.
|
b.  |
c. 10 |
|
e.  |
f. 10 |
| g. same length | h. \((Y \times R ) \times L) = Y \times (R \times L)\) |
| i. \((5 \cdots 2) \cdots 3 = 5 \cdots (2 \cdots 3)\) | j. \((5 \cdots 2) \cdots 3 = 10 \cdots 3 = 30; 5 \cdots (2 \cdots 3) = 5 \cdots 6 = 30\) |
| k. yes |
13. Do the order of operations to simplify each side of each equation in a - d.
14. There are various combinations you could use for part a.
15.
| a. 3 purple strips and 3 yellow strips. | b. same as part a |
| c. \(L \times (P + Y) = (L \times P) + (L \times Y)\) | d. \(4 \times (2 + 3) = (4 \times 2) + (4 \times 3)\) |
| e. \(4 \times (2 + 3) = 4 \times 5 = 20\) and \((4 \times 2) + (4 \times 3) = 8 + 12 = 20\) |
16.
| a. 2 white strips and 2 dark green strips | b. same as part a |
| c. \(R \times (W + D) = (R \times W) + (R \times D)\) | d. \(2 \times (1 + 6) = (2 \times 1) + (2 \times 6)\) |
| e. \(2 \times (1 + 6) = 2 \times 7 = 14\) and \((2 \times 1) + (2 \times 6) = 2 + 12 = 14\) |
17. Do the order of operations to simplify each side of each equation in a - d.
18. There are various combinations you could use for part a and b.
19.
| a. R; \(1 \cdots 2 = 2\) | b. B; \(1 \cdots 9 = 9\) | c. D; \(1 \cdots 6 = 6\) |
| d. S; \(1 \cdots 11 = 11\) | e. N; \(8 \cdots 1 = 8\) | f. H; \(12 \cdots 1 = 12\) |
20. W, W
21.
| a. \(764 \cdots (1000 - 1) = 764 \cdots 1000 - 764 \cdots 1 = 764000 - 764 = 763236\) |
| b. \(324 \cdots (100 + 2) = 324 \cdots 100 + 324 \cdots 2 = 32400 + 648 = 33048\) |
| c. \(83 \cdots (74 + 26) = 83 \cdots 100 = 8300\) |
22. Make sure you know all the properties and can provide examples.
23.
| a. {(3,2), (3,6), (4,2), (4,6)} |
| b. {(6,5), (7,5),(8,5),(9,5)} |
| c. { } |
| d. {(a,a)} |
| e. {(x,x), (x,y), (y,x), (y,y)} |
| f. {(1,1), (1,3), (1,5), (3,1), (3,3), (3,5), (5,1), (5,3), (5,5)} |
24. a. Any two sets, one having 5 elements and one having 2 elements can be used. This is just one possible solution. Let M = {a,b,c,d,e} and let N = {x,y}. Since n(M) = 5 and n(N) = 2, then \(5 \times 2 = n(M \times N) = n({(a,x), (a,y), (b,x), (b,y), (c,x), (c,y), (d,x), (d,y), (e,x), (e,y)}) = 10\).
25.
| a. \(8 \times 6\) | b. \(3 \times 10\) | c. \(8 \times 6\) | d. \(5 \times 5\) | e. \(4 \times 14\) | f. \(3 \times 7\) |
28. c. \(6 \times 4\)
30.
|
a.  |
b.  |
c.  |
d.  |
e. yes |
31. The distributive property of multiplication over addition.
32. This should be done like exercise 30. Explain the steps as well as show the pictures.
33.
| a. 8 | b. 8 | c. same length |
Exercise Set 2 Solutions
2.
|
\(13 \times 29\) 1 -----> 29 2 -----> 58 4 ----->116 8 ----->232 ---------------------------- 232 + 116 + 29 = 377 |
\(29 \times 13\) 1 ----->13 2 ----->26 4 ----->52 8 ----->104 16 ----->208 ---------------------------- 208 + 104 + 52 + 13 = 377 |
3.
|
\(27 \times 14\) 1 -----> 14 2 -----> 28 4 -----> 56 8 -----> 112 16 -----> 224 ---------------------------- 224 + 112 + 28 + 14 = 378 |
\(14 \times 27\) 1 -----> 27 2 ----->54 4 ----->108 8 ----->216 ---------------------------- 216 + 108 + 54 = 378 |
4.
5.
|
a. Answer: 3,591  |
b. Answer: 29,070  |
e. Answer: 3,886  |
f.  |
6.
| a. \(221_{\text{four}}\) |
b.  |
| c. \(1102_{\text{four}}\) | d. \(2_{\text{four}} \times 221_{\text{four}} = 1102_{\text{four}}\) |
7.
| a. \(221_{\text{four}}\) |
b.  |
| c. \(1102_{\text{four}}\) | d. \(2_{\text{four}} \times 221_{\text{four}} = 1102_{\text{four}}\) |
8. Make two piles of base three blocks, each having 2 flats, 2 longs and a unit. The two equal piles are shown below.

Then, combine the piles together and make appropriate exchanges. After making exchanges, this is what it looks like:

Write the base three numeral represented after making all exchanges. The answer is \(1212_{\text{three}}\).
9. Make three piles of base three blocks, each having 2 flats, 2 longs and a unit. The three equal piles are shown below.

Then, combine the piles together and make appropriate exchanges. After making exchanges, this is what it looks like:

Write the base three numeral represented after making all exchanges. The answer is \(2210_{\text{three}}\).
10.
| a. a flat | b. a flat | c. a flat | d. \(L \times L\) = F |
11.
| a. a block | a. a block | a. a block | d. \(F \times L\) = B |
12.
| a. a long block | a. a long block | a. a long block | d. \(B \times L\) = LB |
13.
| a. F | b. B | c. LB | d. B | e. LB |
15.
| a. 3, 1 and 2 | b. 3 blocks, 1 flat and 2 longs |
16. Only the answers are given here. Make sure you show it with blocks and EXPLAIN.
| a. \(1032_{\text{four}}\) | b. \(10122_{\text{three}}\) |
17.
| a. a long block | b. a long block | c. a long block | d. \(F \times F\) = LB |
18.
| a. U | b. L | c. F | d. B |
| e. L | f. F | g. B | h. F |
| i. B | j. LB |
20. The answer is \(20010_{\text{three}}\). Make sure you show it with blocks and EXPLAIN.
21. The entire table is shown:

22.
|
a. \(23_{\text{five}} \times 32_{\text{five}}\) = (2L + 3U) \(\times\) (3L + 2U) = \(2L \times 3L + 2L \times 2U + 3U \times 3L + 3U \times 2U\) = 6F + 4L + 9L + 6U = 6F + 13L + 6U = 1B + 1F + 2F + 3L + 1L + 1U = 1B + 3F + 4L + 1U = \(1341_{\text{five}}\) |
|
\(42_{text{eight}} \times 53_{\text{eight}}\) = (4L + 2U) \(\times\) (5L + 3U) = \(4L \times 5L + 4L \times 3U + 2U \times 5L + 2U \times 3U\) = 20F + 12L + 10L + 6U = 20F + 22L + 6U = 2B + 4F + 2F + 6L + 6U = 2B + 6F + 6L + 6U = \(2666_{\text{eight}}\) |
23.
\(212_{\text{four}} \times 102_{\text{four}}\)
= (2F + 1L + 2U) \(\times\) (1F + 2U)
= \(2F \times 1F + 2F \times 2U + 1L \times 1F + 1L \times 2U + 2U \times 1F + 2U \times 2U\)
= 2LB + 4F + 1B + 2L + 2F + 4U
= 2LB + 1B + 6F + 2L + 4U
= 2LB + 1B + 1B + 2F + 2L + 1 L
= 2LB + 2B + 2F + 3L
= \(22230_{\text{four}}\)
24.
|
a. \(361_{\text{nine}} \times 15_{\text{nine}}\) = (3F + 6L + 1U) \(\times\) (1L + 5U) = \(3F \times 1L + 3F \times 5U + 6L \times 1L + 6L \times 5U + 1U \times 1L + 1U \times 5U\) = 3B + 15F + 6F + 30L + 1L + 5U = 3B + 21F + 31L + 5U = 3B + 2B + 3F + 3F + 4L + 5U = 5B + 6F + 4L + 5U = \(5645_{\text{nine}}\) |
|
b. \(111_{\text{two}} \times 11_{\text{two}}\) = (1F + 1L + 1U) \(\times\) (1L + 1U) = \(1F \times 1L + 1F \times 1U + 1L \times 1L + 1L \times 1U + 1U \times 1L + 1U \times 1U\) = 1B + 1F + 1F + 1L + 1L + 1U = 1B + 2F + 2L + 1U = 1B + 1B + 1F + 1U = 1LB + 1F + 1U = \(10101_{\text{two}}\) |
25.
|
a. Answer: \(1422_{\text{six}}\)  |
b. Answer: \(1469_{\text{eleven}}\)  |
c. \(100011_{\text{two}}\) |
| d. \(T09_{\text{twelve}}\) | e. \(20211_{\text{three}}\) | f. \(2122_{\text{four}}\) |
26. Only a, b and c are shown here. Make sure you do d and e.
 |
 |
 |
27.
| a. \(1103_{\text{five}}\) | b. \(1T58_{\text{thirteen}}\) | c. \(1022_{\text{three}}\) |
| d. \(16015_{\text{seven}}\) | e. \(16015_{\text{seven}}\) | f. \(101310_{\text{four}}\) |
29. \(2144_{\text{five}}\)
30. \(31653_{\text{seven}}\)
31. \(10001111_{\text{two}}\)
32. \(1220212_{\text{three}}\)
33. \(15417_{\text{twelve}}\)
34. \(115503_{\text{six}}\)
35. \(2012220_{\text{three}}\)
36. \(424204_{\text{six}}\)
37. \(101001010_{\text{two}}\)
38. \(T73E8_{\text{twelve}}\)
39. \(615032_{\text{eight}}\)
40. \(1033230_{\text{four}}\)
41. \(2321411_{\text{five}}\)
42. \(1563526_{\text{seven}}\)
43. \(414025_{\text{nine}}\)
44. \(8T6697_{\text{eleven}}\)
Homework Solutions
1. a. 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 32
3. a. P; \(4 \cdots 1 = 4\)
4. a. {(3,0), (3,1), (3,6), (x,0), (x,1), (x,6)}
6.
| a. B | c. LB | e. FB |
10.
a. Associative Property of Multiplication
Illustrate this equation is true: \((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}\))
Left side: \((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 11_{\text{five}} \cdots 4_{\text{five}} = 44_{\text{five}}\)
Right side: \(2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}) = 2_{\text{five}} \cdots 22_{\text{five}}) = 44_{\text{five}}\)
Both expressions equal \(44_{\text{five}}\), so \((2_{\text{five}} \cdots 3_{\text{five}}) \cdots 4_{\text{five}} = 2_{\text{five}} \cdots (3_{\text{five}} \cdots 4_{\text{five}}\))
Distributive Property of Multiplication of Addition:
Illustrate this equation is true: \(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = (2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five)}}\)
Left side: \(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = 2_{\text{five}} \cdots (12_{\text{five}}) = 24_{\text{five}}\)
Right side: \((2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five}}) = 11_{\text{five}} + 13_{\trxt{five}} = 24_{\text{five}}\)
Both expressions equal \(24_{\text{five}}\), so \(2_{\text{five}} \cdots (3_{\text{five}} + 4_{\text{five}}) = (2_{\text{five}} \cdots 3_{\text{five}}) + (2_{\text{five}} \cdots 4_{\text{five}}\))
Module 5 Binary Operations
Exercise Set 1 Solutions
2.
| a. 16 | b. 65 | c. 2 | d. 42 | e. 4 |
| f. 18 | g. 14 | h. 41 | i. 20 |
3.
| a. m ! n = n ! m; Yes; Proof: If m ! n =n ! m, then ! is commutative. m ! n = 2 and n ! m = 2. Since both expressions (m ! n and n ! m) equal 2, then ! is commutative. |
| b. \(m \bigoplus n = n \bigoplus m\); Yes; Proof: If \(m \bogoplus n = n \bigoplus m\), then \(\bigoplus\) is commutative. \(m \bigoplus n = 3mn\) and \(n \bigoplus m = 3nm\). Since 3mn = 3nm, then \(m \bigoplus n = n \bigoplus m.\) Therefore, is commutative. |
| c. m # n = n # m; Yes; Provide your own an example using numbers. |
| d. m ʘ n = n ʘ m; Yes; Proof: If m ʘ n = n ʘ m, then ʘ is commutative. m ʘ n = 2m + 2n, and n ʘ m = 2n + 2m. Since 2m + 2n = 2n + 2m, then m ʘ n = n ʘ m. Therefore, ʘ is commutative. |
| e. \(m \XBox n = n \XBox m\); No; Provide your own counterexample using numbers. |
| f. m , n = n , m; Yes; Proof: If m , n = n , m, then , is commutative. \(m , n = m^{2} + n^{2}\) and \(n , m = n^{2} + m^{2}\). Since \(m^{2} + n^{2} = n^{2} + m^{2}\), then m , n = n , m. Therefore ,, is commutative. |
| g. m * n = n * m; No; Provide your own counterexample using numbers. |
| h. m |
4.
| a. 17 | b. 4 | c. 2 | d. 216 | e. 36 | f. 125 |
5.
| a. 270 | b. 34 | c. 27 | d. 6 | e. 6 |
| f. 629 | g. 6 | h. 4 | i. 12 |
6.
| a. (a ! b)q c = a ! (b! c); yes; Proof: If (a ! b) ! c = a ! (b! c), then ! is associative. (a ! b) !c = 2! c = 2, and a ! (b! c) = a ! 2 = 2. Since both (a ! b) ! c and a ! (b! c) are equal to 2, then ! is associative. |
| b. \((a \bigoplus b) \bigoplus c = a \bigoplus (b \bioplus c)\); yes; Proof: If \((a \bigoplus b)r c = a \bigoplus (b \bigoplus c)\), then \(\bigoplus\) is associative. \((a \bigoplus b) \bigoplus c = 3ab \bigoplus c = 3 \cdots 3ab \cdots c = 9abc,\) and \(a \bigoplus (b \bigoplus c) = a \bigoplus 3bc = 3 \cdots a \cdots 3bc = 9abc\). Since both expressions \([(a \bigoplus b) \bigoplus c\) and \(a \bigoplus (b \bigoplus c)]\) are equal to 9abc, then \(\bigoplus\) is associative. |
| c. (a # b)# c = a # (b # c); yes; Provide your own example using numbers. |
| d. (a ʘ b) ʘ c = a ʘ (b ʘ c); no; Provide your own counterexample using numbers. |
| e. \((a \XBox b) \XBox c = a \XBox (b \XBox c)\); no; Provide your own counterexample using numbers. |
| f. (a ,b) , c = a , (b, c); no; Provide your own counterexample using numbers. |
| g. (a * b)* c = a * (b * c); no; Provide your own counterexample using numbers. |
7. a @ (b + c) = (a @ b) + (a @ c)
8. a + (b @ c) = (a + b) @ (a + c)
9.
| a. a & (b $ c) = (a & b) $ (a & c) |
| b. a $ (b & c) = (a $ b) & (a $ c) |
10.
| a. a ! (b r c) = (a ! b) r (a ! c) |
| b. no |
| c. Provide your own counterexample using numbers. |
| d. \(a \bigoplus (b ! c) = (a \bigoplus b) ! (a \bigoplus c)\) |
| e. no |
| f. Provide your own counterexample using numbers. |
11.
| a. \(a + (b \cdots c) = (a + b) \cdots (a + c)\) |
| b. no |
| c. Provide your own counterexample using numbers. |
12.
| a. \(a \cdots (b \cdots c) = (a \cdots b) \cdots (a \cdots c)\) |
| b. yes |
| c. Provide your own example using numbers. |
13.
| a. a , (b @ c) = (a , b) @ (a , c) |
| b. no |
| c. Provide your own counterexample using numbers. |
| d. a @ (b , c) = (a @ b) , (a @ c) |
| e. no |
| f. Provide your own counterexample using numbers. |
14. You are on your own here. Be creative.
15.
a. m  n = n n = n  m; no; provide your own counterexample using numbers m; no; provide your own counterexample using numbers |
b. m  n = n n = n  m; yes; provide your own proof m; yes; provide your own proof |
c. (m  n) n)  x = m x = m  (n (n  x); no; provide your own counterexample using numbers x); no; provide your own counterexample using numbers |
d. (m  n) n)  x = m y (n x = m y (n  x); no; provide your own counterexample x); no; provide your own counterexample |
e. a  (b + c) = (a (b + c) = (a  b) + (a b) + (a  c); no; provide your own counterexample c); no; provide your own counterexample |
f. a  (b + c) = (a (b + c) = (a  b) + (a b) + (a  c); no; provide your own counterexample c); no; provide your own counterexample |
g. a  (b y c) = (a (b y c) = (a  b) y (a b) y (a  c); no; provide your own counterexample c); no; provide your own counterexample |
h. a  (b (b  c) = (a c) = (a  b) b)  (a (a  c); no; provide your own counterexample c); no; provide your own counterexample |
16. \((a + b) \cdots c = (a \cdots c) + (b \cdots c)\); yes; provide your own example
17. \((a \cdots b) + c = (a + c) \cdots (b + c)\); no; provide your own counterexample
18. \((a + b) \div c = (a \div c) + (b \div c)\); yes; provide your own example
19. \(a \div (b + c) = (a \div b) + (a \div c)\); no; provide your own counterexample
20.
a. (b + c)  a = (b a = (b  a) + (c a) + (c  a); no; provide your own counterexample a); no; provide your own counterexample |
b. (b + c)  a = (b a = (b  a) + (c a) + (c  a); no; provide your own counterexample a); no; provide your own counterexample |
c. (b  c) c)  a = (b a = (b  a) a)  (c (c  a); no; provide your own counterexample a); no; provide your own counterexample |
d. (b  c) c)  a = (b a = (b  a) a)  (c (c  a); no; provide your own counterexample a); no; provide your own counterexample |
Homework Solutions
1.
| a. 23 | b. 20 | c. 2a + b | d. 26 | g. 2 |
| j. 90 | m. 1 | p. 10 | s. 26 | v. 17 |
| y. 45 |
2. a. 19
3.
| a. 20 | c. 36 | e. 21 |
Module 6 Integers
Exercise Set 1 Solutions
1. {..., -3, -2, -1}
2. {..., -3, -2, -1, 0, 1, 2, 3, ...}
3.
| a. 4 | b. 8 | c. 2 | d. 1 | e. 0 |
4.
| a. 7 | b. 13 | c. 4 | d. \(\frac{3}{7}\) | e. \(\frac{3}{7}\) | f. 6 |
5. a. 6, -6
6. a. 19, -19
7. 0
8. none
9.
| a. -5 | b. +3 |
10.
|
a. -3 since the terminal point of the last vector landed on -3.  |
|
b. -9 since the terminal point of the last vector landed on -9.  |
|
c. 4 since the terminal point of the last vector landed on 4.  |
|
d. 1 since the terminal point of the last vector landed on 1.  |
|
e. -2 since the terminal point of the last vector landed on -2.  |
|
f. -60 since the terminal point of the last vector landed on -60.  |
|
g. -1 since the terminal point of the last vector landed on -1.  |
|
h. -3 since the terminal point of the last vector landed on -3.  |
11. thermometer
12. walk two blocks east
13. The answers for these are the same as for those in exercise 10.
14.
| a. 5 | b. -9 | c. -3 | d. 6 |
15.
| a. RRRRR | b. GG | c. RRRR |
16. 0; reasons may vary
17. Answers will vary, but there will always be the same number of negative counters as positive counters in each representation.
18.
| a. -2 | b. -2 | c. -2 | d. -2 | e. -3 | f. +3 | g. +3 | h. +4 |
19. Answers will vary, but there will be 4 more positive counters than negative counters in each representation.
20. Answers will vary, but there will be 4 more negative counters than positive counters in each representation.
21.
|
a. (1) Combine 5 reds and 3 reds: RRRRR + RRR (2) There are 8 reds, RRRRRRRR, which represents -8. (3) Therefore, -5 + -3 = -8. |
|
b. (1) Combine 6 reds and 9 greens: RRRRRR + GGGGGGGGG = R R R R R R G G G G G G G G G (2) Remove 6 red-green pairs (zero), leaving GGG, which represents -3. (3) Therefore, -6 + 9 = 3. |
|
c. (1) Combine 8 reds and 6 greens: RRRRRRRR + GGGGGG = R R R R R R R R G G G G G G (2) Remove 6 red-green pairs (zero), leaving RR, which represents -2. (3) Therefore, -8 + 6 = -2. |
|
d. (1) Combine 5 reds, 3 reds and 6 greens: RRRRR + RRR + GGGGGG = R R R R R R R R G G G G G G (2) Remove 6 red-green pairs (zero), leaving RR, which represents -2. (3) Therefore, -5 + -3 + 6 = -2. |
|
e. (1) Combine 6 reds, 9 greens and 1 red: RRRRRR + GGGGGGGGG + R = R R R R R R R G G G G G G G G G (2) Remove 7 red-green pairs (zero), leaving GG which represents +2. (3) Therefore, -6 + 9 + -1 = +2. |
|
f. (1) Combine 4 greens, 6 greens and 5 reds: GGGG + GGGGGG + RRRRR = G G G G G G G G G G R R R R R (2) Remove 5 red-green pairs (zero), leaving GGGGG, which represents +5. (3) Therefore, +4 + +6 + -5 = +5. |
22.
|
a. (1) 6 – 3 means remove 3 greens from a collection of counters representing 6. (2) Represent 6 with 6 greens: GGGGGG (3) Remove 3 greens, leaving GGG, which represents +3. (4) Therefore, 6 – 3 = 3 |
|
b. (1) 4 – 6 means remove 6 greens from a collection of counters representing 4. (2) Represent 4 with 4 greens: GGGG (3) Add 2 red-green pairs (zero) to the collection: G G G G G G R R (4) Remove 6 greens, leaving RR, which represents -2. (5) Therefore, 4 – 6 = -2 |
|
c. (1) -7 – -6 means remove 6 reds from a collection of counters representing -7. (2) Represent -7 with 7 reds: RRRRRRR (3) Remove 6 reds, leaving R, which represents -1. (4) Therefore, -7 – (-6) = -1 |
|
d. (1) -3 – -7 means remove 7 reds from a collection of counters representing -3. (2) Represent -3 with 3 reds: RRR (3) Add 4 red-green pairs (zero) to the collection: R R R R R R R G G G G (4) Remove 7 reds, leaving GGGG, which represents +4. (5) Therefore, -3 – (-7) = +4 |
|
e. (1) 4 – -3 means remove 3 reds from a collection of counters representing +4. (2) Represent +4 with 4 greens: GGGG (3) Add 3 red-green pairs (zero) to the collection: G G G G G G G R R R (4) Remove 3 reds, leaving GGGGGGG, which represents +7. (5) Therefore, 4 – (-3) = +7 |
|
f. (1) -2 – 5 means remove 5 greens from a collection of counters representing -2. (2) Represent -2 with 2 reds: RR (3) Add 5 red-green pairs (zero) to the collection: R R R R R R R G G G G G (4) Remove 5 greens, leaving RRRRRRR, which represents -7. (5) Therefore, -2 – 5 = -7 |
|
g. (1) 5 – 5 means remove 5 greens from a collection of counters representing 5. (2) Represent 5 with 5 greens: GGGGG (3) Remove 5 greens, leaving nothing, which represents 0. (5) Therefore,5 – 5 = 0 |
|
h. (1) 5 – (-5) means remove 5 reds from a collection of counters representing 5. (2) Represent 5 with 5 greens: GGGGG (3) Add 5 red-green pairs (zero) to the collection: G G G G G G G G G G. R R R R R (4) Remove 5 reds, leaving GGGGGGGGGG, which represents 10. (5) Therefore, 5 – (-5) = +10 |
|
i. (1) -4 – (- 4) means remove 4 reds from a collection of counters representing -4. (2) Represent -4 with 4 reds: RRRR (3) Remove 4 reds, leaving nothing, which represents 0.. (5) Therefore, -4 – -4 = 0. |
|
j. (1) -6 – 6 means remove 6 greens from a collection of counters representing -6. (2) Represent -6 with 6 reds: RRRRRR (3) Add 6 red-green pairs (zero) to the collection: R R R R R R R R R R R R G G G G G G (4) Remove 6 greens, leaving RRRRRRRRRRRR, which represents -12. (5) Therefore, -6 – 6 = -12 |
23.
|
a. (1) 5 – 8 means remove 8 greens from a collection of counters representing 5. (2) Represent 5 with 5 greens: GGGGG (3) Add 3 red-green pairs (zero) to the collection: G G G G G G G G R R R (4) Remove 8 greens, leaving RRR, which represents -3. (5) Therefore, 5 – 8 = -3 |
|
b. (1) 5 + -8 means combine 5 greens and 8 reds: GGGGG + RRRRRRRR = G G G G G R R R R R R R R (2) Remove 5 red-green pairs (zero), leaving RRR, which represents -3. (3) Therefore, 5 + -8 = -3. |
| c. The answers are the same. |
24. There are various ways to do this problem. But in any case, the final collection for each should give the same answer.
25.
|
a. 1st way: Remove 3 greens from a collection representing -5. 2nd way: Combine a collection of 5 reds and 3 reds together. |
|
b. 1st way: Remove 8 greens from a collection representing +4. 2nd way: Combine a collection of 4 greens and 8 reds together. |
|
c. 1st way: Remove 7 reds from a collection representing -9. 2nd way: Combine a collection of 9 reds and 7 greens together. |
|
d. 1st way: Remove 10 reds from a collection representing -10. 2nd way: Combine a collection of 10 reds and 10 greens together. |
26.
| a. 4 + (-5) | b. -9 + (-7) | c. -3 + (+4) |
27.
| a. 4 + -5 + -7 + -6 + +9 | b. -43 + (+75) + 12 + 63 + (-9) |
28.
| a. -6 | b. +8 | c. negative, negative | d. positive, positive | e. opposite |
29.
| a. When the minuend and subtrahend are the same number | b. 0 |
30.
|
a. 10 – 4 = +6  |
e. 3 – 10 = -7 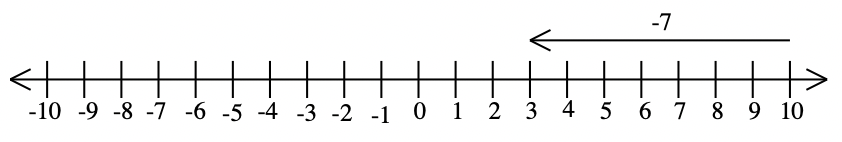 |
|
b. -7 – 5 = -12  |
f. -5 – (-8) = +3  |
|
c. 8 – (-3) = +11  |
g. 6 – (-6) = +12  |
|
d. -9 – -1 = -8  |
h. 9 – 9 = 0  |
31.
| a. 1 – (-5) = +6 | b. 13 – 10 = +3 | c. 3 – 8 = -5 |
32.
| a. -92 – -71 = -21 | d. -122 – 76 = -198 |
| b. 92 – -81 = +173 | e. 208 – 389 = -181 |
| c. -110 – -200 = +90 | a. 46 + -76 + 92 = 138 + -76 = 62 |
33.
| a. 46 + -76 + 92 = -30 + 92 = 62 |
| b. -63 + 94 + 45 + -71 = 31 + 45 + -71 = 76 + -71 = 5 |
34.
| a. 46 + -76 + 92 = 138 + -76 = 62 |
| b. -63 + 94 + 45 + -71 = 139 + -134 = 5 |
35.
| a. Closed |
| a. Closed |
| a. Closed |
| d. Not Closed; one counterexample is: 7 – 10 = -3 |
| e. Closed |
| f. Not Closed; one counterexample is: -11 – -20 = +9 |
| g. Not closed; one counterexample is: 1 + 1 = 2 |
| h. Not closed; one counterexample is: 1 – -1 = 2 |
Exercise Set 2 Solutions
1.
| a. R R R R R G |
| b. R R R R R R R R R R R R R R R G G G |
| c. RRRRRRRRRRRR = -12 |
2.
| a. R R R R R R G G |
| b. R R R R R R R R R R R R R R R R R R G G G G G G |
| c. RRRRRRRRRRRR = -12 |
3.
| a. R R R R |
| b. R R R R R R R R R R R R |
| c. -12 |
4.
| a. \(4 \times -2\) means to combine 4 sets of 2 reds: RR + RR + RR + RR = RRRRRRRR = -8 |
| b. \(3 \times 5\) means to combine 3 sets of 5 greens: GGGGG + GGGGG + GGGGG = GGGGGGGGGGGGGGG = +15 |
| c. \(5 \times -3\) means to combine 5 sets of 3 reds: RRR + RRR + RRR + RRR + RRR = RRRRRRRRRRRRRRR = -15 |
| d. \(7 \times 2\) means to combine 7 sets of 2 greens: GG + GG + GG + GG + GG + GG + GG = GGGGGGGGGGGGGG = +14 |
| e. \(0 \times -3\) means to combine 0 sets of 3 reds = 0 |
5.
| a. R R R R R R R R R R R R R R G G G G G G G G G G G G G G |
| b. R R R R R R R R R R R R R R G G |
| c. R R R R R R R R R R R R = -12 |
6.
| a. R R R R R R R R R R R R G G G G G G G G G G G G |
| b. R R R R R R R R R R R R |
| c. -12 |
7.
|
a. \(-5 \times 3\) means to remove 5 sets of 3 greens from a collection representing zero. (1) Let zero be represented by 15 reds and 15 greens: R R R R R R R R R R R R R R R G G G G G G G G G G G G G G G (2) Remove 5 sets of 3 greens from the above collection, which leaves RRRRRRRRRRRRRRR, which represents -15. Therefore, \(-5 \times 3 = -15\). |
|
b. \(-3 \times 2\) means to remove 3 sets of 2 greens from a collection representing zero. (1) Let zero be represented by 6 reds and 6 greens: R R R R R R G G G G G G (2) Remove 3 sets of 2 greens from the above collection, which leaves RRRRRR, which represents -6. Therefore, \(-3 \times 2 = -6\) |
| c. \(2 \times -3\) means to combine 2 sets of 3 reds: RRR + RRR = RRRRRR = -6. Therefore \(2 \times -3 = -6\) |
|
d. \(-2 \times 3\) means to remove 2 sets of 3 greens from a collection representing zero. (1) Let zero be represented by 6 reds and 15 greens: R R R R R R G G G G G G (2) Remove 2 sets of 3 greens from the above collection, which leaves RRRRRR, which represents -6. Therefore, \(-2 \times 3 = -6\). |
| e. \(3 \times 2\) means to combine 3 sets of 2 greens: GG + GG + GG = GGGGGG = 6. Therefore \(3 \times 2 = 6\) |
| f. \(0 \times -4\) means to combine 0 sets of 4 reds = 0 |
|
g. \(-4 \times 0\) means to remove 4 sets of 0 counters from a collection representing zero. (1) Choose any representation of zero. One possibility is to let zero be represented by 6 reds and 6 greens. R R R R R R G G G G G G (2) Remove 0 sets of 0 counters from the above collection, which leaves the original collection, which represents 0. Therefore, \(-4 \times 0 = 0\). |
8.
\(-3 \times 6\): Remove 3 sets of 6 greens from zero; 5G and 23R; -18
\(-3 \times 6\): Remove 3 sets of 6 greens from zero; 18R; -18
\(-4 \times 4\): Remove 4 sets of 4 greens from zero; 2G and 18R; -16
\(-4 \times -4\): Remove 4 sets of 4 reds from zero; 18G and 2R; 16
\(-5 \times 2\): Remove 5 sets of 2 greens from zero; 4G and 14R; -10
\(-2 \times 5\): Remove 2 sets of 5 greens from zero; 3G and 13R; -10
\(-5 \times -2\): Remove 5 sets of 2 reds from zero; 11G and 1R; 10
\(-2 \times -5\): Remove 2 sets of 5 reds from zero; answers will vary; 10
\(-3 \times 3\): Remove 3 sets of 3 greens from zero; 1G and 10R; -9
\(-3 \times -3\): Remove 3 sets of 3 reds from zero; 12G and 3R; 9
\(-7 \times 2\): Remove 7 sets of 2 greens from zero; answers will vary; -14
\(-2 \times 8\): Remove 2 sets of 8 greens from zero; 2G and 18R; -16
\(-2 \times -8\): Remove 2 sets of 8 reds from zero; 18G and 2R; 16
9.
| a. positive | b. negative | c. zero | d. positive |
10.
| a. Closed |
| b. Closed |
| c. Not Closed: one counterexample is: \(-2 \times -8 = 16\) |
| d. Not Closed: one counterexample is: \(-1 \times -1 = 1\) |
| e. Closed |
| f. Closed |
11.
| a. true |
| b. true |
| c. true |
| d. false; 2 < 3; Multiply both sides by 5: \(2 \times 5 > 3 \times 5\) is false. |
| e. true |
| f. false: 2 < 3; Multiply both sides by -5: \(2 \times -5 > 3 \times -5\) is false. |
12.
| a. If a > b and b > c, then a > c |
| b. If a > b, then a + c > b + c |
| c. If a > b, then ap > bp |
| d. If a > b, then an < bn |
Homework Solutions
2.
| a. 16 | c. 2 | e. 8 |
3. a. 4 and -4
4.
| a. +7 | c. -9 |
5.
| a. 2 – (-5) | c. 3 – 12 |
6. -8 + 5 + (-3) = -6, since the terminal point of the last vector landed on -6.

8.
|
a. 5 – 11 = -6 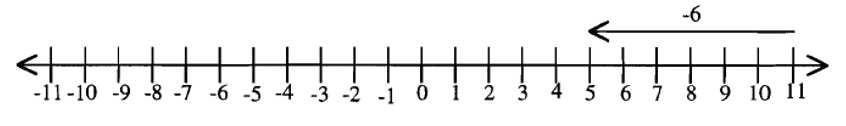 |
|
c. 5 – (-11)= 16 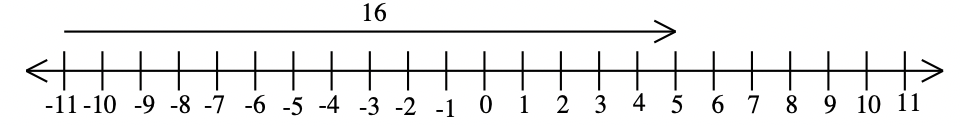 |
9.
a. (1) -4 + (-3) means to combine 4 reds and 3 reds: RRRR + RRR = RRRRRRR, which represents -7
(2) Therefore, -4 + -3 = -7
10.
a. (1) 6 – 8 means remove 8 greens from a collection of counters representing +6.
(2) Represent +6 with 6 greens: GGGGGG
(3) Add 2 red-green pairs (zero) to the collection:
G G G G G G G G
R R
(4) Remove 8 greens, leaving RR, which represents -2.
(5) Therefore, 6 – 8 = -2
11.
| a. Closed |
| b. Not closed; a counterexample is 3 – 10 = -7 |
| c. Closed |
12.
a. \(-5 \times 3\) means to remove 5 sets of 3 greens from a collection representing zero.
(1) Let zero be represented by 15 reds and 15 greens:
R R R R R R R R R R R R R R R
G G G G G G G G G G G G G G G
(2) Remove 5 sets of 3 greens from the above collection, which leaves
RRRRRRRRRRRRRRR, which represents -15. Therefore, \(-5 \times 3 = -15\).
Homework Solutions
2.
| a. 16 | c. 2 | e. 8 |
3. a. 4 and -4
4. a. +7
5.
| a. 2 – (-5) | c. 3 – 12 |
6. -8 + 5 + -3 = -6, since the terminal point of the last vector landed on -6.

8.
|
a. 5 – 11 = -6  |
|
c. 5 – (-11) = 16  |
9.
a. (1) -4 + -3 means to combine 4 reds and 3 reds: RRRR + RRR = RRRRRRR, which represents -7
(2) Therefore, -4 + -3 = -7
10.
a. (1) 6 – 8 means remove 8 greens from a collection of counters representing +6.
(2) Represent +6 with 6 greens: GGGGGG
(3) Add 2 red-green pairs (zero) to the collection:
G G G G G G G G
R R
(4) Remove 8 greens, leaving RR, which represents -2.
(5) Therefore, 6 – 8 = -2
11.
| a. Closed |
| b. Not closed; a counterexample is 3 – 10 = -7 |
| c. Closed |
12.
a. \(-5 \times 3\) means to remove 5 sets of 3 greens from a collection representing zero.
(1) Let zero be represented by 15 reds and 15 greens:
R R R R R R R R R R R R R R R
G G G G G G G G G G G G G G G
(2) Remove 5 sets of 3 greens from the above collection, which leaves RRRRRRRRRRRRRRR, which represents -15. Therefore, \(-5 \times 3 = -15\).
Module 7 Division
Exercise Set 1 Solutions
1.
| a. 2 | b. R | c. R, R |
2.
|
a. P, W, P, W 9, 2, 4, 1, 9, 4, 2, 1  |
|
b. L, R, L, R, 11, 3, 3, 2, 11, 3, 3, 2 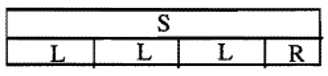 |
|
c. R, blank (or 0) , R, blank (or 0), 8, 4, 2, blank (or 0), 8, 2, 4, blank (or 0)  |
|
d. W, L, W, L, 7, 4, 1, 3, 7, 1, 4, 3  |
|
e. R, blank (or 0), R, blank (or 0), 6, 3, 2, blank (or 0), 6, 2, 3, blank (or 0)  |
3. 2 equal piles of 18 units each

4.
| a. \(210_{\text{four}\) |
| b. Methods will vary. |
| c. \(102_{\text{four}}\) |
| d. \(210_{\text{four}}, 102_{\text{four}}\) |
5.
| a. \(1100_{\text{three}}\) |
| b. Methods will vary. |
| c. \(200_{\text{three}}\) |
| d. \(1100_{\text{three}}, 200_{\text{three}}\) |
7.
| a. \(210_{\text{four}}\) |
| b. Methods will vary. |
| c. \(30_{\text{four}}\) |
| d. \(210_{\text{four}}, 30_{\text{four}}\) |
9.
| a. \(100 \div 4\) |
| b. Partitioning into subsets |
| c. Disburse 100 marbles into 4 equal subsets. |
|
d.  |
| e. \(4 \cdots 25\) |
| f. Count how many marbles were placed in one of the equal subsets. |
| g. 25 |
10.
| a. \(80 \div 8\) |
| b. Repeated Subtraction |
| c. Put 8 ounces in a subset at a time. |
|
d.  |
| e. \(10 \cdots 8\) |
| f. Count how many subsets, each having 8 ounces, were made. |
| g. 10 |
11.
| a. \(144 \div 16\) |
| b. Repeated Subtraction |
| c. Count out 16 pages at a time. |
|
d.  |
| e. \(9 \cdots 16\) |
| f. Count how many short stories, each having 16 pages, were made. |
| g. 9 |
12.
| a. \(500 \div 4\) |
| b. Partitioning into subsets |
| c. Disburse $500 into 4 equal subsets. |
|
d.  |
| e. \(4 \cdots 125\) |
| f. Count how much money was placed in one of the equal subsets. |
| g. $125 |
13.
| a. \(8 \div 1\frac{1}{3}\) |
| b. Repeated Subtraction |
| c. Put 1\(\frac{1}{3}\) cups into a subset at a time. |
|
d.  |
| e. \(6 \cdots 1\frac{1}{3}\) |
| f. Count how many subsets were formed. |
| g. 6 |
14.
| a. \(65 \div 13\) |
| b. Partitioning into subsets |
| c. Disburse 65 baseballs into 13 equal subsets. |
|
d.  |
| e. \(13 \cdots 5\) |
| f. Count how baseballs were placed in one of the equal subsets. |
| g. 5 |
15.
|
d.  |
| e. \(12 \cdots 4\) |
|
g.  |
| h. \(4 \cdots 12\) |
16.
|
d.  |
| e. \(4 \cdots 50\) |
| g. Put 4 into a subset at a time. |
| h. \(50 \cdots 4\) |
17.
| d. Draw 50 subsets, then disburse 150 amongst the 50 subsets. |
| e. \(50 \cdots 3\) |
|
g.  |
| h. \(3 \cdots 50\) |
18.
| d. Draw 35 subsets, then disburse 140 amongst the 35 subsets. |
| e. \(35 \cdots 4\) |
|
g.  |
| h. \(4 \cdots 35\) |
19.
|
d.  |
| e. \(5 \cdots 19\) |
| g. Put 5 into a subset at a time. |
| h. \(19 \cdots 5\) |
19.
|
d.  |
| e. \(5 \cdots 19\) |
| g. Put 5 into a subset at a time. |
| h. \(19 \cdots 5\) |
19.
|
d.  |
| e. \(5 \cdots 19\) |
| g. Put 5 into a subset at a time. |
| h. \(19 \cdots 5\) |
22.
| a. \(56 \div 8\) |
| b. \(40 \div 5\) |
23.
| a. \(18 \div 9\) |
| b. \(10 \div 2\) |
24. a represents how many subsets and b represents how many are in each subset.
25.
| a. Since 32 = 8 \(\cdots\) 4, then \(32 \div 8\) = 4 |
| b. Since 56 = 8 \(\cdots\) 7, then 56 \(\div\) 8 = 7 |
| c. Since 32 = 2 \(\cdots\) 16, then 32 \(\div\) 2 = 16 |
| d. Since 0 = 13 \(\cdots\) 0, then 0 \(\div\) 13 = 0 |
| e. Since 12 = 1 \(\cdots\) 12, then 12 \(\div\) 1 = 12 |
| f. Since X = 1 \(\cdots\) X, then X \(\div\) 1 = X |
| g. Since 0 = Y \(\cdots\) 0, then 0 \(\div\) Y = 0 |
26.
| c. Since 48 = 6 \(\cdots\) 8, then 48 \(\div\) 6 = 8 |
| d. Since there is no whole number solution to make the equation 35= 4 \(\cdots\) __ true, 35 \(\div\) 4 is not defined under whole numbers. |
| e. Since 48 = 1 \(\cdots\) 48, then 48 \(\div\) 1 = 48 |
| f. Since there is no whole number solution to make the equation 55 = 7 \(\cdots\) __ true, 55 \(\div\) 7 is not defined under whole numbers. |
| g. Since 0 = 8 \(\cdots\) 0, then 0 \(\div\) 8 = 0 |
| e. 203 r. 314 |
| f. 248 r. 14 |
27.
| a. There is no number that will make the equation, 6 = 0 \(\cdots\) ____ true, since any number put in the blank will make the right hand side of the equation zero, which can never equal the left-hand side of the equation, which is 6. Therefore, \(6 \div 0\) is not defined. |
| b. There is no number that will make the equation, 18 = 0 \(\cdots\)____ true, since any number put in the blank will make the right hand side of the equation zero, which can never equal the left-hand side of the equation, which is 18. Therefore, \(18 \div 0\) is not defined. |
| c. There is no number that will make the equation, M = 0 \(\cdots\)____ true, since any number put in the blank will make the right handside of the equation zero, which can never equal the left-hand side of the equation, which is M (since it is assumed that M is not equal to zero). Therefore, \(M \div 0\) is not defined. |
Exercise Set 2 Solutions
1.
| a. 6 r. 43 |
| b. 7 r. 20 |
| c. 8 r. 8 |
| d. 3 r. 194 |
| e. 5 r. 55 |
| f. 5 r. 165 |
| g. 9 r. 239 |
2.
| a. 45 r. 15 |
| b. 12 r. 27 |
| c. 32 r. 34 |
| d. 81 r. 29 |
3.
| a. 45 r. 15 |
| b. 12 r. 27 |
| c. 32 r. 34 |
| d. 81 r. 29 |
| e. 203 r. 314 |
| f. 248 r. 14 |
Exercise Set 3 Solutions
1.
| a. F F L L U U |
|
b. i. LUU, LUU, LUU, LUU, LUU ii. U |
| c. UUUUU |
| d. quotient: LUU, remainder: U |
| e. \(12_{\text{three}}r. 1_{\text{three}}\) |
| f. \(12_{\text{three}} \cdots 12_{\text{three}} + 1_{\text{three}} = 221_{\text{three}} + 1_{\text{three}} = 222_{\text{three}}\) |
2.
| a. \(13_{\text{five}}r. 3_{\text{five}}\) |
| b. \(32_{\text{six}}r. 21_{\text{six}}\) |
| c. \(11_{\text{four}}r. 10_{\text{four}}\) |
| d. \(110_{\text{two}}r. 1_{\text{two}}\) |
3.
| a. \(23_{\text{seven}}r. 3_{\text{seven}}\) |
| b. \(102_{\text{three}}\) |
Exercise Set 3 Solutions
1.
| a. F F L L U U |
|
b. i. LUU, LUU, LUU, LUU, LUU ii. U |
| c. UUUUU |
| d. quotient: LUU, remainder: U |
| e. \(12_{\text{three}}r. 1_{\text{three}}\) |
| f. \(12_{\text{three}} \cdots 12_{\text{three}} + 1_{\text{three}} = 221_{\text{three}} + 1_{\text{three }}= 222_{\text{three}}\) |
2.
| a. \(13_{\text{five}}r. 3_{\text{five}}\) |
| b. \(32_{\text{six}}r. 21_{\text{six}}\) |
| c. \(11_{\text{four}} r. 10_{\text{four}}\) |
| d. \(110_{\text{two}} r. 1_{\text{two}}\) |
3.
| a. \(23_{\text{seven}}r. 3_{\text{seven}}\) |
| b. \(102_{\text{three}}\) |
4. \(12_{\text{three}}r. 1_{\text{three}}\)
5. \(13_{\text{five}}r. 3_{\text{five}}\)
6. \(11_{\text{four}}r. 10_{\text{four}}\)
7. \(32_{\text{six}}r. 21_{\text{six}}\)
8. \(110_{\text{two}}r. 1_{\text{two}}\)
9. \(23_{\text{seven}}r. 3_{\text{seven}}\)
10. \(102_{\text{three}}\)
11. \(31_{\text{five}}r. 2_{\text{five}}\)
12. \(111_{\text{two}}r. 101_{\text{two}}\)
13. \(61_{\text{eight}}r. 6_{\text{eight}}\)
14. \(T2_{\text{thirteen }}r. E_{\text{thirteen}}\)
15. \(23_{\text{twelve}}r. 1E_{\text{twelve}}\)
Homework Solutions
1.
| a. \(72 \div 4\) |
| b. Repeated subtraction |
| c. Put 4 lollipops in a bag at a time by repeatedly subtracting 4 from 72 until you run out of lollipops. |
|
d.  |
| e. \(18 \cdots 4\) |
| f. Count how many subsets of 4 you made, how many bags of lollipops there are. |
| g. 18 |
7.
|
a.  |
|
b.  |
| c. Partitioning into subsets is easier, because you only need to make 2 equal subsets as opposed to subtracting 2 at a time. |
11.
| a. the number of subsets |
| b. amount in each subset |
13. \(56_{\text{seven}}r. 22_{\text{seven}}\)
15. \(285_{\text{eleven}}r. 167_{\text{eleven}}\)
17. \(2111_{\text{three}}r. 210_{\text{three}}\)
18.
| a. Not closed; \(-1 \div -1 = 1\) |
| c. Not closed; \(1 \div 0\) is undefined |
19. No; \(10 \div 2 = 5\), but \(2 \div 10 = 1/2\). Therefore, \(10 \div 2 \nleq 2 \div 10\). Use a different counterexample in your answers.
Module 8 Number Theory
Exercise Set 1 Solutions
1.
| a. 7 | b. 3 |
| c. 8 | d. 1 |
| e. 2 | f. 8 |
| g. 2 | h. 8 |
| i. 0 | j. 2 |
| k. 4 | l. 0 |
| m. 7 | n. 8 |
2. same answers as for exercise 1
3. Yes.
4.
|
a. Ck: 6 + 7 = 13 → 4 \(4 \nleq 2\); mistake |
|
b. Ck: 5 + 1 = 6 6 = 6; correct |
|
c. Ck: 2 + 3 = 5 \(5 \nleq 4\); mistake |
|
d. Ck: 8 + 2 + 5 = 15 → 6 6 = 6; correct |
|
e. Ck: 5 + 2 + 2 = 9 → 0 \(0 \nleq 3\); mistake |
|
f. Ck: 1 + 7 + 0 = 8 8 = 8; correct |
5.
|
a. \(2 \cdots 8 = 16 → 7\) 7 = 7; correct |
|
b. \(2 \cdots 0 = 0\) \(0 \nleq 8\); mistake |
|
c. \(5 \cdots 1 = 5\) 5 = 5; correct |
|
d. \(2 ·\cdots 7 = 14 → 5\) \(5 \nleq 4\); mistake |
|
e. \(0 \cdots 1 = 0\) 0 = 0; correct |
|
f. 3 · 7 = 21 → 3 \(3 \nleq 4\); mistake |
|
g. \(2 \cdots 7 = 14 → 5\) 5 = 5; correct |
|
h. \(5 \cdots 2 = 10 → 1\) \(1 \nleq 0\); mistake |
|
i. \(2 \cdots 6 = 12 → 3\) 3 = 3; correct |
6. Do the problems, then check your answers using digital roots.
7.
|
a. 0 + 5 = 5 5 = 5; correct |
|
b. 8 + 0 = 8 8 = 8; correct |
|
c. 5 + 3 = 8 \(8 \nleq 6\); mistake |
|
d. 8 + 6 = 14 → 5 \(5 \nleq 4\); mistake |
|
e. 5 + 4 = 9 → 0 0 = 0; correct |
|
f. 1 + 4 = 5 5 = 5; correct |
8. Do the problems, then check your answers using digital roots.
9.
|
a. \(1 \cdots 4 = 4; 4 + 7 = 11 → 2\) 2 = 2; correct |
|
b. \(6 \cdots 0 = 0; 0 + 0 = 0\) 0 = 0; correct |
|
c. \(8 \cdots 8 = 64 → 10 → 1; 1 + 1 = 2\) \(2 \nleq 4\); mistake |
|
d. \(6 \cdots 3 = 18 → 0; 0 + 5 = 5\) 5 = 5; correct |
10. Do the problem, then check your answer using digital roots.
11.
| a. This is a division problem. The answer is 5. |
| b. This is a false statement since 35 is not a factor of 7. |
| c. This is a true statement since 7 is a factor of 35; (\(7 \cdots 5 = 35\)) |
| d. This is a division problem. The answer is 5 r. 5. |
| e. This is a false statement since 56 is not a factor of 8. |
| f. This is a false statement since 7 is not a factor of 40. |
| g. This is a true statement since 12 is a factor of 60; (\(12 \cdots 5 = 60\)) |
| h. This is a division problem. The answer is 2 r. 20. |
| i. This is a division problem. The answer is 14. |
| j. This is a false statement since 42 is not a factor of 3. |
| k. This is a true statement since 6 is a factor of 42; (\(6 \cdots 7 = 42\)) |
| l. This is a division problem. The answer is 8. |
| m. This is a division problem. The answer is 50. |
| n. This is a true statement since 4 is a factor of 100; (\(4 \cdots 25 = 100\)) |
| o. This is a false statement since 4 is not a factor of 90. |
| p. This is a false statement since 25 is not a factor of 5. |
13. The proof is written exactly like Example 1 shown above this exercise if a is replaced by x, b is replaced by y, and c is replaced by z.
18. If a is a factor of b, then am = b for some whole number, m. If a is a factor of c, then an = c for some whole number n. Using substitution, bc = (am)(an) = a(amn), which shows a is a factor of bc.
19. The proof is written exactly like the example shown above this exercise if a is replaced by c, b is replaced by a, and c is replaced by b.
20.
| a. 2|9,712 since the last digit is even. |
| b. 5,643 is odd, so it is not divisible by 2. |
| c. 5,690 is not divisible by 4 since 4 is not a factor of 90. |
| d. 63,868 is divisible by 4 since 4 is a factor of 68. |
| e. 854,100 is divisible by 4 since 4 is a factor of 0. |
| f. 8 is a factor of 12,345,248 since 8 is a factor of 248. |
| g. 54,094,422 is not divisible by 8 since 8 is not a factor of 422. |
21.
| a. 5|9,750 since the last is 0. |
| b. 5|5,645 since the last is 5. |
| c. 5,696 is not divisible by 5 since the last digit is not 0 or 5. |
| d. 10|63,860 since the last digit is 0. |
| e. 854,105 is not divisible by 10 since the last digit is not 0. |
22.
| a. 3|9,750 since 3|3, where 3 is the digital root of 9,750. |
| b. 3|5,645 is false since 3 is not a factor of 2, which is the d.r. of 5,645. |
| c. 3|5,696 is false since 3 is not a factor of 8, the d.r. of 5,696. |
| d. 3|63,860 is false since 3 is not a factor of 5, the d.r. of 63,860. |
| e. 3|854,115 since 3|6, where 6 is the d.r. of 854,115. |
23.
| a. 9|9,753 is false since the digital root of 9,753 is 6, not 0. |
| b. 9|5,646 is false since the d.r. of 5,646 is 3, not 0. |
| c. 9|5,697 since the digital root of 5,697 is 0. |
| d. 9|63,576 since the digital root of 63,576 is 0. |
| e. 9|854,103 is false since the d.r. of 854,103 is 3, not 0. |
24.
| a. 6|9,753 is false since 9,753 is not even, therefore not divisible by 2. |
| b. 6|5,645 is false since 5,645 is not even, therefore not divisible by 2. |
| c. 6|5,696 is false since 3 is not a factor of 8, which is the d.r. of 5,696. |
| d. 6|63,876 since it is even and is also divisible by 3, since the d.r. is 3. |
| e. 6|854,103 is false since 854,103 is not even, therefore not divisible by 2. |
25.
| a. 15|9,753 is false since it is not divisible by 5. |
| b. 15|6,645 since both 3 and 5 are factors. |
| c. 15|1,690 is false since 3 is not a factor. |
| d. 15|63,872 is false since 5 is not a factor. |
| e. 15|654,105 since it is divisible by both 3 and 5. |
26. Include justification
| a. true |
| b. false |
| c. true |
| d. true |
27. Include justification
| a. true |
| b. false |
| c. false |
| d. true |
| e. false |
Exercise Set 2 Solutions
1. c. 1, 2, 3, 4, 6, 12
2.
| a. 1, 2 |
| b. 1, 3 |
| c. 1, 2, 4 |
| d. 1, 5 |
| e. 1, 2, 3, 6 |
| g. 1, 2, 4, 8 |
| h. 1, 3, 9 |
| i. 1, 2, 5, 10 |
| j. 1, 11 |
| k. 1, 13 |
| l. 1, 2, 7, 14 |
| m. 1, 3, 5, 15 |
| n. 1, 2, 4, 8, 16 |
3.
| a. 2, 3, 5, 7, 11, 13 |
| b. The only factors are 1 and the number itself. |
| c. 4, 9, 16 |
| d. They are perfect squares. |
4.
| a. \(45 = 3 \cdots 3 \cdots 5\) |
| b. \(65 = 5 \cdots 13\) |
| c. \(200 = 2 \cdots 2 \cdots 2 \cdots 5 \cdots 5\) |
| d. \(91 = 7 \cdots 13\) |
| e. \(76 = 2 \cdots 2 \cdots 19\) |
| f. \(350 = 2 \cdots 5 \cdots 5 \cdots 7\) |
| g. \(189 = 3 \cdots 3 \cdots 3 \cdots 7\) |
| h. \(74 = 2 \cdots 37\) |
| i. \(512 = 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2 \cdots 2\) |
| j. \(147 = 3 \cdots 7 \cdots 7\) |
5. 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
6. 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48
7. 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, 90, 91, 92, 93, 94, 95, 96, 98, 99, 100, 102, 104, 105, 106, 108, 110, 111, 112, 114, 115, 116, 117, 118, 119, 120
8. \(11 \cdots 47\)
9. 22.7
10.
| a. 11; 149 |
| b. 13; 3 · 7 · 13 |
| c. 19; 3 · 127 |
| d. 19; 19 · 23 |
| e. 19; 509 |
| f. 23; 613 |
| g. 23; 787 |
11.
| a. \(2 \cdots 2 \cdots 2 \cdots 5 \cdots 7\) |
| b. 281 |
| c. \(2 \cdots 3 \cdots 47\) |
| d. 283 |
| e. \(2 \cdots 2 \cdots 71\) |
| f. \(5 \cdots 3 \cdots 19\) |
| g. \(2 \cdots 11 \cdots 13\) |
| h. \(7 \cdots 41\) |
| i. \(25 \cdots 3 \cdots 3\) |
| j. \(17 \cdots 17\) |
| k. \(2 \cdots 5 \cdots 29\) |
| l. \(3 \cdots 97\) |
| m. \(2 \cdots 2 \cdots 73\) |
| n. 293 |
| o. \(2 \cdots 3 \cdots 7 \cdots 7\) |
| p. \(5 \cdots 59\) |
12. 281 and 283
13. No; at least one will be a multiple of 3.
14.
| a. 1, 2, 3, 6, 7, 14, 42 |
| b. 1, 2, 5, 7, 10, 14, 35, 70 |
| c. 1, 2, 7, 14 |
| d. 14 |
| e. 14 |
15.
| a. 1, 2, 4, 23, 46, 92 |
| b. 1, 5, 23, 115 |
| c. 1, 23 |
| d. 23 |
| e. 23 |
16.
| a. 1, 2, 3, 4, 6, 8, 12, 16, 24, 48 |
| b. 1, 2, 3, 6, 9, 18, 27, 54 |
| c. 1, 3, 7, 9, 21, 63 |
| d. 1, 3 |
| e. 3 |
| f. 3 |
17.
| a. 14 | b. 23 | c. 3 |
| d. 34 | e. 25 | f. 42 |
18. a. \(24 \cdots 3 \cdots 132\)
19.
| a. \(2^{4} \cdots 3^{2} \cdots 7^{6} \cdots 13^{2}\) |
| b. \(3^{4} \cdots 5^{2}\) |
| c. \(a^{4} \cdots c^{3} \cdots d^{3} \cdots e^{2}\) |
| d. \(a^{2} \cdots d^{3}\) |
22. a. 2, 7
23. 1
24.
| a. m | b. 2m | c. m |
| d. 1 | e. m |
25. a - g: 1, 2, 3, 6
h. same factors
26. a - f: 6
27.
| a. 13 | b. 18 | c. 36 |
28.
| a. 38 r. 186 |
| b. 9 r. 33 |
| c. 7 r. 11 |
| d. 8 r. 25 |
29.
| a. 13 | b. 18 | c. 36 |
30. d. 22
31. d. 31
32. d. 1
34. 14|n if 2|n and 7|n.
35.
| a. True since 2|742 and 7|742 |
| b. False –7 is not a factor of 968 |
| c. False –2 is not a factor of 483 |
36. Think about why YOU think it doesn't work. This is a question only you can answer.
37. Think about why YOU think it works. This is a question only you can answer.
38.
| a. 4|n and 3|n |
| b. 9|n and 2|n |
39.
| a. 35|n if 5|n and 7|n |
| b. 28|n if 4|n and 7|n |
| c. 75|n if 3|n and 25|n |
| d. 56|n if 7|n and 8|n |
| e. c|n if 4|n, 27|n, 25|n and 11|n |
| f. d|n if 16|n, 3|n, 5|n and 11|n |
40.
| a - e. 1 |
| f. No; 1 is the smallest factor of every number. |
Exercise Set 3 Solutions
1.
| a. 8, 16, 24, 32, 40, 48, 56, 64, 72, 80 |
| b. 12, 24, 36, 48, 60, 72, 84, 96, 108, 120 |
| c. 24, 48, 72 |
| d. 24 |
| e. no |
2.
| a. 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60 |
| b. 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 66, 72, 78, 84, 90 |
| c. 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150 |
| d. 60 |
| e. 60 |
5.
| a. X, Y |
| b. Y, Z |
| c. X, Y |
7. \(2^{2} \cdots 3^{5} \cdots 5 \cdots 7^{3} \cdots 11^{2} \cdots 1^{3}\)
8. \(2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 11^{2} \cdots 13^{2} \cdots 1^{9}\)
9. \(2^{4} \cdots 3^{6} \cdots 5^{4} \cdots 7^{6} \cdots 11^{2} \cdots 1^{9} \cdots 23^{2}\)
10.
|
a. GCF: \(2^{2} \cdots 3^{2} \cdots 1^{3}\) LCM: \(2^{2} \cdots 3^{5} \cdots 5 \cdots 7^{3} \cdots 1^{3}\) |
|
b. GCF: 2 LCM: \(2^{2} \cdots 3^{4} \cdots 7^{3} \cdots 11^{2} \cdots 13^{2} \cdots 1^{9}\) |
|
c. GCF: \(c^{3} \cdots d\) LCM: \(a^{5} \cdots b^{4} \cdots c^{5} \cdots d^{3} \cdots e^{2}9\). |
|
d. GCF: \(c \cdots d\) LCM: \(a^{6} \cdots b^{4} \cdots c^{4} \cdots d^{3} \cdots e^{7}\) |
11.
| a. 120 |
| b. 1400 |
| c. 1274 |
| d. 840 |
| e. 1870 |
12.
| a. 3 · 2 · 2 · 7 · 3 · 5 = 1260 |
| b. 2·3·3·11·7·5·2·2·2·17 = 942,480 |
| c. 5·2·3·7·2·2·17·3·5 = 214,200 |
| d. 3 · 5 · 2 · 3 · 2 · 5 · 7 = 6,300 |
13. 14,112
14. 2,835
15. 3,705
16. 2 and 20; 4 and 10
17.
| a. 21 | b. 18,018 |
18.
| a. 73 | b. 74,095 |
19.
| a. 37 | b. 395,641 |
20.
| a. 6 | b. 58,344,300 |
25.
| a. 2(4n + 10) is an even number. |
| b. 2(5k + 4) + 1 is an odd number. |
| c. 5x + 2 can be even or odd |
26. Let 2n = one even number, and let 2m = another even number. The sum is: 2n+2m = 2(n+m), which is in the form of an even number. Therefore, the sum of 2 even numbers is even.
27. Let 2n + 1 = one odd number, and let 2m + 1 = another odd number. The sum is: 2n + 1 + 2m + 1 = 2n + 2m + 2 = 2(n + m + 1), which is in the form of an even number. Therefore, the sum of 2 odd numbers is even
28. Let 2n = one even number, and let 2m + 1 = one odd number. The sum is: 2n + 2m + 1 = 2n + 2m + 1 = 2(n + m) + 1, which is in the form of an odd number. Therefore, the sum of an even number and an odd number is odd.
29. Let 2n = one even number, and let 2m = another even number. The product is: 2n · 2m = 4mn = 2(2mn), which is in the form of an even number. Therefore, the product of two even numbers is even.
30. Let 2n + 1 = one odd number, and let 2m + 1 = one odd number. The product is: (2n + 1)(2m + ) = 2nm + 2m + 2n + 1 = 2(nm + m + n) + 1, which is in the form of an odd number. Therefore, the product of two odd numbers is odd.
31. Let 2n = one even number, and let 2m + 1 = one odd number. The product is: 2n(2m + 1) = 4nm + 2n = 2(2nm + n), which is in the form of an even number. Therefore, the product of an even number and an odd number is even.
32. 3240
33. 3240
34. 31,375
35.
| a. 3,77 |
| b.148,181 |
| c.195,650 |
36.
| a. 3,775 |
| b. 148,181 |
| c. 195,650 |
| d.[n –(k –1)]\((n + k) \div 2\) or (n –k + 1)\((n + k) \div 2\) |
37. multiples of 7
38. 1 + 2 + 3 + . . . + 99 + 100
39.
| a. 5,050 |
| b. 5,050 |
| c. 35,350 |
40.
| a. 63,000 |
| b. 41,151 |
| c. 226,500 |
41. multiples of 4
42. 28 + 29 + 30 + . . . + 131 + 132
43. 33,600
44.
| a. 54,450 |
| b. 96,019 |
45. 6
46. 4, 8, 14
47. 4, 6
48. 4
49. 8
50. 3, 7
51. 7
52. 68, 178, 288, 398, 508, 618, 728, 838, 948
53. 5
54. 5
55. 5 or 26
56. mult. of 7
57. 9 or 23
58. 3, 5, or 9
59. 9
60. Yes; explanation not provided here
Homework Solutions
1. GCF:14; LCM: 6,300
3. a. GCF: 47; LCM: 49,350
4. a. Since the number is even, we only need to make the resulting number divisible by 3. The digital root so far is 8. So, decide which single digits could be added to 8 to get a number that is still divisible by 3. Adding 1, 4 or 7 to 8 will work. So the possibilities are 4, 7 or 8.
5. The examples and counterexamples are not provided by these solutions. Make sure you provide them!
| a. false |
| b. true |
6.
| a. \(7 \cdots 53\) |
| d. \(7 \cdots 41\) |
7.
| a. m |
| b. m |
| c. m |
| d. 1 |
9.
| a. 49,770 |
| b. 35,800 |
10.
| a. 39 |
| b. 80 |
11.
| a. 1, 2, 3; 6; perfect |
| b. 1; 1; deficient |
| c. 1, 2, 4; 7; deficient |
13. Examples and counterexamples are not provided here. Make sure you provide them.
| a. False |
| b. True |
| c. False |
| d. True |
15. a. 84
Module 9 Rational Numbers
Warm Up Solutions
1. R
2. Y
3. P
4. D
5. O
6. D
7. H
8. B
9. D
10. O
11. Y
12. B
13. B
14. L
Exercise Set 1 Solutions
1. \(\frac{1}{12} < \frac{1}{10} < \frac{1}{9} < \frac{1}{8} < \frac{1}{6} < \frac{1}{5} < \frac{1}{4} < \frac{1}{3} < \frac{1}{2}\)
2.
| a. \(\frac{1}{90}\) | b. \(\frac{1}{32}\) |
3. \(\frac{5}{12} < \frac{5}{10} < \frac{5}{9} < \frac{5}{8} < \frac{5}{6}\)
4.
| a. \(\frac{15}{37}\) | b. \(\frac{89}{100}\) |
5. \(\frac{4}{12} < \frac{4}{11} < \frac{4}{10} < \frac{4}{9} < \frac{4}{8} < \frac{4}{7} < \frac{4}{6} < \frac{4}{5}\)
6. If you are comparing two fractions that have the same numerator, the one with the smaller denominator has the larger value.
7, 8. \(\frac{1}{2} < \frac{2}{3} < \frac{3}{4} < \frac{4}{5} < \frac{5}{6} < \frac{7}{8} < \frac{8}{9} < \frac{9}{10} < \frac{11}{12}\)
9.
| a. \(\frac{94}{95}\) | b. \(\frac{89}{100}\) |
10. \(\frac{13}{14} < \frac{25}{26} < \frac{34}{35} <\frac{45}{46} < \frac{51}{52} < \frac{71}{72} < \frac{99}{100}\)
11. If you are comparing two fractions where in each fraction the numerator is one less than the denominator, the fraction with the bigger numerator and denominator has the larger value.
12. Answers will vary. Try drawing a pie for each fraction, shading in 2 of 3 equal parts for 2/3 and 4 of 5 equal parts for 4/5. Which pie is more shaded?
13. Answers will vary
14. \(\frac{2}{4}\) and \(\frac{3}{6}\) and \(\frac{4}{8}\) and \(\frac{5}{10}\) and \(\frac{6}{12}\)
15. \(\frac{4}{6}\) and \(\frac{6}{9}\) and \(\frac{8}{12}\)
16 - 17: There are many possibilities using multiple strips.
18. Multiply the numerator and denominator by the same number to get an equivalent fraction.
19 - 27. Only the final answers are shown below. Make your own models for exercises 22 - 28 by following the examples making sure you show all the steps, define units, rows, columns, etc.
19. \(\frac{3}{4} < \frac{4}{5}\)
20. \(\frac{13}{20}\)
21. \(\frac{5}{24}\)
22.
| a. \(\frac{8}{15}\) | b. \(\frac{15}{24}\) |
23.
| a. \(\frac{2}{3} \cdots \frac{5}{6} = \frac{10}{18}\) | b. \(\frac{1}{2} \cdots \frac{7}{8} = \frac{7}{16}\) |
24.
| a. \(\frac{4}{5} \cdots \frac{3}{5} = \frac{12}{25}\) | b. \(\frac{1}{7} \cdots \frac{3}{4} = \frac{3}{28}\) |
25. Answers may vary. One possibility: Let 1 = H; \(\frac{3}{4}\) of H = B; \(\frac{1}{3}\) of B = L; \(\frac{L}{H} = \frac{3}{12}\)
26.
| a. H; B; L; L/H; 3/12 |
| b. N; R; W; W/N; 1/8 |
| c. N; R; L; L/N; 3/8 |
| d. D; L; R; R/D; 2/6 |
27 - 30. Make your own models. One possibility for each using the C-strip model is given, but there are other choices.
27. Let 1 unit = O, then 1/10 = W and 1/5 = R. There are 2 W in R, so the answer is 2.
28. Let 1 unit = B, then 1/9 = W and 1/3 = L. There are 3 W in L, so the answer is 3.
29. Let 1 unit = H, then 1/6 = R and 2/3 = N. There are 4 R in N, so the answer is 4.
30. Let 1 unit = P, then 1/4 = W and 3 = H. There are 12 W in H, so the answer is 12.
31.
| a. equivalent | b. equivalent | c. not equivalent |
32. There are infinitely many possibilities - you can use the multiple strips to find some.
33. same as #31
34.
| a. \(\frac{14}{25}\) | b. \(\frac{13}{17}\) | c. \(\frac{18}{35}\) | d. \(\frac{15}{22}\) |
35. same as #31
36.
| a. \(\frac{4}{5} > \frac{5}{8}\) | b. \(\frac{12}{35} < \frac{11}{18}\) | c. \(\frac{13}{15} > \frac{14}{17}\) |
37. \(89 \cdots 95 < 90 \cdots 94\) since 8455 < 8460. Cross products check.
38. It checks, show work
39.
| a. -4/70 | b. 71/72 |
40. Answers may vary. Some possibilities: 21/50, 22/50, 23/50, . . . , 29/50
41,42. 1/2
43. Some possibilities: 51/150, 52/150, 53/150, . . . , 59/150
44. Some possibilities: 21/60, 22/60, 23/60, . . . , 29/60
45. 241/300, 242/300, 243/300, . . . , 249/300
46. 83/112
47. 75/112
48. Draw 12 circles. 11 of the circles add up to 66, so put 6 in each circle. Answer: 6 students.
49. Draw 7 circles, Since 3 circles add up to 36, put 12 in each circle. The other 4 circles represent students not buying lunch. Answer: 48 students
50. Draw 8 circles. Since all 8 circles add up to 120, put 15 in each circle. 5 of the circles represent the females, the other three represent the males. Answer: 75 females and 45 males.
Exercise Set 2 Solutions
1.
| a. four tenths; \(\frac{4}{10} = \frac{2}{5}\) |
| b. twenty-six hundredths; \(\frac{26}{100} = \frac{13}{50}\) |
| c. three and eight hundredths; \(3\frac{8}{100} = 3\frac{2}{25}\); \(\frac{388}{100} = \frac{77}{25}\) |
| d. nine and eighty-five hundredths; \(9\frac{85}{100} = 9\frac{17}{20}\); \(\frac{985}{100} = \frac{197}{20}\) |
| e. seventeen and three hundred five thousandths; \(17\frac{305}{1000}= 17\frac{61}{200}\); \(\frac{17305}{1000} = \frac{3461}{200}\) |
2.
| a. 0.14 | b. 008 |
| c. 4\(\frac{35}{100} = 4.35\) | d. 563\(\frac{8}{10} = 563.8\) |
| e. 3\(\frac{5}{100} = 3.05\) |
3.
| a. 0.028 | b. 0.32 |
| c. 0.075 | d. 0.66 |
4.
| a. 1.9; 1.90000 |
| b. 4.0340 |
5.
| a. 3.5 > .9 |
| b. 35.06 = 3.0600 |
| c. 0.089 < 0.0908 |
6.
| a. 3.51 > 3.488 |
| b. 35.061 < 35.35 |
| c. 0.8933 < 0.0894 |
7.
| a. \(2 \cdots 5\) | b. \(2 \cdots 5 \cdots 2 \cdots 5\) |
| c. \(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) | d. \(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) |
| e. \(2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5 \cdots 2 \cdots 5\) |
8. 2 and 5
9. 3
10. 2
11. Well, what do you think?
12.
| a. 0.0875 | b. 0.875 |
13. Write a response in your own words.
14.
| a. \(\frac{3}{4} = \frac{3}{2 \cdots 2} \cdots \frac{5 \cdots 5}{5 \cdots 5} = \frac{75}{100} = 0.75\) |
| b. \(\frac{9}{20} = \frac{3 \cdots 3}{2 \cdots 2 \cdots 5} \cdots \frac{5}{5} = \frac{45}{100} = 0.45\) |
| c. \(\frac{9}{15} = \frac{3 \cdots 3}{3 \cdots 5} = \frac{3}{5} \cdots \frac{2}{2} = \frac{6}{10} = 0.6\) |
| d. \(\frac{18}{25} = \frac{2 \cdots 3 \cdots 3}{5 \cdots 5} \cdots \frac{2 \cdots 2}{2 \cdots 2} = \frac{72}{100} = 0.72}\) |
| e. \(\frac{5}{14} = \frac{5}{2 \cdots 7}\) This can't be written as a terminating decimal because the reduced factor has a prime factor of 7 (which is other than a 2 or 5) in the denominator. |
15. Do three of your own.
16.
| a. 0, 1, 2, 3, 4, 5 |
| b. 0, 1, 2, 3, 4, 5, 6 |
| c. 0, 1, 2, 3, 4, 5, 6, 7, 8 |
| d. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 |
| e. 0, 1, 2 |
17. Do three of your own.
18. a, b, d
19.
| a. There are 33 (including 0 as a remainder). A maximum of 32 digits could be in a sequence without repeating. |
| b. If you do the long division, you get .939393... |
| c. 2 |
| d. 13 and 31 |
20.
| a. 0.\(\bar{5}\) or 0.555... |
| b. 0.\(\bar{714285}\) or 0.714285714285... |
| c. 0.1\(\bar{6}\) or 0.1666... |
| d. 0.\(\bar{6}\) or 0.666.. |
| e. 0.\(\bar{63}\) or 0.636363... |
| f. 0.41\(\bar{6}\) or 0.41666.. |
| g. 0.5\(\bar{3}\) or 0.5333... |
| h. 0.3\(\bar{5}\) or 0.3555... |
| i. 0.0\(\bar{75}\) or 0.0757575... |
21. x - 1
22.
10x = 7.272727...;
100x = 72.727272...;
1000x = 727.272727...
23.
| a. 99x |
| b. 72 |
| c. 99x = 72; x = \(\frac{72}{99}\) |
| d. x = \(\frac{8}{11}\) |
24.
| a. \(\frac{4}{10} =\frac{2}{5}\) | b. \(\bar{4} = \frac{4}{9}\) |
| c. \(\frac{6}{100} = \frac{3}{50}\) | d. \(\bar{0.06} = \frac{6}{99} = \frac{2}{33}\) |
| e. \(\frac{9}{10}\) | f. \(\bar{0.9} = \frac{9}{9} = 1\) Surprise! |
| g. \(\frac{45}{100} = \frac{9}{20}\) | h. 0.\(\bar{45} = \frac{45}{99} = \frac{5}{11}\) |
| i. \(\frac{84}{1000} = \frac{21}{250}\) | j. 0.\(\bar{084} = \frac{84}{999} = \frac{28}{333}\) |
25.
| a. \(\frac{2.8}{99} = \frac{28}{99 \cdots 10} = \frac{14}{495}\) |
| b. \(\frac{2.6}{9} = \frac{26}{9 \cdots 10} = \frac{13}{45}\) |
| c. \(\frac{0.06}{9} = \frac{6}{9 \cdots 100} = \frac{1}{150}\) |
| d. \(\frac{101}{999}\) |
| e. \(\frac{3.6}{9} = \frac{36}{9 \cdots 10} = \frac{2}{5}\) |
26. Be creative!
27. No, since 9 is a perfect square. So, \(\sqrt{9} = 3\)
28-30. Be creative!
31.
| a. rational (repeating decimal). |
| b. irrational (it has a pattern, but does not repeat!) |
| c. rational |
| d. irrational (since 80 is not a perfect square) |
| e. rational (since 100 is a perfect square; so \(\sqrt{100} = 10\) |
| f. irrational |
Homework Solutions
1.
| a. K | c. D | e. D | g. H |
2.
| a. H | c. P | e. R |
3. a. L
7. \(\frac{1}{3} < \frac{3}{8}\)
8. \(\frac{17}{24}\)
9. \(\frac{7}{20}\)
10. a. \(\frac{3}{20}\)
11. a. \(\frac{5}{6} \cdots \frac{2}{3} = \frac{10}{18}\)
12. a. \(\frac{2}{3} \cdots \frac{3}{8} = \frac{6}{24}\)
13. a. B; D; R; R/B; 2/9
14. a. 15
16. a. \(\frac{18}{35}\)
18. Some possibilities: 31/80, 32/80, 33/80, . . . , 49/80
20. a. Draw 10 circles. Since 7 of the circles add up to 21, put 3 in each circle. All 10 circles add up to 30, so there are 30 students.
21.
| a. seven tenths |
| b. three and twenty-eight hundredths |
22.
| a. \(\frac{3}{10} \cdots \frac{8}{10} = \frac{14}{100} = 0.14\) |
| b. \(\frac{122}{100} \cdots \frac{23}{10} = \frac{2086}{1000} = 2.806\) |
23.
| a. \(\frac{11}{16} = \frac{11}{2 \cdots 2 \cdots 2 \cdots 2} \cdots \frac{5 \cdots 5 \cdots 5 \cdots 5}{5 \cdots 5 \cdots 5 \cdots 5} = \frac{6875}{10000} = 0.6875\) |
| c. \(\frac{1}{12} = \frac{1}{2 \cdots 2 \cdots 3}\) |
This can't be written as a terminating decimal because the reduced factor has a prime factor of 3 (which is other than a 2 or 5. in the denominator).
24.
| a. \(\frac{7}{9}\) | c. \(\frac{235}{999}\) |

