18.4: Solving Percentage Problems

Last updated
Save as PDF

Page ID: 39948

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's solve more percentage problems.

Exercise $\PageIndex{1}$: Number Talk: Multiplication with Decimals

Find the products mentally.

$6\cdot (0.8)\cdot 2$

$(4.5)\cdot (0.6)\cdot 4$

Exercise $\PageIndex{2}$: Coupons

Han and Clare go shopping, and they each have a coupon. Answer each question and show your reasoning.

Han buys an item with a normal price of $15, and uses a 10% off coupon. How much does he save by using the coupon?

Figure $\PageIndex{1}$: Coupons 5, by Hobbies on a Budget. CC BY 2.0. Flickr. Source.

Clare buys an item with a normal price of $24, but saves $6 by using a coupon. For what percentage off is this coupon?

Are you ready for more?

Clare paid full price for an item. Han bought the same item for 80% of the full price. Clare said, “I can’t believe I paid 125% of what you paid, Han!” Is what she said true? Explain.

Exercise $\PageIndex{3}$: Info Gap: Music Devices

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the problem card:

Silently read your card and think about what information you need to be able to answer the question.
Ask your partner for the specific information that you need.
Explain how you are using the information to solve the problem.
Continue to ask questions until you have enough information to solve the problem.
Share the problem card and solve the problem independently.
Read the data card and discuss your reasoning.

If your teacher gives you the data card:

Silently read your card.
Ask your partner “What specific information do you need?” and wait for them to ask for information.
If your partner asks for information that is not on the card, do not do the calculations for them. Tell them you don’t have that information.
Before sharing the information, ask “Why do you need that information?” Listen to your partner’s reasoning and ask clarifying questions.
Read the problem card and solve the problem independently.
Share the data card and discuss your reasoning.

Summary

A pot can hold 36 liters of water. What percentage of the pot is filled when it contains 9 liters of water?

Here are two different ways to solve this problem:

Using a double number line:

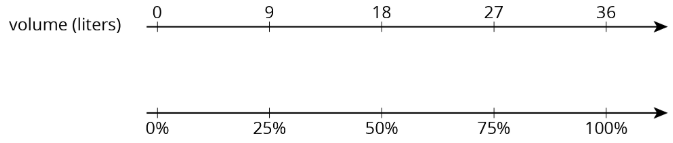
We can divide the distance between 0 and 36 into four equal intervals, so 9 is $\frac{1}{4}$ of 36, or 9 is 25% of 36.

Using a table:

Figure $\PageIndex{3}$: A table with two columns. First column, volume in liters, 36, 9. Second column, percentage, 100, 25. Outside the table, an arrow on each side labeled times fraction one over four points from the first data row to the second data row.

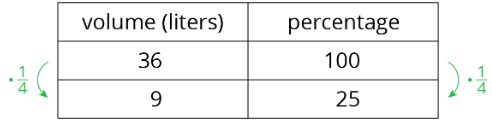
Glossary Entries

Definition: Percent

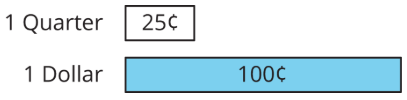
The word percent means “for each 100.” The symbol for percent is %.

For example, a quarter is worth 25 cents, and a dollar is worth 100 cents. We can say that a quarter is worth 25% of a dollar.

Figure $\PageIndex{5}$: A diagram of two bars with different lengths. The top bar is labeled 1 Quarter and 25 cents is labeled inside the bar. The bottom bar is labeled 1 Dollar. It is 4 times longer than the top bar and 100 cents is labeled inside the bar.

Definition: Percentage

A percentage is a rate per 100.

For example, a fish tank can hold 36 liters. Right now there is 27 liters of water in the tank. The percentage of the tank that is full is 75%.

Practice

Exercise $\PageIndex{4}$

For each problem, explain or show your reasoning.

160 is what percentage of 40?
40 is 160% of what number?
What number is 40% of 160?

Exercise $\PageIndex{5}$

A store is having a 20%-off sale on all merchandise. If Mai buys one item and saves $13, what was the original price of her purchase? Explain or show your reasoning.

Exercise $\PageIndex{6}$

The original price of a scarf was $16. During a store-closing sale, a shopper saved $12 on the scarf. What percentage discount did she receive? Explain or show your reasoning.

Exercise $\PageIndex{7}$

Select all the expressions whose value is larger than 100.

120% of 100
50% of 150
150% of 50
20% of 800
200% of 30
500% of 400
1% of 1,000

Exercise $\PageIndex{8}$

An ant travels at a constant rate of 30 cm every 2 minutes.

At what pace does the ant travel per centimeter?
At what speed does the ant travel per minute?

(From Unit 3.3.4)

Exercise $\PageIndex{9}$

Is $3\frac{1}{2}$ cups more or less than 1 liter? Explain or show your reasoning. (Note: 1 cup $\approx$ 236.6 milliliters)

(From Unit 3.2.3)

Exercise $\PageIndex{10}$

Name a unit of measurement that is about the same size as each object.

The distance of a doorknob from the floor is about 1 _____________.
The thickness of a fingernail is about 1 _____________.
The volume of a drop of honey is about 1 _____________.
The weight or mass of a pineapple is about 1 _____________.
The thickness of a picture book is about 1 _____________.
The weight or mass of a buffalo is about 1 _____________.
The volume of a flower vase is about 1 _____________.
The weight or mass of 20 staples is about 1 _____________.
The volume of a melon is about 1 _____________.
The length of a piece of printer paper is about 1 _____________.

(From Unit 3.2.1)

Search

Text Color

Text Size

Margin Size

Font Type