18.5: Finding This Percent of That

Last updated
Save as PDF

Page ID: 39947

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's solve percentage problems like a pro.

Exercise $\PageIndex{1}$: Number Talk: Decimals

Find the value of each expression mentally.

$(0.23)\cdot 100$

$50\div 100$

$145\cdot\frac{1}{100}$

$7\div 100$

Exercise $\PageIndex{2}$: Audience Size

A school held several evening activities last month—a music concert, a basketball game, a drama play, and literacy night. The music concert was attended by 250 people. How many people came to each of the other activities?

Attendance at a basketball game was 30% of attendance at the concert.
Attendance at the drama play was 140% of attendance at the concert.
Attendance at literacy night was 44% of attendance at the concert.

Are you ready for more?

50% of the people who attended the drama play also attended the music concert. What percentage of the people who attended the music concert also attended the drama play?

Exercise $\PageIndex{3}$: Everything is On Sale

During a sale, every item in a store is 80% of its regular price.

If the regular price of a T-shirt is $10, what is its sale price?

The regular prices of five items are shown here. Find the sale price of each item.

Table $\PageIndex{1}$
	item 1	item 2	item 3	item 4	item 5
regular price	$$1$	$$4$	$$10$	$$55$	$$120$
sale price

You found 80% of many values. Was there a process you repeated over and over to find the sale prices? If so, describe it.

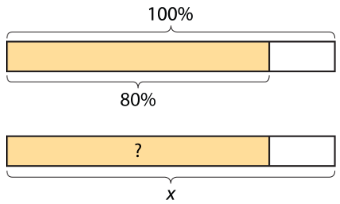
Select all of the expressions that could be used to find 80% of $x$. Be prepared to explain your reasoning.

$\begin{array}{lllllllll}{\frac{8}{100}\cdot x}&{\qquad}&{\frac{8}{10}\cdot x}&{\qquad}&{\frac{8}{5}\cdot x}&{\qquad}&{80\cdot x}&{\qquad}&{(0.8)\cdot x}\\{\frac{80}{100}\cdot x}&{\qquad}&{\frac{4}{10}\cdot x}&{\qquad}&{\frac{4}{5}\cdot x}&{\qquad}&{8\cdot x}&{\qquad}&{(0.08)\cdot x}\end{array}$

Summary

To find 49% of a number, we can multiply the number by $\frac{49}{100}$ or $0.49$.

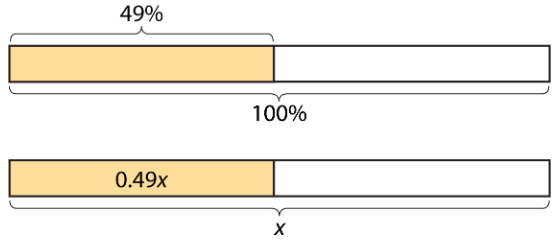
To find 135% of a number, we can multiply the number by $\frac{135}{100}$ or $1.35$.

To find 6% of a number, we can multiply the number by $\frac{6}{100}$ or $0.06$.

Figure $\PageIndex{3}$: A triple number line with 5 tick marks. For the top number line, starting with the first tick mark, the numbers 0, the fraction 6 over 100, end fraction, times x, the fraction 49 over 100, end fraction, times x, x, and the fraction 135 over 100, end fraction, times x, are labeled. For the middle number line, starting with the first tick mark, the numbers 0, 0 point 0 6, times x, 0 point 4 9, times x, x, and 1 point 3 5, times x are labeled. For the bottom number line, starting with the first tick mark, the numbers 0, 6 percent, 49 percent, 100 percent, and 135 percent are labeled.

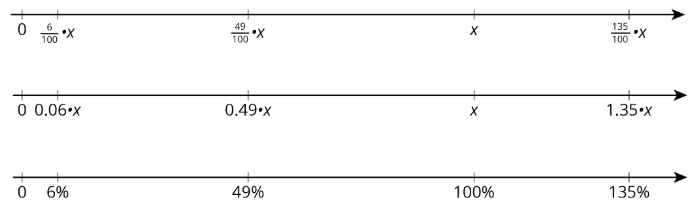
In general, to find $P$% of $x$, we can multiply: $\frac{P}{100}\cdot x$

Glossary Entries

Definition: Percent

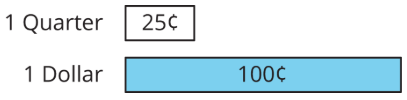
The word percent means “for each 100.” The symbol for percent is %.

For example, a quarter is worth 25 cents, and a dollar is worth 100 cents. We can say that a quarter is worth 25% of a dollar.

Figure $\PageIndex{5}$: A diagram of two bars with different lengths. The top bar is labeled 1 Quarter and 25 cents is labeled inside the bar. The bottom bar is labeled 1 Dollar. It is 4 times longer than the top bar and 100 cents is labeled inside the bar.

Definition: Percentage

A percentage is a rate per 100.

For example, a fish tank can hold 36 liters. Right now there is 27 liters of water in the tank. The percentage of the tank that is full is 75%.

Practice

Exercise $\PageIndex{4}$

To find 40% of 75, Priya calculates . Does her calculation give the correct value for 40% of 75? Explain or show how you know.
If represents a number, does always represent 40% of that number? Explain your reasoning.

Exercise $\PageIndex{5}$

Han spent 75 minutes practicing the piano over the weekend. For each question, explain or show your reasoning.

Priya practiced the violin for 152% as much time as Han practiced the piano. How long did she practice?
Tyler practiced the clarinet for 64% as much time as Han practiced the piano. How long did he practice?

Exercise $\PageIndex{6}$

Last Sunday 1,575 people visited the amusement park. 56% of the visitors were adults, 16% were teenagers, and 28% were children ages 12 and under. Find the number of adults, teenagers, and children that visited the park.

Exercise $\PageIndex{7}$

Order from greatest to least:

55% of 180
300% of 26
12% of 700

Exercise $\PageIndex{8}$

Complete each statement.

20% of 60 is ________
25% of ________ is 6
________% of 100 is 14
50% of 90 is ________
10% of ________ is 7
30% of 70 is ________

(From Unit 3.4.5)

Exercise $\PageIndex{9}$

A shopper needs 24 sandwich rolls. The store sells identical rolls in 2 differently sized packages. They sell a six-pack for $5.28 and a four-pack for $3.40. Should the shopper buy 4 six-packs or 6 four-packs? Explain your reasoning.

(From Unit 3.3.5)

Exercise $\PageIndex{10}$

On a field trip, there are 3 chaperones for every 20 students. There are 92 people on the trip. Answer these questions. If you get stuck, consider using a tape diagram.

How many chaperones are there?
How many children are there?

(From Unit 2.5.1)

Search

Text Color

Text Size

Margin Size

Font Type

	item 1	item 2	item 3	item 4	item 5
regular price	\($1\)	\($4\)	\($10\)	\($55\)	\($120\)
sale price