22.3: Using Diagrams to Find the Number of Groups
- Page ID
- 40243
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Lesson
Let's draw tape diagrams to think about division with fractions.
Exercise \(\PageIndex{1}\): How Many of These in That?
- We can think of the division expression \(10\div 2\frac{1}{2}\) as the question: “How many groups of \(2\frac{1}{2}\) are in 10?” Complete the tape diagram to represent this question. Then find the answer.
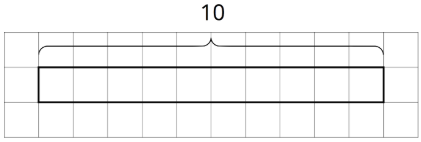
- Complete the tape diagram to represent the question: “How many groups of 2 are in 7?” Then find the answer.
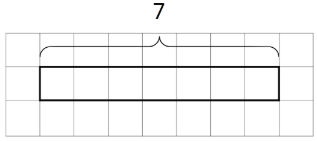
Exercise \(\PageIndex{2}\): Representing Groups of Fractions with Tape Diagrams
To make sense of the question “How many \(\frac{2}{3}\)s are in 1?,” Andre wrote equations and drew a tape diagram.
\(?\cdot\frac{2}{3}=1\)
\(1\div\frac{2}{3}=?\)
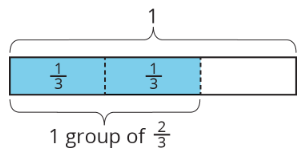
- In an earlier task, we used pattern blocks to help us solve the equation \(1\div\frac{2}{3}=?\). Explain how Andre’s tape diagram can also help us solve the equation.
- Write a multiplication equation and a division equation for each question. Then, draw a tape diagram and find the answer.
- How many \(\frac{3}{4}\)s are in \(1\)?
- How many \(\frac{2}{3}\)s are in \(3\)?
- How many \(\frac{3}{2}\)s are in \(5\)?
Exercise \(\PageIndex{3}\): Finding Number of Groups
- Write a multiplication equation or a division equation for each question. Then, find the answer and explain or show your reasoning.
- How many \(\frac{3}{8}\)-inch thick books make a stack that is 6 inches tall?
- How many groups of \(\frac{1}{2}\) pound are in \(2\frac{3}{4}\) pounds?
- Write a question that can be represented by the division equation \(5\div 1\frac{1}{2}=?\). Then, find the answer and explain or show your reasoning.
Summary
A baker used 2 kilograms of flour to make several batches of a pastry recipe. The recipe called for \(\frac{2}{5}\) kilogram of flour per batch. How many batches did she make?
We can think of the question as: “How many groups of \(\frac{2}{5}\) kilogram make 2 kilograms?” and represent that question with the equations:
\(?\cdot\frac{2}{5}=2\)
\(2\div\frac{2}{5}=?\)
To help us make sense of the question, we can draw a tape diagram. This diagram shows 2 whole kilograms, with each kilogram partitioned into fifths.
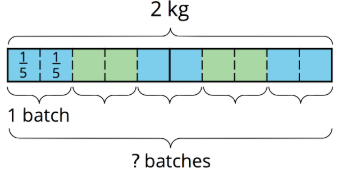
We can see there are 5 groups of \(\frac{2}{5}\) in 2. Multiplying 5 and \(\frac{2}{5}\) allows us to check this answer: \(5\cdot\frac{2}{5}=\frac{10}{5}\) and \(\frac{10}{5}=2\), so the answer is correct.
Notice the number of groups that result from \(2\div\frac{2}{5}\) is a whole number. Sometimes the number of groups we find from dividing may not be a whole number. Here is an example:
Suppose one serving of rice is \(\frac{3}{4}\) cup. How many servings are there in \(3\frac{1}{2}\) cups?
\(?\cdot\frac{3}{4}=3\frac{1}{2}\)
\(3\frac{1}{2}\div\frac{3}{4}=?\)
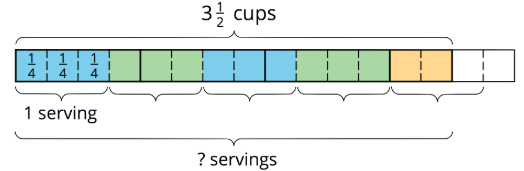
Looking at the diagram, we can see there are 4 full groups of \(\frac{3}{4}\), plus 2 fourths. If 3 fourths make a whole group, then 2 fourths make \(\frac{2}{3}\) of a group. So the number of servings (the “?” in each equation) is \(4\frac{2}{3}\). We can check this by multiplying \(4\frac{2}{3}\) and \(\frac{3}{4}\).
\(4\frac{2}{3}\cdot\frac{3}{4}=\frac{14}{3}\cdot\frac{3}{4}\), and \(\frac{14}{3}\cdot\frac{3}{4}=\frac{14}{4}\), which is indeed equivalent to \(3\frac{1}{2}\).
Practice
Exercise \(\PageIndex{4}\)
We can think of \(3\div\frac{1}{4}\) as the question “How many groups of \(\frac{1}{4}\) are in \(3\)?” Draw a tape diagram to represent this question. Then find the answer.
Exercise \(\PageIndex{5}\)
Describe how to draw a tape diagram to represent and answer \(3\div\frac{3}{5}=?\) for a friend who was absent.
Exercise \(\PageIndex{6}\)
How many groups of \(\frac{1}{2}\) day are in 1 week?
- Write a multiplication equation or a division equation to represent the question.
- Draw a tape diagram to show the relationship between the quantities and to answer the question. Use graph paper, if needed.
Exercise \(\PageIndex{7}\)
Diego said that the answer to the question “How many groups of \(\frac{5}{6}\) are in \(1\)?” is \(\frac{6}{5}\) or \(1\frac{1}{5}\). Do you agree with him? Explain or show your reasoning.
Exercise \(\PageIndex{8}\)
Select all the equations that can represent the question: “How many groups of \(\frac{4}{5}\) are in \(1\)?”
- \(?\cdot 1=\frac{4}{5}\)
- \(1\cdot\frac{4}{5}=?\)
- \(\frac{4}{5}\div 1=?\)
- \(?\cdot\frac{4}{5}=1\)
- \(1\div\frac{4}{5}=?\)
(From Unit 4.2.2)
Exercise \(\PageIndex{9}\)
Calculate each percentage mentally.
- What is \(10\)% of \(70\)?
- What is \(10\)% of \(110\)?
- What is \(25\)% of \(160\)?
- What is \(25\)% of \(48\)?
- What is \(50\)% of \(90\)?
- What is \(50\)% of \(350\)?
- What is \(75\)% of \(300\)?
- What is \(75\)% of \(48\)?
(From Unit 3.4.5)