Skip to main content
Mathematics LibreTexts

22.5: How Much in Each Group? (Part 1)

  1. Last updated
  2. Save as PDF
  • Page ID
    40241

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Lesson

    Let's look at division problems that help us find the size of one group.

    Exercise \(\PageIndex{1}\): Inventing a Situation

    1. Think of a situation with a question that can be represented by the equation \(12\div\frac{2}{3}=?\) Describe the situation and the question.
    2. Trade descriptions with your partner, and answer your partner’s question.

    Exercise \(\PageIndex{2}\): How Much in One Batch?

    To make 5 batches of cookies, 10 cups of flour are required. Consider the question: How many cups of flour does each batch require?

    We can write equations and draw a diagram to represent this situation.

    \(5\cdot ?=10\)

    \(10\div 5=?\)

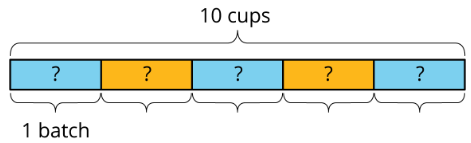
    clipboard_e21920b8db796b5c742919fd287eff7f8.png
    Figure \(\PageIndex{1}\): A tape diagram of 5 equal parts with each part labeled with a question mark. Above the diagram is a brace that represents the total labeled 10 cups. Below the diagram, 5 braces are indicated where each brace contains 1 equal part. The first of the braces is labeled 1 batch.

    This helps us see that each batch requires 2 cups of flour.

    For each question, write a multiplication equation and a division equation, draw a diagram, and find the answer.

    1. To make 4 batches of cupcakes, it takes 6 cups of flour. How many cups of flour are needed for 1 batch?
    2. To make \(\frac{1}{2}\) batch of rolls, it takes \(\frac{5}{4}\) cups of flour. How many cups of flour are needed for 1 batch?
    3. Two cups of flour make \(\frac{2}{3}\) batch of bread. How many cups of flour make 1 batch?

    Exercise \(\PageIndex{3}\): One Container and One Section of Highway

    Here are three tape diagrams that represent situations about filling containers of water.

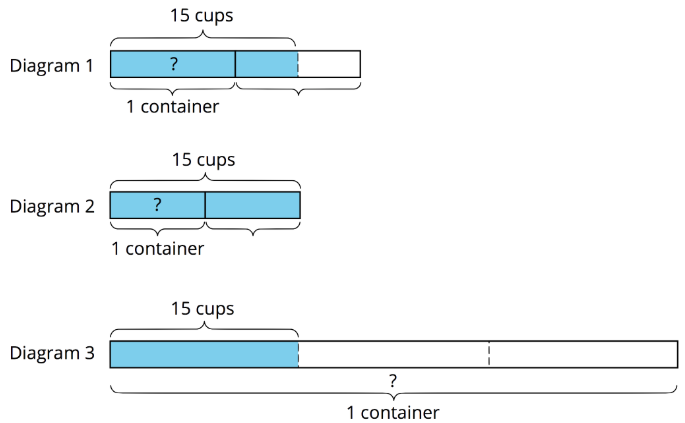
    clipboard_edd055ebf4e59b4e08c4cacb92ad10f21.png
    Figure \(\PageIndex{2}\): 3 fraction bar diagrams. Diagram 1, diagram 2, and diagram 3. Diagram 1 2 equal parts. 1 and the fraction 1 over 2 parts shaded. 1 part labeled unknown quantity and 1 container. One and the fraction 1 over 2 parts labeled 15 cups. Diagram 2, 2 equal parts. Both parts shaded. 1 part labeled unknown quantity and 1 container. Total labeled 15 cups. Diagram 3, 3 equal parts. 1 part shaded and labeled 15 cups. Total labeled the unknown quantity and 1 container.

    Match each situation to a diagram and use the diagram to help you answer the question. Then, write a multiplication equation and a division equation to represent the situation.

    1. Tyler poured a total of 15 cups of water into 2 equal-sized bottles and filled each bottle. How much water was in each bottle?
    2. Kiran poured a total of 15 cups of water into equal-sized pitchers and filled \(1\frac{1}{2}\) pitchers. How much water was in the full pitcher?
    3. It takes 15 cups of water to fill \(\frac{1}{3}\) pail. How much water is needed to fill 1 pail?

    Here are tape diagrams that represent situations about cleaning sections of highway.

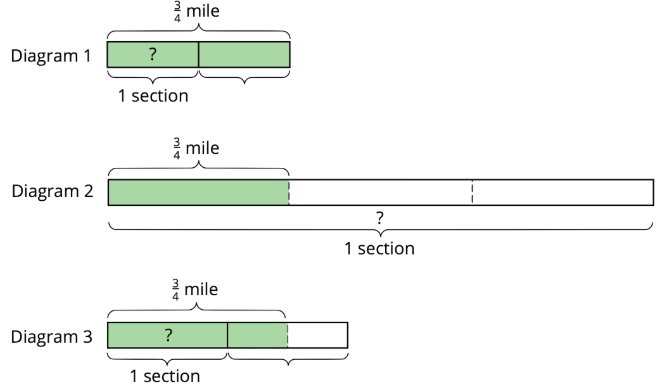
    clipboard_e08d1446a4c85a541f84330957ef7f765.png
    Figure \(\PageIndex{3}\): 3 fraction bar diagrams. Diagram 1, diagram 2, and diagram 3. Diagram 1, 2 equal parts both shaded. 1 part labeled unknown quantity and 1 section. Total labeled the fraction 3 over 4 mile. Diagram 2, 3 equal parts. 1 part shaded. 1 part labeled the fraction 3 over 4 mile. Total labeled unknown quantity and 1 section. Diagram 3, 2 equal parts. One and the fraction 1 over 2 parts shaded. 1 part labeled unknown quantity and 1 section. One and the fraction 1 over 2 parts labeled the fraction 3 over 4 mile.

    Match each situation to a diagram and use the diagram to help you answer the question. Then, write a multiplication equation and a division equation to represent the situation.

    1. Priya’s class has adopted two equal sections of a highway to keep clean. The combined length is \(\frac{3}{4}\) of a mile. How long is each section?
    2. Lin’s class has also adopted some sections of highway to keep clean. If \(1\frac{1}{2}\) sections are \(\frac{3}{4}\) mile long, how long is each section?
    3. A school has adopted a section of highway to keep clean. If \(\frac{1}{3}\) of the section is \(\frac{3}{4}\) mile long, how long is the section?

    Are you ready for more?

    To make a Cantor ternary set:

    • Start with a tape diagram of length 1 unit. This is step 1.
    • Color in the middle third of the tape diagram. This is step 2.
    • Do the same to each remaining segment that is not colored in. This is step 3.
    • Keep repeating this process.
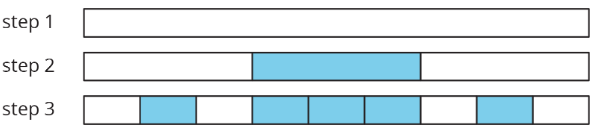
    clipboard_efca21abe5c3fc22a029198cee11685b0.png
    Figure \(\PageIndex{4}\): Three tape diagrams of equal length, step 1, step 2, and step 3. step 1 is a solid white bar. step 2 is divided into 3 equal parts. Second part is shaded blue. step 3 is divided into 9 equal parts. The second, fourth, fifth, sixth, and eighth parts are shaded blue.
    1. How much of the diagram is colored in after step 2? Step 3? Step 10?
    2. If you continue this process, how much of the tape diagram will you color?
    3. Can you think of a different process that will give you a similar result? For example, color the first fifth instead of the middle third of each strip.

    Summary

    Sometimes we know the amount for multiple groups, but we don’t know how much is in one group. We can use division to find out.

    For example, if 5 people share \(8\frac{1}{2}\) pounds of cherries equally, how many pounds of cherries does each person get?

    clipboard_e29e650689b34c7d17e5988b93b24cd90.png
    Figure \(\PageIndex{5}\): A fraction bar diagram. 5 equal parts. Each part labeled unknown quantity. 1 part labeled 1 person. Total labeled 8 and one half pounds and 5 people.

    We can represent this situation with a multiplication equation and a division equation:

    \(5\cdot ?=8\frac{1}{2}\)

    \(8\frac{1}{2}\div 5=?\)

    \(8\frac{1}{2}\div 5\) can be written as \(\frac{17}{2}\div 5\). Dividing by 5 is equivalent to multiplying by \(\frac{1}{5}\), and \(\frac{17}{2}\cdot\frac{1}{5}=\frac{17}{10}\). This means each person gets \(1\frac{7}{10}\) pounds.

    Other times, we know the amount for a fraction of a group, but we don’t know the size of one whole group. We can also use division to find out.

    For example, Jada poured 5 cups of iced tea in a pitcher and filled \(\frac{2}{3}\) of the pitcher. How many cups of iced tea fill the entire pitcher?

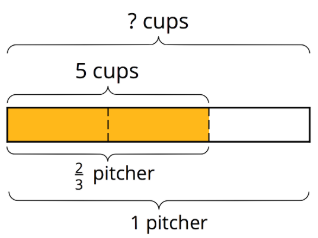
    clipboard_e25849ff4bcf6ad8380f93a4ec2d8d1b1.png
    Figure \(\PageIndex{6}\): A fraction bar diagram. 3 equal parts. 2 parts shaded and labeled 5 cups and the fraction 2 over 3 pitcher. Total labeled unknown quantity cups and 1 pitcher.

    We can represent this situation with a multiplication equation and a division equation:

    \(\frac{2}{3}\cdot ?=5\)

    \(5\div\frac{2}{3}=?\)

    The diagram can help us reason about the answer. If \(\frac{2}{3}\) of a pitcher is 5 cups, then \(\frac{1}{3}\) of a pitcher is half of 5, which is \(\frac{5}{2}\). Because there are 3 thirds in 1 whole, there would be \((3\cdot\frac{5}{2})\) or \(\frac{15}{2}\) cups in one whole pitcher. We can check our answer by multiplying: \(\frac{2}{3}\cdot\frac{15}{2}=\frac{30}{6}\), and \(\frac{30}{6}=5\).

    Notice that in the first example, the number of groups is greater than 1 (5 people) and in the second, the number of groups is less than 1 (\(\frac{2}{3}\) of a pitcher), but the division and multiplication equations for both situations have the same structures.

    Practice

    Exercise \(\PageIndex{4}\)

    For each situation, complete the tape diagram to represent and answer the question.

    1. Mai has picked 1 cup of strawberries for a cake, which is enough for \(\frac{3}{4}\) of the cake. How many cups does she need for the whole cake?
    clipboard_e0b2800e0a76fa8300f1fdf70163ce849.png
    Figure \(\PageIndex{7}\)
    1. Priya has picked \(1\frac{1}{2}\) cups of raspberries, which is enough for \(\frac{3}{4}\) of a cake. How many cups does she need for the whole cake?
    clipboard_e0b2800e0a76fa8300f1fdf70163ce849.png
    Figure \(\PageIndex{8}\)

    Exercise \(\PageIndex{5}\)

    Consider the problem: Tyler painted \(\frac{9}{2}\) square yards of wall area with \(3\) gallons of paint. How many gallons of paint does it take to paint each square yard of wall?

    1. Write multiplication and division equations to represent the situation.
    2. Draw a diagram to represent and answer the question.

    Exercise \(\PageIndex{6}\)

    Consider the problem: After walking \(\frac{1}{4}\) mile from home, Han is \(\frac{1}{3}\) of his way to school. What is the distance between his home and school?

    1. Write multiplication and division equations to represent this situation.
    2. Complete the diagram to represent and answer the question.
    clipboard_e83d4fde9e42516a22af9fc9c67e8477c.png
    Figure \(\PageIndex{9}\)

    Exercise \(\PageIndex{7}\)

    Here is a division equation: \(\frac{4}{5}\div\frac{2}{3}=?\)

    1. Write a multiplication equation that corresponds to the division equation.
    2. Draw a diagram to represent and answer the question.

    (From Unit 4.2.4)

    Exercise \(\PageIndex{8}\)

    Consider the problem: A set of books that are each 1.5 inches wide are being organized on a bookshelf that is 36 inches wide. How many books can fit on the shelf?

    1. Write multiplication and division equations to represent the situation.
    2. Find the answer. Draw a diagram, if needed.
    3. Use the multiplication equation to check your answer.

    (From Unit 4.1.3)

    Exercise \(\PageIndex{9}\)

    1. Without calculating, order the quotients from smallest or largest.
      \[\begin{array}{ccccc}{56\div 8}&{\qquad}&{56\div 8,000,000}&{\qquad}&{56\div 0.000008}\end{array}\nonumber\]
    2. Explain how you decided the order of the three expressions.
    3. Find a number \(n\) so that \(56\div n\) is greater than 1 but less than 7.

    (From Unit 4.1.1)

    22.5: How Much in Each Group? (Part 1) is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      License
      CC BY
      License Version
      4.0
    2. Tags
      This page has no tags.