29.3: Dividing Numbers that Result in Decimals

Last updated
Save as PDF

Page ID: 40308

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's find quotients that are not whole numbers.

Exercise $\PageIndex{1}$: Number Talk: Evaluationg Quotients

Find the quotients mentally.

$400\div 8$

$80\div 8$

$16\div 8$

$496\div 8$

Exercise $\PageIndex{2}$: Keep Dividing

Mai used base-ten diagrams to calculate $62\div 5$. She started by representing $62$.

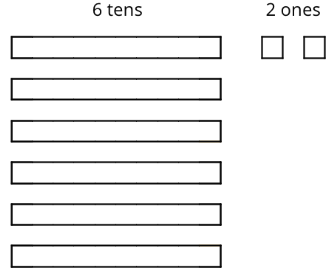
She then made 5 groups, each with 1 ten. There was 1 ten left. She unbundled it into 10 ones and distributed the ones across the 5 groups.

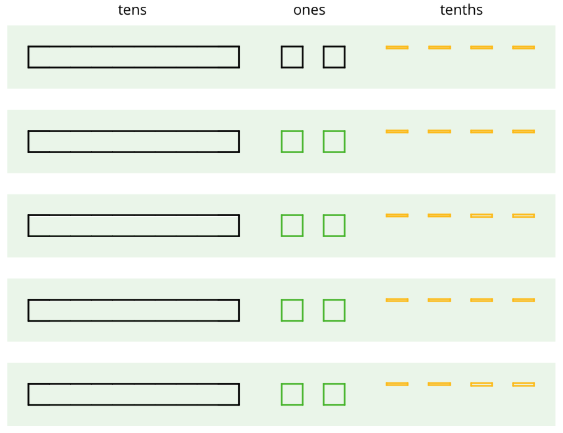
Here is Mai’s diagram for $62\div 5$.

Discuss these questions with a partner and write down your answers:
1. Mai should have a total of 12 ones, but her diagram shows only 10. Why?
2. She did not originally have tenths, but in her diagram each group has 4 tenths. Why?
3. What value has Mai found for $62\div 5$? Explain your reasoning.
Find the quotient of $511\div 5$ by drawing base-ten diagrams or by using the partial quotients method. Show your reasoning. If you get stuck, work with your partner to find a solution.
Four students share a $271 prize from a science competition. How much does each student get if the prize is shared equally? Show your reasoning.

Exercise $\PageIndex{3}$: Using Long Division to Calculate Quotients

Here is how Lin calculated $62\div 5$.

Figure $\PageIndex{3}$: Long division calculation of 62 divided by 5, 4 steps. Step 1, 1 row. First row: 5, long division symbol with 62 inside. Step 2, 6 rows. First row: 1, second row: 5, long division symbol with 62 inside, third row: minus 5, horizontal line, fourth row: 12, fifth row: minus 10, horizontal line, sixth row: 2. Step 3, 6 rows. First row: 12, second row: 5, long division symbol with 62 inside, third row: minus 5, horizontal line, fourth row: 12, fifth row: minus 10, horizontal line, sixth row: 2 point 0. Step 4, 8 rows. First row: 12 point 4, second row: 5, long division symbol with 62 inside, third row: minus 5, horizontal line, fourth row: 12, fifth row: minus 10, horizontal line, sixth row: 2 point 0, seventh row: minus 2 point 0, horizontal line, eighth row: 0.

Discuss with your partner:
- Lin put a 0 after the remainder of 2. Why? Why does this 0 not change the value of the quotient?
- Lin subtracted 5 groups of 4 from 20. What value does the 4 in the quotient represent?
- What value did Lin find for $62\div 5$?
Use long division to find the value of each expression. Then pause so your teacher can review your work.
1. $126\div 8$
2. $90\div 12$
Use long division to show that:
1. $5\div 4$, or $\frac{5}{4}$, is $1.25$.
2. $4\div 5$, or $\frac{4}{5}$, is $0.8$.
3. $1\div 8$, or $\frac{1}{8}$, is $0.125$.
4. $1\div 25$, or $\frac{1}{25}$, is $0.04$.
Noah said we cannot use long division to calculate $10\div 3$ because there will always be a remainder.
1. What do you think Noah meant by “there will always be a remainder”?
2. Do you agree with him? Explain your reasoning.

Summary

Dividing a whole number by another whole number does not always produce a whole-number quotient. Let’s look at $86\div 4$, which we can think of as dividing 86 into 4 equal groups.

Figure $\PageIndex{4}$: 4 groups of base-ten diagrams. Each group contains 2 rectangles labeled, tens, and 1 square labeled, ones. 2 squares are unbundled into 20 small rectangles labeled, tenths.

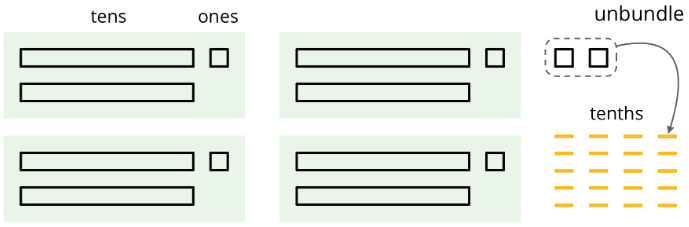
We can see in the base-ten diagram that there are 4 groups of 21 in 86 with 2 ones left over. To find the quotient, we need to distribute the 2 ones into the 4 groups. To do this, we can unbundle or decompose the 2 ones into 20 tenths, which enables us to put 5 tenths in each group.

Once the 20 tenths are distributed, each group will have 2 tens, 1 one, and 5 tenths, so $86\div 4=21.5$.

Figure $\PageIndex{5}$: Long division calculation of 86 divided by 4. 8 rows. First row: 21 point 5, Second row: 4, long division symbol with 86 inside. Third row: minus 8. Horizontal line. Fourth row: 6. Fifth row: minus 4. Horizontal line. Sixth row: 2 point 0. Seventh row: minus 2 point 0. Horizontal line. Eighth row: 0.

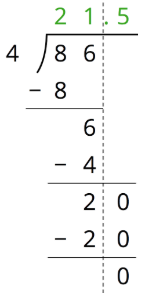
We can also calculate $86\div 4$ using long division.

The calculation shows that, after removing 4 groups of 21, there are 2 ones remaining. We can continue dividing by writing a 0 to the right of the 2 and thinking of that remainder as 20 tenths, which can then be divided into 4 groups.

To show that the quotient we are working with now is in the tenth place, we put a decimal point to the right of the 1 (which is in the ones place) at the top. It may also be helpful to draw a vertical line to separate the ones and the tenths.

There are 4 groups of 5 tenths in 20 tenths, so we write 5 in the tenths place at the top. The calculation likewise shows $86\div 4=21.5$.

Glossary Entries

Definition: Long Division

Long division is a way to show the steps for dividing numbers in decimal form. It finds the quotient one digit at a time, from left to right.

For example, here is the long division for $57\div 4$.

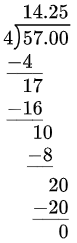
Practice

Exercise $\PageIndex{4}$

Use long division to show that the fraction and decimal in each pair are equal.

$\frac{3}{4}$ and $0.75\qquad\frac{3}{50}$ and $0.06\qquad\frac{7}{25}$ and $0.28$

Exercise $\PageIndex{5}$

Mai walked $\frac{1}{8}$ of a 30-mile walking trail. How many miles did Mai walk? Explain or show your reasoning.

Exercise $\PageIndex{6}$

Use long division to find each quotient. Write your answer as a decimal.

$99\div 12$
$216\div 5$
$1,988\div 8$

Exercise $\PageIndex{7}$

Tyler reasoned: “$\frac{9}{25}$ is equivalent to $\frac{18}{50}$ and to $\frac{36}{100}$, so the decimal of $\frac{9}{25}$ is 0.36.”

Use long division to show that Tyler is correct.
Is the decimal of $\frac{18}{50}$ also $0.36$? Use long division to support your answer.

Exercise $\PageIndex{8}$

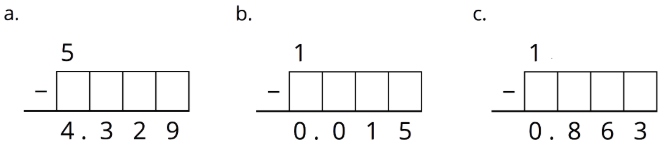
Complete the calculations so that each shows the correct difference.

Figure $\PageIndex{7}$: Fill in the blank subtraction problem a. 5 minus blank blank blank blank equals 4 point 329. Fill in the blank subtraction problem b. 1 minus blank blank blank blank equals 0 point 015. Fill in the blank subtraction problem c. 1 minus blank blank blank blank equals 0 point 863.

(From Unit 5.2.3)

Exercise $\PageIndex{9}$

Use the equation $124\cdot 15=1,860$ and what you know about fractions, decimals, and place value to explain how to place the decimal point when you compute $(1.24)\cdot (0.15)$

(From Unit 5.3.2)

Search

Text Color

Text Size

Margin Size

Font Type