29.4: Dividing Decimals by Whole Numbers

Last updated
Save as PDF

Page ID: 40307

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's divide decimals by whole numbers.

Exercise $\PageIndex{1}$: Number Talk: Dividing by $4$

Find each quotient mentally.

$80\div 4$

$12\div 4$

$1.2\div 4$

$81.2\div 4$

Exercise $\PageIndex{2}$: Using Diagrams to Represent Division

To find $53.8\div 4$ using diagrams, Elena began by representing 53.8.

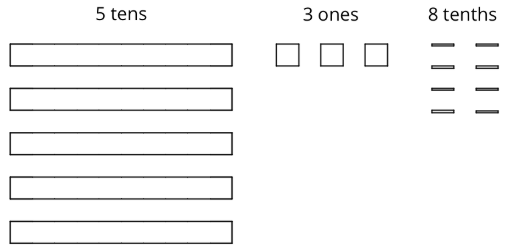
She placed 1 ten into each group, unbundled the remaining 1 ten into 10 ones, and went on distributing the units.

This diagram shows Elena’s initial placement of the units and the unbundling of 1 ten.

Figure $\PageIndex{2}$: 4 groups of base-ten diagrams. Group 1, 1 rectangle labeled, tens, 1 square labeled, ones, 2 small rectangles labeled, tenths. Group 2, 1 rectangle labeled, tens, 1 square labeled, ones, 2 small rectangles labeled, tenths. Group 3, 1 rectangle labeled, tens, 1 square labeled, ones, 2 small rectangles labeled, tenths. Group 4, 1 rectangle labeled, tens, 2 small rectangles labeled, tenths. Below, 1 rectangle is unbundled into 10 squares.

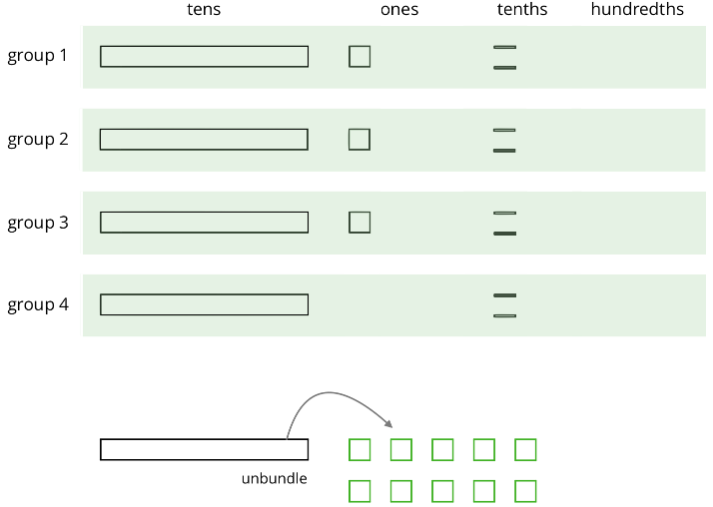
Complete the diagram by continuing the division process. How would you use the available units to make 4 equal groups?
As the units get placed into groups, show them accordingly and cross out those pieces from the bottom. If you unbundle a unit, draw the resulting pieces.
What value did you find for $53.8\div 4$? Be prepared to explain your reasoning.
Use long division to find $53.8\div 4$. Check your answer by multiplying it by the divisor 4.
Use long division to find $77.4\div 5$. If you get stuck, you can draw diagrams or use another method.

Are you ready for more?

A distant, magical land uses jewels for their bartering system. The jewels are valued and ranked in order of their rarity. Each jewel is worth 3 times the jewel immediately below it in the ranking. The ranking is red, orange, yellow, green, blue, indigo, and violet. So a red jewel is worth 3 orange jewels, a green jewel is worth 3 blue jewels, and so on.

A group of 4 craftsmen are paid 1 of each jewel. If they split the jewels evenly amongst themselves, which jewels does each craftsman get?

Exercise $\PageIndex{3}$: Dividends and Divisors

Analyze the dividends, divisors, and quotients in the calculations, and then answer the questions.

Figure $\PageIndex{3}$: 4 long division calculations. 72 divided by 3, 720 divided by 30, 7,200 divided by 300, and 72,000 divided by 3,000. First calculation, 6 rows. First row: 24. Second row: 3, long division symbol with 72 inside. Third row: minus 6. Horizontal line. Fourth row: 12. Fifth row: minus 12. Horizontal line. Sixth row: 0. Second calculation, 6 rows. First row: 24. Second row: 30, long division symbol with 720 inside. Third row: minus 60. Horizontal line. Fourth row: 120. Fifth row: minus 120. Horizontal line. Sixth row: 0. Third calculation, 6 rows. First row: 24. Second row: 300, long division symbol with 7,200 inside. Third row: minus 600. Horizontal line. Fourth row: 1,200. Fifth row: minus 1,200. Horizontal line. Sixth row: 0. Fourth calculation, 6 rows. First row: 24. Second row: 3,000, long division symbol with 72,000 inside. Third row: minus 6,000. Horizontal line. Fourth row: 12,000. Fifth row: minus 12,000. Horizontal line. Sixth row: 0.

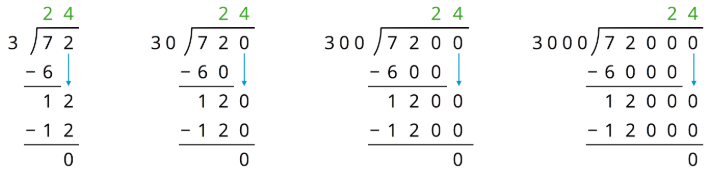
Complete each sentence. In the calculations shown:
- Each dividend is ______ times the dividend to the left of it.
- Each divisor is ______ times the divisor to the left of it.
- Each quotient is _____________________ the quotient to the left of it.
Suppose we are writing a calculation to the right of $72,000\div 3,000$. Which expression has a quotient of 24? Be prepared to explain your reasoning.
1. $72,000\div 30,000$
2. $720,000\div 300,000$
3. $720,000\div 30,000$
4. $720,000\div 3,000$
Suppose we are writing a calculation to the left of $72\div 3$. Write an expression that would also give a quotient of 24. Be prepared to explain your reasoning.
Decide which of the following expressions would have the same value as $250\div 10$. Be prepared to share your reasoning.
1. $250\div 0.1$
2. $25\div 1$
3. $2.5\div 1$
4. $2.5\div 0.1$
5. $2,500\div 100$
6. $0.25\div 0.01$

Summary

We know that fractions such as $\frac{6}{4}$ and $\frac{60}{40}$ are equivalent because:

The numerator and denominator of are each 10 times those of $\frac{6}{4}$.
Both fractions can be simplified to $\frac{3}{2}$.
600 divided by 400 is 1.5, and 60 divided by 40 is also 1.5.

Just like fractions, division expressions can be equivalent. For example, the expressions $540\div 90$ and $5,400\div 900$ are both equivalent to $54\div 9$ because:

They all have a quotient of 6.
The dividend and the divisor in $540\div 90$ are each 10 times the dividend and divisor in $54\div 9$. Those in $5,400\div 900$ are each 100 times the dividend and divisor in $54\div 90$. In both cases, the quotient does not change.

This means that an expression such as $5.4\div 0.9$ also has the same value as $54\div 9$. Both the dividend and divisor of $5.4\div 0.9$ are $\frac{1}{10}$ of those in $54\div 9$.

In general, multiplying a dividend and a divisor by the same number does not change the quotient. Multiplying by powers of 10 (e.g., 10, 100, 1,000, etc.) can be particularly useful for dividing decimals, as we will see in an upcoming lesson.

Glossary Entries

Definition: Long Division

Long division is a way to show the steps for dividing numbers in decimal form. It finds the quotient one digit at a time, from left to right.

For example, here is the long division for $57\div 4$.

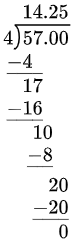
Practice

Exercise $\PageIndex{4}$

Here is a diagram representing a base-ten number. The large rectangle represents a unit that is 10 times the value of the square. The square represents a unit that is 10 times the value of the small rectangle.

Here is a diagram showing the number being divided into 5 equal groups.

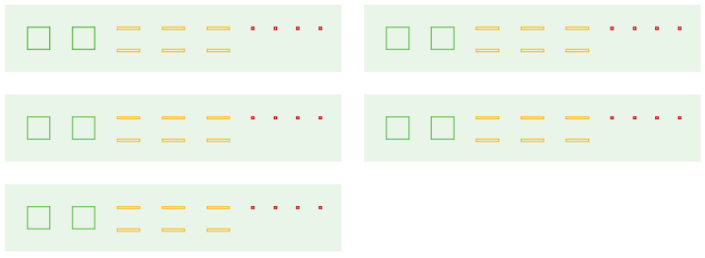
If a large rectangle represents 1,000, what division problem did the second diagram show? What is its answer?
If a large rectangle represents 100, what division problem did the second diagram show? What is its answer?
If a large rectangle represents 10, what division problem did the second diagram show? What is its answer?

Exercise $\PageIndex{5}$

Explain why all of these expressions have the same value.

$4.5\div 0.09\qquad 45\div 0.9\qquad 450\div 9\qquad 4500\div 90$

What is the common value?

Exercise $\PageIndex{6}$

Use long division to find each quotient.

$7.89\div 2$
$39.54\div 3$
$0.176\div 5$

Exercise $\PageIndex{7}$

Four students set up a lemonade stand. At the end of the day, their profit is $17.52. How much money do they each have when the profit is split equally? Show or explain your reasoning.

Exercise $\PageIndex{8}$

A standard sheet of paper in the United States is 11 inches long and 8.5 inches wide. Each inch is 2.54 centimeters. How long and wide is a standard sheet of paper in centimeters?
A standard sheet of paper in Europe is 21.0 cm wide and 29.7 cm long. Which has the greater area, the standard sheet of paper in the United States or the standard sheet of paper in Europe? Explain your reasoning.

(From Unit 5.3.4)

Search

Text Color

Text Size

Margin Size

Font Type