34.1: Two Related Quantities, Part 1

Last updated
Save as PDF

Page ID: 40620

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's use equations and graphs to describe relationships with ratios.

Exercise $\PageIndex{1}$: Which One Would You Choose?

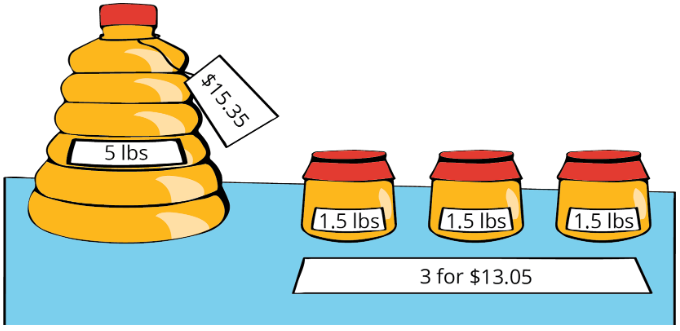
Which one would you choose? Be prepared to explain your reasoning.

A 5-pound jug of honey for $15.35
Three 1.5-pound jars of honey for $13.05

Exercise $\PageIndex{2}$: Painting the Set

Lin needs to mix a specific shade of orange paint for the set of the school play. The color uses 3 parts yellow for every 2 parts red.

Complete the table to show different combinations of red and yellow paint that will make the shade of orange Lin needs.

Table $\PageIndex{1}$
cups of red paint ($r$)	cups of yellow paint ($y$)	total cups of paint ($t$)
$2$	$3$
$6$
		$20$
	$18$
$14$
$16$
		$50$
	$42$

Lin notices that the number of cups of red paint is always $\frac{2}{5}$ of the total number of cups. She writes the equation $r=\frac{2}{5}t$ to describe the relationship. Which is the independent variable? Which is the dependent variable? Explain how you know.
Write an equation that describes the relationship between $r$ and $y$ where $y$ is the independent variable.
Write an equation that describes the relationship between $y$ and $r$ where $r$ is the independent variable.
Use the points in the table to create two graphs that show the relationship between $r$ and $y$. Match each relationship to one of the equations you wrote.

Are you ready for more?

A fruit stand sells apples, peaches, and tomatoes. Today, they sold 4 apples for every 5 peaches. They sold 2 peaches for every 3 tomatoes. They sold 132 pieces of fruit in total. How many of each fruit did they sell?

Summary

Equations are very useful for describing sets of equivalent ratios. Here is an example.

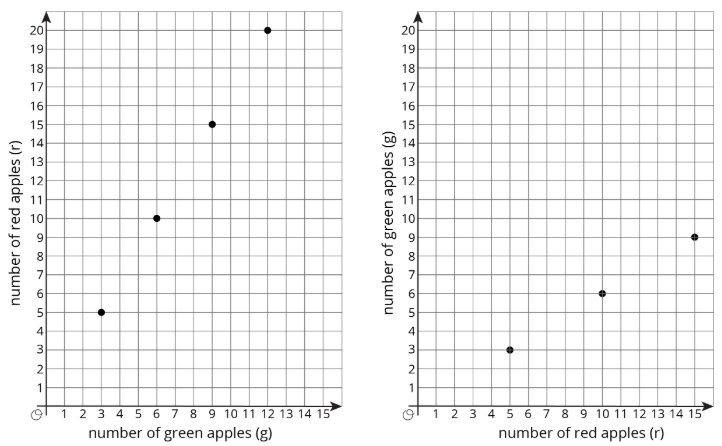
A pie recipe calls for 3 green apples for every 5 red apples. We can create a table to show some equivalent ratios.

We can see from the table that $r$ is always $\frac{5}{3}$ as large as $g$ and that $g$ is always $\frac{3}{5}$ as large as $r$.

green apples ($g$)	red apples ($r$)
$3$	$5$
$6$	$10$
$9$	$15$
$12$	$20$

Table$\PageIndex{2}$

We can write equations to describe the relationship between $g$ and $r$.

When we know the number of green apples and want to find the number of red apples, we can write:

$r=\frac{5}{3}g$

In this equation, if $g$ changes, $r$ is affected by the change, so we refer to $g$ as the independent variable and $r$ as the dependent variable.

We can use this equation with any value of $g$ to find $r$. If 270 green apples are used, then $\frac{5}{3}\cdot (270)$ or 450 red apples are used.

When we know the number of red apples and want to find the number of green apples, we can write:

$g=\frac{3}{5}r$

In this equation, if $r$ changes, $g$ is affected by the change, so we refer to $r$ as the independent variable and $g$ as the dependent variable.

We can use this equation with any value of $r$ to find $g$. If 275 red apples are used, then $\frac{3}{5}\cdot (275)$ or 165 green apples are used.

We can also graph the two equations we wrote to get a visual picture of the relationship between the two quantities.

Figure $\PageIndex{2}$: Two graphs that represent a ratio of two quantities. The graph on the left has a horizontal axis labeled number of green apples and the numbers 1 through 15 are indicated, The vertical axis is labeled number of red apples and the numbers 1 through 20 are indicated. The following four points are indicated on the graph: 3 comma 5, 6 comma 10, 9 comma 15, and 12 comma 20. The graph on the right has a horizontal axis labeled number of red apples and the numbers 1 through 15 are indicated. The vertical axis is labeled number of green apples and the numbers 1 through 20 are indicated. The following three points are indicated on the graph: 5 comma 3, 10 comma 6, and 15 comma 9.

Glossary Entries

Definition: Dependent Variable

The dependent variable is the result of a calculation.

For example, a boat travels at a constant speed of 25 miles per hour. The equation $d=25t$ describes the relationship between the boat's distance and time. The dependent variable is the distance traveled, because $d$ is the result of multiplying 25 by $t$.

Figure $\PageIndex{3}$: A graph of 10 points plotted in the coordinate plane with the origin labeled O. The horizontal t axis is labeled time in hours. The numbers 0 through 10, in increments of 2, are indicated, and there are vertical grid lines midway between. The vertical axis is labeled distance traveled in miles. The numbers 0 through 250, in increments of 25, are indicated, and there are horizontal grid lines midway between. The data are as follows: 1 comma 25. 2 comma 50. 3 comma 75. 4 comma 100. 5 comma 125. 6 comma 150. 7 comma 175. 8 comma 200. 9 comma 225. 10 comma 250.

Definition: Independent Variable

The independent variable is used to calculate the value of another variable.

For example, a boat travels at a constant speed of 25 miles per hour. The equation $d=25t$ describes the relationship between the boat's distance and time. The independent variable is time, because $t$ is multiplied by 25 to get $d$.

Figure $\PageIndex{4}$: A graph of 10 points plotted in the coordinate plane with the origin labeled O. The horizontal t axis is labeled time in hours. The numbers 0 through 10, in increments of 2, are indicated, and there are vertical grid lines midway between. The vertical axis is labeled distance traveled in miles. The numbers 0 through 250, in increments of 25, are indicated, and there are horizontal grid lines midway between. The data are as follows: 1 comma 25. 2 comma 50. 3 comma 75. 4 comma 100. 5 comma 125. 6 comma 150. 7 comma 175. 8 comma 200. 9 comma 225. 10 comma 250.

Practice

Exercise $\PageIndex{3}$

Here is a graph that shows some values for the number of cups of sugar, $s$, required to make $x$ batches of brownies.

Figure $\PageIndex{5}$: Eight points plotted on the coordinate plane with the origin labeled O. The x axis is labeled batches of brownies and the numbers 0 through 8 are indicated. The s axis is labeled cups of sugar and the numbers 0 through 6 are indicated. There are horizontal grid lines halfway between each integer. The data are as follows: 1 comma one half. 2 comma 1. 3 comma one and one half. 4 comma 2. 5 comma 2 and one half. 6 comma 3. 7 comma 3 and one half. 8 comma 4.

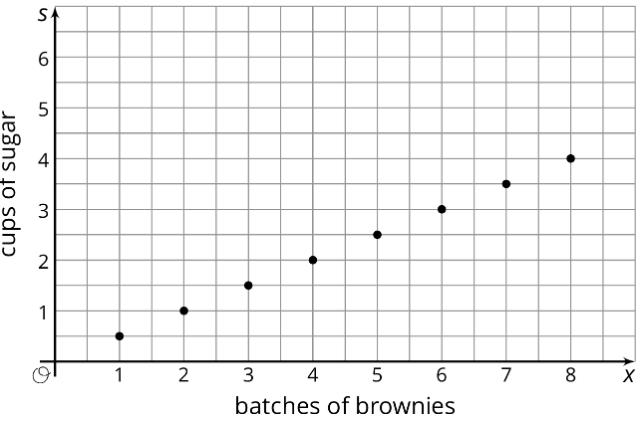
Complete the table so that the pair of numbers in each column represents the coordinates of a point on the graph.

Table $\PageIndex{3}$
$x$	$1$	$2$	$3$	$4$	$5$	$6$	$7$
$s$

What does the point $(8,4)$ mean in terms of the amount of sugar and number of batches of brownies?
Write an equation that shows the amount of sugar in terms of the number of batches.

Exercise $\PageIndex{4}$

Each serving of a certain fruit snack contains 90 calories.

Han wants to know how many calories he gets from the fruit snacks. Write an equation that shows the number of calories, $c$, in terms of the number of servings, $n$.
Tyler needs some extra calories each day during his sports season. He wants to know how many servings he can have each day if all the extra calories come from the fruit snack. Write an equation that shows the number of servings, $n$, in terms of the number of calories, $c$.

Exercise $\PageIndex{5}$

Kiran shops for books during a 20% off sale.

What percent of the original price of a book does Kiran pay during the sale?
Complete the table to show how much Kiran pays for books during the sale.
Write an equation that relates the sale price, $s$, to the original price $p$.
On graph paper, create a graph showing the relationship between the sale price and the original price by plotting the points from the table.

Table $\PageIndex{4}$
original price in dollars ($p$)	sale price in dollars ($s$)
$1$
$2$
$3$
$4$
$5$
$6$
$7$
$8$
$9$
$10$

Exercise $\PageIndex{6}$

Evaluate each expression when $x$ is $4$ and $y$ is $6$.

$(6-x)^{3}+y$
$2+x^{3}$
$2^{x}-2y$
$\left(\frac{1}{2}\right)^{x}$
$1^{x}+2^{x}$
$\frac{2^{x}}{x^{2}}$

(From Unit 6.3.4)

Exercise $\PageIndex{7}$

Find $(12.34)\cdot (0.7)$. Show your reasoning.

(From Unit 5.3.4)

Exercise $\PageIndex{8}$

For each expression, write another division expression that has the same value and that can be used to help find the quotient. Then, find each quotient.

$302.1\div 0.5$
$12.15\div 0.02$
$1.375\div 0.11$

(From Unit 5.4.5)

cups of red paint (\(r\))	cups of yellow paint (\(y\))	total cups of paint (\(t\))
\(2\)	\(3\)
\(6\)
		\(20\)
	\(18\)
\(14\)
\(16\)
		\(50\)
	\(42\)

green apples (\(g\))	red apples (\(r\))
\(3\)	\(5\)
\(6\)	\(10\)
\(9\)	\(15\)
\(12\)	\(20\)

\(x\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)	\(7\)
\(s\)

original price in dollars (\(p\))	sale price in dollars (\(s\))
\(1\)
\(2\)
\(3\)
\(4\)
\(5\)
\(6\)
\(7\)
\(8\)
\(9\)
\(10\)

Search

Text Color

Text Size

Margin Size

Font Type