1.2: Finding Area by Decomposing and Rearranging
( \newcommand{\kernel}{\mathrm{null}\,}\)
Lesson
Let's create shapes and find their areas.
Exercise 1.2.1: What is Area?
You may recall that the term area tells us something about the number of squares inside a two-dimensional shape.
- Here are four drawings that each show squares inside a shape. Select all drawings whose squares could be used to find the area of the shape. Be prepared to explain your reasoning.
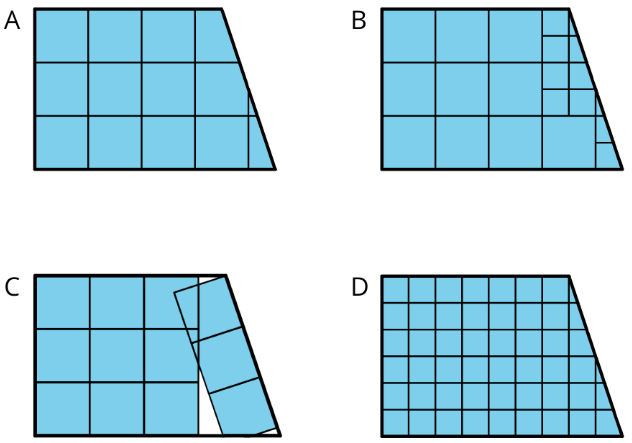
- Write a definition of area that includes all the information that you think is important.
Exercise 1.2.2: Composing Shapes
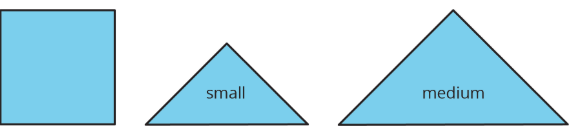
This applet has one square and some small, medium, and large right triangles. The area of the square is 1 square unit.
Click on a shape and drag to move it. Grab the point at the vertex and drag to turn it.
- Notice that you can put together two small triangles to make a square. What is the area of the square composed of two small triangles? Be prepared to explain your reasoning.
- Use your shapes to create a new shape with an area of 1 square unit that is not a square. Draw your shape on paper and label it with its area.
- Use your shapes to create a new shape with an area of 2 square units. Draw your shape and label it with its area.
- Use your shapes to create a different shape with an area of 2 square units. Draw your shape and label it with its area.
- Use your shapes to create a new shape with an area of 4 square units. Draw your shape and label it with its area.
Are you ready for more?
Find a way to use all of your pieces to compose a single large square. What is the area of this large square?
Exercise 1.2.3: Tangram Triangles
Recall that the area of the square you saw earlier is 1 square unit. Complete each statement and explain your reasoning.
- The area of the small triangle is ____________ square units. I know this because . . .
- The area of the medium triangle is ____________ square units. I know this because . . .
- The area of the large triangle is ____________ square units. I know this because . . .
Summary
Here are two important principles for finding area:
- If two figures can be placed one on top of the other so that they match up exactly, then they have the same area.
- We can decompose a figure (break a figure into pieces) and rearrange the pieces (move the pieces around) to find its area.
Here are illustrations of the two principles.
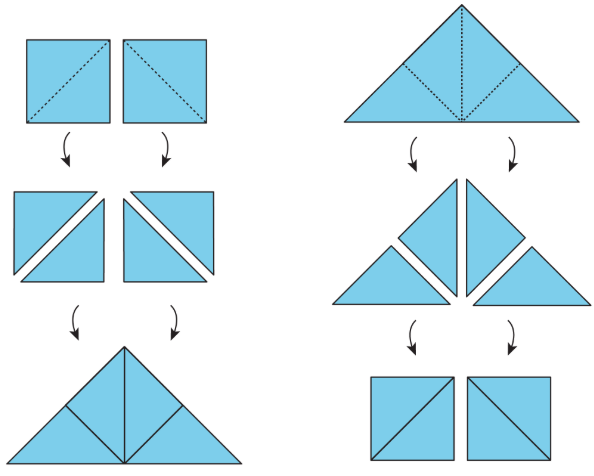
- Each square on the left can be decomposed into 2 triangles. These triangles can be rearranged into a large triangle. So the large triangle has the same area as the 2 squares.
- Similarly, the large triangle on the right can be decomposed into 4 equal triangles. The triangles can be rearranged to form 2 squares. If each square has an area of 1 square unit, then the area of the large triangle is 2 square units. We also can say that each small triangle has an area of 12 square unit.
Glossary Entries
Definition: Area
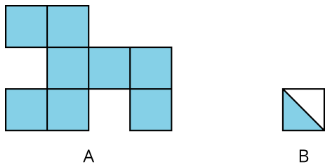
Area is the number of square units that cover a two-dimensional region, without any gaps or overlaps.
For example, the area of region A is 8 square units. The area of the shaded region of B is 12 square unit.
Definition: Compose
Compose means “put together.” We use the word compose to describe putting more than one figure together to make a new shape.
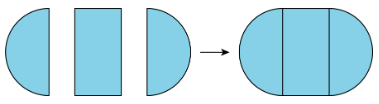
Definition: Decompose
Decompose means “take apart.” We use the word decompose to describe taking a figure apart to make more than one new shape.
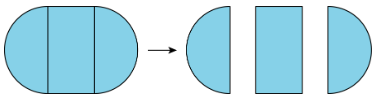
Definition: Region
A region is the space inside of a shape. Some examples of two-dimensional regions are inside a circle or inside a polygon. Some examples of three-dimensional regions are the inside of a cube or the inside of a sphere.
Practice
Exercise 1.2.4
The diagonal of a rectangle is shown.
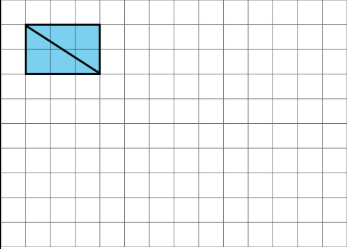
- Decompose the rectangle along the diagonal, and recompose the two pieces to make a different shape.
- How does the area of this new shape compare to the area of the original rectangle? Explain how you know.
Exercise 1.2.5
Priya decomposed a square into 16 smaller, equal-size squares and then cut out 4 of the small squares and attached them around the outside of original square to make a new figure.
How does the area of her new figure compare with that of the original square?
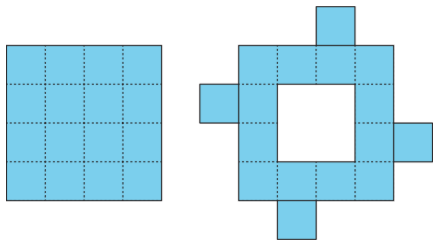
- The area of the new figure is greater.
- The two figures have the same area.
- The area of the original square is greater.
- We don’t know because neither the side length nor the area of the original square is known.
Exercise 1.2.6
The area of the square is 1 square unit. Two small triangles can be put together to make a square or to make a medium triangle.
Which figure also has an area of 112 square units? Select all that apply.
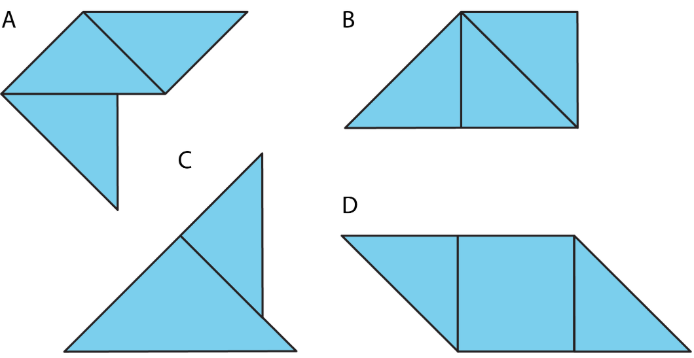
- Figure A
- Figure B
- Figure C
- Figure D
Exercise 1.2.7
The area of a rectangular playground is 78 square meters. If the length of the playground is 13 meters, what is its width?
(From Unit 1.1.1)
Exercise 1.2.8
A student said, “We can’t find the area of the shaded region because the shape has many different measurements, instead of just a length and a width that we could multiply.”
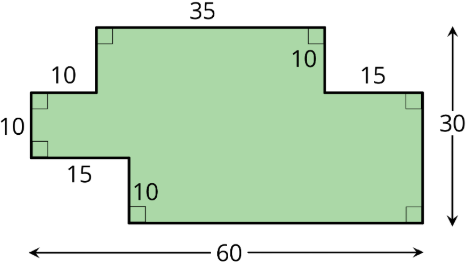
Explain why the student's statement about area is incorrect.
(From Unit 1.1.1)


