1.3: Reasoning to Find Area

Last updated
Save as PDF

Page ID: 39429

Illustrative Mathematics
OpenUp Resources

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Lesson

Let's decompose and rearrange shapes to find their areas.

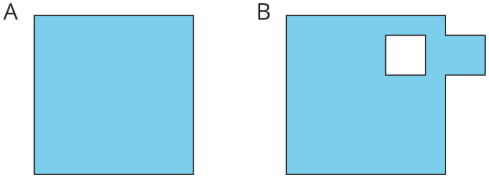
Exercise \(\PageIndex{1}\): Comparing Regions

Is the area of Figure A greater than, less than, or equal to the area of the shaded region in Figure B? Be prepared to explain your reasoning.

Exercise \(\PageIndex{2}\): On the Grid

Each grid square is 1 square unit. Find the area, in square units, of each shaded region without counting every square. Be prepared to explain your reasoning.

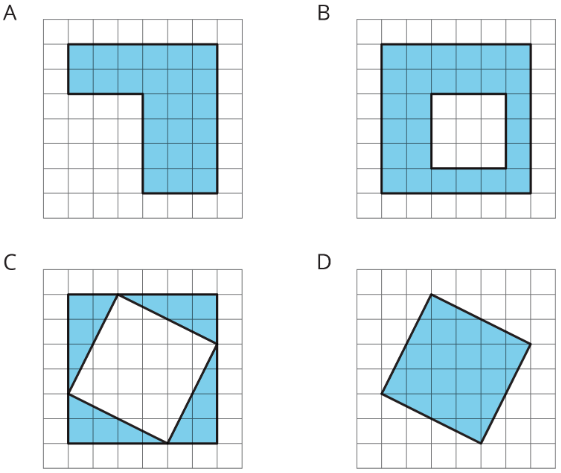
Are you ready for more?

Rearrange the triangles from Figure C so they fit inside Figure D. Draw and color a diagram of your work.

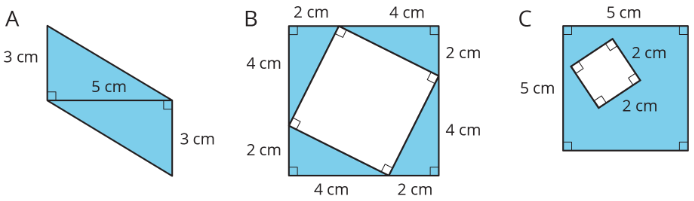
Exercise \(\PageIndex{3}\): Off the Grid

Find the area of the shaded region(s) of each figure. Explain or show your reasoning.

Figure C, square with side length = 5 centimeters. tilted white square with side length = 2 centimeters inside of square. Area around the white square is shaded.

Summary

There are different strategies we can use to find the area of a region. We can:

Decompose it into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.

Figure \(\PageIndex{4}\): Two images of t-shaped objects on a grids. The upper portion is 2 units tall and 6 units wide. The stem of the t is 4 units tall and 2 units wide. The second image is the same, except there is a line separating the upper portion and lower portion into two rectangles.

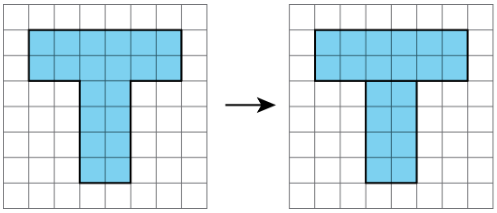
Decompose it and rearrange the pieces into shapes whose areas you know how to calculate; find the area of each of those shapes, and then add the areas.

Figure \(\PageIndex{5}\): 3 figures on grids with arrows pointing to the right between figures 1 and 2 and figures 2 and 3. On the left is an irregular figure. In the middle, the figure has been divided into two triangles with base = 3 units, height = 4 units. the triangle on the right has been moved 3 units left and 2 units down. On the right, rectangle made up of the two triangles from the figures on the left and in the middle. base = 3 units, height = 4 units.

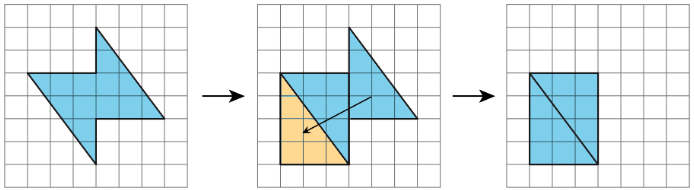
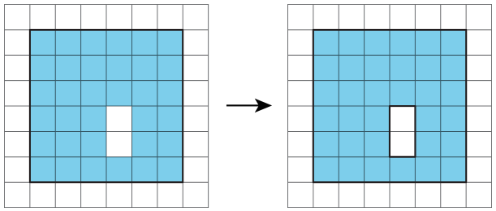
Consider it as a shape with a missing piece; calculate the area of the shape and the missing piece, and then subtract the area of the piece from the area of the shape.

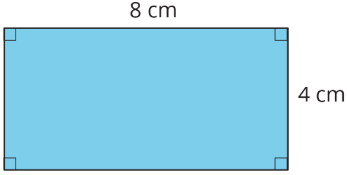
The area of a figure is always measured in square units. When both side lengths of a rectangle are given in centimeters, then the area is given in square centimeters. For example, the area of this rectangle is 32 square centimeters.

Glossary Entries

Definition: Area

Area is the number of square units that cover a two-dimensional region, without any gaps or overlaps.

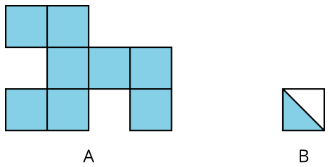
For example, the area of region A is 8 square units. The area of the shaded region of B is \(\frac{1}{2}\) square unit.

Definition: Compose

Compose means “put together.” We use the word compose to describe putting more than one figure together to make a new shape.

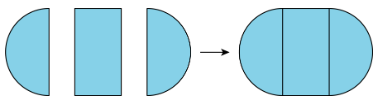
Definition: Decompose

Decompose means “take apart.” We use the word decompose to describe taking a figure apart to make more than one new shape.

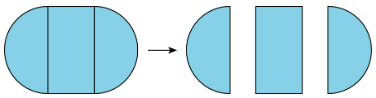
Definition: Region

A region is the space inside of a shape. Some examples of two-dimensional regions are inside a circle or inside a polygon. Some examples of three-dimensional regions are the inside of a cube or the inside of a sphere.

Practice

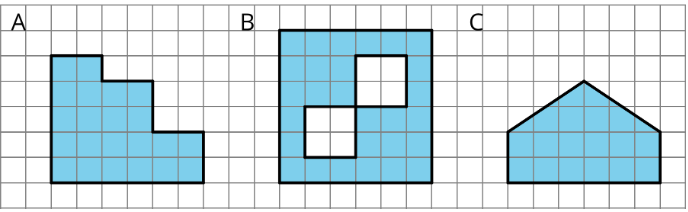
Exercise \(\PageIndex{4}\)

Find the area of each shaded region. Show your reasoning.

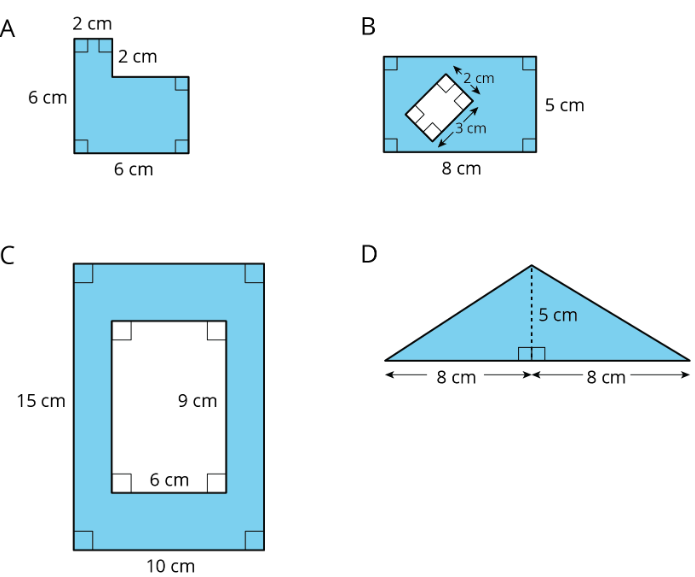
Exercise \(\PageIndex{5}\)

Find the area of each shaded region. Show or explain your reasoning.

Figure D, triangle, base = 16 centimeters, height = 5 centimeters. Triangle is symmetric.

Exercise \(\PageIndex{6}\)

Two plots of land have very different shapes. Noah said that both plots of land have the same area.

Figure \(\PageIndex{13}\): Two shapes labeled plot A and plot B. Plot A is a rectangle and plot B is the same height, but has a triangular shape removed from the right side, and an identical triangle shape added to the left side.

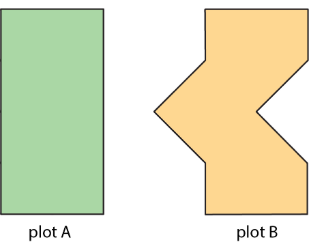
Do you agree with Noah? Explain your reasoning.

Exercise \(\PageIndex{7}\)

A homeowner is deciding on the size of tiles to use to fully tile a rectangular wall in her bathroom that is 80 inches by 40 inches. The tiles are squares and come in three side lengths: 8 inches, 4 inches, and 2 inches. State if you agree with each statement about the tiles. Explain your reasoning.

Regardless of the size she chooses, she will need the same number of tiles.
Regardless of the size she chooses, the area of the wall that is being tiled is the same.
She will need two 2-inch tiles to cover the same area as one 4-inch tile.
She will need four 4-inch tiles to cover the same area as one 8-inch tile.
If she chooses the 8-inch tiles, she will need a quarter as many tiles as she would with 2-inch tiles.

(From Unit 1.1.2)