18.1: Percentages and Double Number Lines

Last updated

Mar 27, 2022
Save as PDF
- Section 18: Percentages
- 18.2: Percentages and Tape Diagrams

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

Lesson

Let's use double number lines to represent percentages.

Exercise $\PageIndex{1}$ : Fundraising Goal

Each of three friends—Lin, Jada, and Andre—had the goal of raising $40. How much money did each person raise? Be prepared to explain your reasoning.

Lin raised 100% of her goal.
Jada raised 50% of her goal.
Andre raised 150% of his goal.

Exercise $\PageIndex{2}$ : Three-Day Biking Trip

Elena biked 8 miles on Saturday. Use the double number line to answer the questions. Be prepared to explain your reasoning.

Figure $\PageIndex{1}$ : A double number line for distance in miles with 7 evenly spaced tick marks. The top number line has the number 0 on the first tick mark and the remaining tick marks are blank. The bottom number line starting with the first tick mark, 0 percent, 25 percent, 50 percent, 75 percent, 100 percent, 125 percent and 150 percent are labeled.

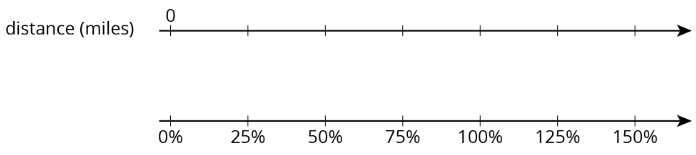
What is 100% of her Saturday distance?
On Sunday, she biked 75% of her Saturday distance. How far was that?
On Monday, she biked 125% of her Saturday distance. How far was that?

Exercise $\PageIndex{3}$ : Puppies Grow Up

Jada has a new puppy that weighs 9 pounds. The vet says that the puppy is now at about 20% of its adult weight. What will be the adult weight of the puppy?

Andre also has a puppy that weighs 9 pounds. The vet says that this puppy is now at about 30% of its adult weight. What will be the adult weight of Andre’s puppy?

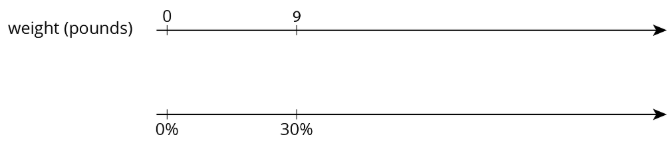
What is the same about Jada and Andre’s puppies? What is different?

Are you ready for more?

A loaf of bread costs $2.50 today. The same size loaf cost 20 cents in 1955.

What percentage of today’s price did someone in 1955 pay for bread?
A job pays $10.00 an hour today. If the same percentage applies to income as well, how much would that job have paid in 1955?

Summary

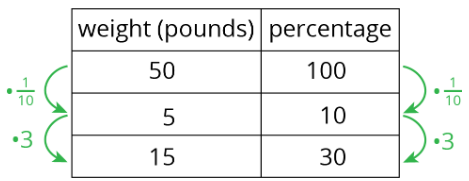
We can use a double number line to solve problems about percentages. For example, what is 30% of 50 pounds? We can draw a double number line like this:

We divide the distance between 0% and 100% and that between 0 and 50 pounds into ten equal parts. We label the tick marks on the top line by counting by 5s ( $50\div 10=5$ ) and on the bottom line counting by 10% ( $100\div 10=10$ ). We can then see that 30% of 50 pounds is 15 pounds.

We can also use a table to solve this problem.

Figure $\PageIndex{5}$ : A 2-column table with 3 rows of data. First column, weight, pounds. Data are as follows: 50, 5, 15. Second column, percentage. Data are as follows: 100, 10, 30. Arrow between first and second row says times the fraction 1 over 10. Arrow between second and third row says times 3.

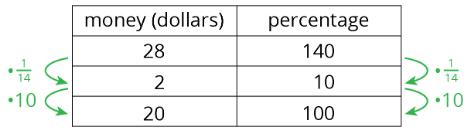
Suppose we know that 140% of an amount is $28. What is 100% of that amount? Let’s use a double number line to find out.

Figure $\PageIndex{6}$ : A double number line with 17 evenly spaced tick marks. The top number line is labeled money, in dollars and the first tick mark is labeled 0, the eleventh tick mark is labeled with a question mark, and the fifteenth tick mark is labeled 28. The bottom number line is unlabeled and the first tick mark is labeled 0 percent, the eleventh tick mark is labeled 100 percent, and the fifteenth tick mark is labeled 140 percent.

We divide the distance between 0% and 140% and that between $0 and $28 into fourteen equal intervals. We label the tick marks on the top line by counting by 2s and on the bottom line counting by 10%. We would then see that 100% is $20.

Or we can use a table as shown.

Figure $\PageIndex{7}$ : A two column table with three rows of data. The first column has the heading weight, in pounds. The second column has the heading percentage. Row 1; 28, 140. Row 2; 2, 10. Row 3; 20, 100. Arrows on both sides of the table from row 1 to row 2 are labeled multiply by one fourteenth. Arrows on both sides of the table from row 2 to row 3 are labeled multiply by 10.

Glossary Entries

Definition: Percent

The word percent means “for each 100.” The symbol for percent is %.

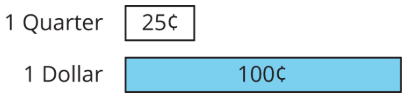
For example, a quarter is worth 25 cents, and a dollar is worth 100 cents. We can say that a quarter is worth 25% of a dollar.

Figure $\PageIndex{9}$ : A diagram of two bars with different lengths. The top bar is labeled 1 Quarter and 25 cents is labeled inside the bar. The bottom bar is labeled 1 Dollar. It is 4 times longer than the top bar and 100 cents is labeled inside the bar.

Definition: Percentage

A percentage is a rate per 100.

For example, a fish tank can hold 36 liters. Right now there is 27 liters of water in the tank. The percentage of the tank that is full is 75%.

Practice

Exercise $\PageIndex{4}$

Solve each problem. If you get stuck, consider using the double number lines.

During a basketball practice, Mai attempted 40 free throws and was successful on 25% of them. How many successful free throws did she make?

Figure $\PageIndex{11}$ : A double number line with 7 evenly spaced tick marks. The top number line is labeled free throws and the first tick mark is labeled 0. The other tick marks are unlabeled. The bottom number line is not labeled and starting with the first tick mark 0, 25 percent, 50 percent, 75 percent, 100 percent, 125 percent, and 150 percent are labeled.

Yesterday, Priya successfully made 12 free throws. Today, she made 150% as many. How many successful free throws did Priya make today?

Figure $\PageIndex{12}$ : A double number line with 7 evenly spaced tick marks. The top number line is labeled free throws and the first tick mark is labeled 0. The other tick marks are unlabeled. The bottom number line is not labeled and starting with the first tick mark 0, 25 percent, 50 percent, 75 percent, 100 percent, 125 percent, and 150 percent are labeled.

Exercise $\PageIndex{5}$

A 16-ounce bottle of orange juice says it contains 200 milligrams of vitamin C, which is 250% of the daily recommended allowance of vitamin C for adults. What is 100% of the daily recommended allowance of vitamin C for adults?

Exercise $\PageIndex{6}$

At a school, 40% of the sixth-grade students said that hip-hop is their favorite kind of music. If 100 sixth-grade students prefer hip hop music, how many sixth-grade students are at the school? Explain or show your reasoning.

Exercise $\PageIndex{7}$

Diego has a skateboard, scooter, bike, and go-cart. He wants to know which vehicle is the fastest. A friend records how far Diego travels on each vehicle in 5 seconds. For each vehicle, Diego travels as fast as he can along a straight, level path.

Table $\PageIndex{1}$
vehicle	distance traveled
skateboard	$90$ feet
scooter	$1,020$ inches
bike	$4,800$ centimeters
go-cart	$0.03$ kilometers

What is the distance each vehicle traveled in centimeters?
Rank the vehicles in order from fastest to slowest.

(From Unit 3.3.5)

Exercise $\PageIndex{8}$

It takes 10 pounds of potatoes to make 15 pounds of mashed potatoes. At this rate:

How many pounds of mashed potatoes can they make with 15 pounds of potatoes?
How many pounds of potatoes are needed to make 50 pounds of mashed potatoes?

(From Unit 3.3.3)

Search

Text Color

Text Size

Margin Size

Font Type

Lesson

Summary

Glossary Entries

Practice

Support Center

How can we help?