5.3: Decimal Operations (Part 1)
- Page ID
- 4999
- Add and subtract decimals
- Multiply decimals
- Divide decimals
- Use decimals in money applications
Before you get started, take this readiness quiz.
- Simplify \(\dfrac{70}{100}\). If you missed this problem, review Example 4.3.1.
- Multiply \(\dfrac{3}{10} \cdot \dfrac{9}{10}\). If you missed this problem, review Example 4.3.7.
- Divide −36 ÷ (−9). If you missed this problem, review Example 3.7.3.
Add and Subtract Decimals
Let’s take one more look at the lunch order from the start of Decimals, this time noticing how the numbers were added together.
\[\begin{split} & $3.45 \quad Sandwich \\ & $1.25 \quad Water \\ + & $0.33 \quad Tax \\ \hline & $5.03 \quad Total \end{split}\]
All three items (sandwich, water, tax) were priced in dollars and cents, so we lined up the dollars under the dollars and the cents under the cents, with the decimal points lined up between them. Then we just added each column, as if we were adding whole numbers. By lining up decimals this way, we can add or subtract the corresponding place values just as we did with whole numbers.
Step 1. Write the numbers vertically so the decimal points line up.
Step 2. Use zeros as place holders, as needed.
Step 3. Add or subtract the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers.
Add: 3.7 + 12.4.
Solution
| Write the numbers vertically so the decimal points line up. | $$\begin{split} 3.&7 \\ + 12.&4 \\ \hline \end{split}$$ |
| Place holders are not needed since both numbers have the same number of decimal places. | |
| Add the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers. | $$\begin{split} \stackrel{1}{3}.&7 \\ + 12.&4 \\ \hline 16.&1 \end{split}$$ |
Add: 5.7 + 11.9.
- Answer
-
\(17.6\)
Add: 18.32 + 14.79.
- Answer
-
\(13.11\)
Add: 23.5 + 41.38.
Solution
| Write the numbers vertically so the decimal points line up. | $$\begin{split} 23.&5 \\ + 41.&38 \\ \hline \end{split}$$ |
| Place 0 as a place holder after the 5 in 23.5, so that both numbers have two decimal places. | $$\begin{split} 23.&5 \textcolor{red}{0} \\ + 41.&38 \\ \hline \end{split}$$ |
| Add the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers. | $$\begin{split} 23.&50 \\ + 41.&38 \\ \hline 64.&88 \end{split}$$ |
Add: 4.8 + 11.69.
- Answer
-
\(16.49\)
Add: 5.123 + 18.47.
- Answer
-
\(23.593\)
How much change would you get if you handed the cashier a $20 bill for a $14.65 purchase? We will show the steps to calculate this in the next example.
Subtract: 20 − 14.65.
Solution
| Write the numbers vertically so the decimal points line up. Remember 20 is a whole number, so place the decimal point after the 0. | $$\begin{split} 20.& \\ - 14.&65 \\ \hline \end{split}$$ |
| Place two zeros after the decimal point in 20, as place holders so that both numbers have two decimal places. |
\[\begin{split} 20.& \textcolor{red}{00} \\ - 14.&65 \\ \hline \end{split}\] |
| Subtract the numbers as if they were whole numbers. Then place the decimal in the answer under the decimal points in the given numbers. | $$\begin{split} \stackrel{1}{\cancel{2}} \stackrel{\stackrel{9}{\cancel{10}}}{\cancel{0}} &.\stackrel{\stackrel{9}{\cancel{10}}}{\cancel{0}} \stackrel{\stackrel{9}{\cancel{10}}}{\cancel{0}} \\ - 1\; \; 4\; \; &.\; 6\; \; 5 \\ \hline 5\; \; &.\; 3\; \; 5\end{split}$$ |
Subtract: 10 − 9.58.
- Answer
-
\(0.42\)
Subtract: 50 − 37.42.
- Answer
-
\(12.58\)
Subtract: 2.51 − 7.4.
Solution
If we subtract 7.4 from 2.51, the answer will be negative since 7.4 > 2.51. To subtract easily, we can subtract 2.51 from 7.4. Then we will place the negative sign in the result.
| Write the numbers vertically so the decimal points line up. | $$\begin{split} 7.&4 \\ - 2.&51 \\ \hline \end{split}$$ |
| Place zero after the 4 in 7.4 as a place holder, so that both numbers have two decimal places. | $$\begin{split} 7.&4 \textcolor{red}{0} \\ - 2.&51 \\ \hline \end{split}$$ |
| Subtract and place the decimal in the answer. | $$\begin{split} 7.&40 \\ - 2.&51 \\ \hline 4.&89 \end{split}$$ |
| Remember that we are really subtracting 2.51 − 7.4 so the answer is negative. | 2.51 − 7.4 = − 4.89 |
Subtract: 4.77 − 6.3.
- Answer
-
\(-1.53\)
Subtract: 8.12 − 11.7.
- Answer
-
\(-3.58\)
Multiply Decimals
Multiplying decimals is very much like multiplying whole numbers—we just have to determine where to place the decimal point. The procedure for multiplying decimals will make sense if we first review multiplying fractions.
Do you remember how to multiply fractions? To multiply fractions, you multiply the numerators and then multiply the denominators. So let’s see what we would get as the product of decimals by converting them to fractions first. We will do two examples side-by-side in Table 5.22. Look for a pattern.
| A | B | |
|---|---|---|
| (0.3)(0.7) | (0.2)(0.46) | |
| Convert to fractions. | $$\left(\dfrac{3}{10}\right) \left(\dfrac{7}{10}\right)$$ | $$\left(\dfrac{2}{10}\right) \left(\dfrac{46}{100}\right)$$ |
| Multiply. | $$\dfrac{21}{100}$$ | $$\dfrac{92}{1000}$$ |
| Convert back to decimals | 0.21 | 0.092 |
There is a pattern that we can use. In A, we multiplied two numbers that each had one decimal place, and the product had two decimal places. In B, we multiplied a number with one decimal place by a number with two decimal places, and the product had three decimal places.
How many decimal places would you expect for the product of (0.01)(0.004)? If you said “five”, you recognized the pattern. When we multiply two numbers with decimals, we count all the decimal places in the factors—in this case two plus three—to get the number of decimal places in the product—in this case five.
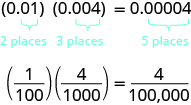
Once we know how to determine the number of digits after the decimal point, we can multiply decimal numbers without converting them to fractions first. The number of decimal places in the product is the sum of the number of decimal places in the factors.
The rules for multiplying positive and negative numbers apply to decimals, too, of course.
When multiplying two numbers,
- if their signs are the same, the product is positive.
- if their signs are different, the product is negative.
When you multiply signed decimals, first determine the sign of the product and then multiply as if the numbers were both positive. Finally, write the product with the appropriate sign.
Step 1. Determine the sign of the product.
Step 2. Write the numbers in vertical format, lining up the numbers on the right.
Step 3. Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points.
Step 4. Place the decimal point. The number of decimal places in the product is the sum of the number of decimal places in the factors. If needed, use zeros as placeholders.
Step 5. Write the product with the appropriate sign.
Multiply: (3.9)(4.075).
Solution
| Determine the sign of the product. The signs are the same. | The product will be positive. |
| Write the numbers in vertical format, lining up the numbers on the right. | $$\begin{split} 4.07&5 \\ \times 3.&9 \\ \hline \end{split}$$ |
| Multiply the numbers as if they were whole numbers, temporarily ignoring the decimal points. | $$\begin{split} 4.07&5 \\ \times 3.&9 \\ \hline 3667&5 \\ 12225&\; \\ \hline 15892&5 \end{split}$$ |
| Place the decimal point. Add the number of decimal places in the factors (1 + 3). Place the decimal point 4 places from the right. | $$\begin{split} 4.07&5 \quad \textcolor{blue}{3\; places} \\ \times 3.&9 \quad \textcolor{blue}{1\; place}\\ \hline 3667&5 \\ 12225&\; \\ \hline 15892&5 \quad \textcolor{blue}{4\; places} \end{split}$$ |
| The product is positive. | (3.9)(4.075) = 15.8925 |
Multiply: 4.5(6.107).
- Answer
-
\(27.4815\)
Multiply: 10.79(8.12).
- Answer
-
\(87.6148\)
Multiply: (−8.2)(5.19).
Solution
| The signs are different. | The product will be negative. |
| Write in vertical format, lining up the numbers on the right. | $$\begin{split} 5.&19 \\ \times 8.&2 \\ \hline \end{split}$$ |
| Multiply. | $$\begin{split} 5.&19 \\ \times 8.&2 \\ \hline 10&38 \\ 415&2\; \\ \hline 425&58 \end{split}$$ |
 |
$$\begin{split} 5.&19 \\ \times 8.&2 \\ \hline 10&38 \\ 415&2\; \\ \hline 42.5&58 \end{split}$$ |
| The product is negative. | (−8.2)(5.19) = −42.558 |
Multiply: (4.63)(−2.9).
- Answer
-
\(-13.427\)
Multiply: (−7.78)(4.9).
- Answer
-
\(-38.122\)
In the next example, we’ll need to add several placeholder zeros to properly place the decimal point.
Multiply: (0.03)(0.045).
Solution
| The product is positive. | (0.03)(0.045) |
| Write in vertical format, lining up the numbers on the right. | $$\begin{split} 0.04&5 \\ \times 0.0&3 \\ \hline \end{split}$$ |
| Multiply. | $$\begin{split} 0.04&5 \\ \times 0.0&3 \\ \hline 13&5 \end{split}$$ |
|
Add zeros as needed to get the 5 places. |
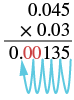 |
| The product is positive. | (0.03)(0.045) = 0.00135 |
Multiply: (0.04)(0.087).
- Answer
-
\(0.00348\)
Multiply: (0.09)(0.067).
- Answer
-
\(0.00603\)
Multiply by Powers of 10
In many fields, especially in the sciences, it is common to multiply decimals by powers of 10. Let’s see what happens when we multiply 1.9436 by some powers of 10.
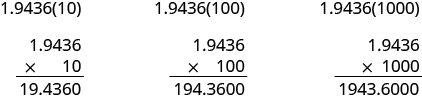
Look at the results without the final zeros. Do you notice a pattern?
\[\begin{split} 1.9436(10) & = 19.436 \\ 1.9436(100) & = 194.36 \\ 1.9436(1000) & = 1943.6 \end{split}\]
The number of places that the decimal point moved is the same as the number of zeros in the power of ten. Table 5.26 summarizes the results.
| Multiply by | Number of zeros | Number of places decimal point moves |
|---|---|---|
| 10 | 1 | 1 place to the right |
| 100 | 2 | 2 places to the right |
| 1,000 | 3 | 3 places to the right |
| 10,000 | 4 | 4 places to the right |
We can use this pattern as a shortcut to multiply by powers of ten instead of multiplying using the vertical format. We can count the zeros in the power of 10 and then move the decimal point that same of places to the right. So, for example, to multiply 45.86 by 100, move the decimal point 2 places to the right.
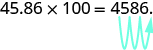
Sometimes when we need to move the decimal point, there are not enough decimal places. In that case, we use zeros as placeholders. For example, let’s multiply 2.4 by 100. We need to move the decimal point 2 places to the right. Since there is only one digit to the right of the decimal point, we must write a 0 in the hundredths place.
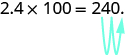
Step 1. Move the decimal point to the right the same number of places as the number of zeros in the power of 10.
Step 2. Write zeros at the end of the number as placeholders if needed.
Multiply 5.63 by factors of (a) 10 (b) 100 (c) 1000.
Solution
By looking at the number of zeros in the multiple of ten, we see the number of places we need to move the decimal to the right.
(a) 5.63(10)
| There is 1 zero in 10, so move the decimal point 1 place to the right. | 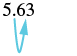 |
| 56.3 |
(b) 5.63(100)
| There are 2 zeros in 100, so move the decimal point 2 places to the right. | 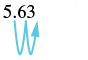 |
| 563 |
(c) 5.63(1000)
| There are 3 zeros in 1000, so move the decimal point 3 places to the right. | 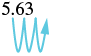 |
| A zero must be added at the end. | 5,630 |
Multiply 2.58 by factors of (a) 10 (b) 100 (c) 1000.
- Answer a
-
\(25.8\)
- Answer b
-
\(258\)
- Answer c
-
\(2,580\)
Multiply 14.2 by factors of (a) 10 (b) 100 (c) 1000.
- Answer a
-
\(142\)
- Answer b
-
\(1,420\)
- Answer c
-
\(14,200\)
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."



