5.2: Decimals (Part 2)
- Page ID
- 6221
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Locate Decimals on the Number Line
Since decimals are forms of fractions, locating decimals on the number line is similar to locating fractions on the number line.
Locate 0.4 on a number line.
Solution
The decimal 0.4 is equivalent to \(\dfrac{4}{10}\), so 0.4 is located between 0 and 1. On a number line, divide the interval between 0 and 1 into 10 equal parts and place marks to separate the parts.
Label the marks 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. We write 0 as 0.0 and 1 as 1.0, so that the numbers are consistently in tenths. Finally, mark 0.4 on the number line.

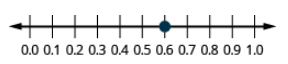
Locate 0.6 on a number line.
- Answer
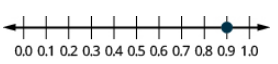
Locate 0.9 on a number line.
- Answer
-
Locate −0.74 on a number line.
Solution
The decimal −0.74 is equivalent to \(− \dfrac{74}{100}\), so it is located between 0 and −1. On a number line, mark off and label the multiples of -0.10 in the interval between 0 and −1 (−0.10, −0.20, etc.) and mark −0.74 between −0.70 and −0.80, a little closer to −0.70.
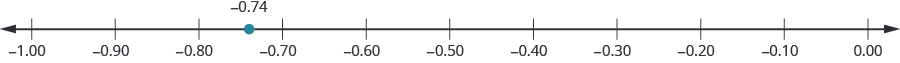
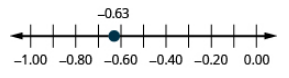
Locate −0.63 on a number line.
- Answer
Locate −0.25 on a number line.
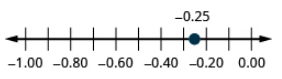
- Answer
Order Decimals
Which is larger, 0.04 or 0.40?
If you think of this as money, you know that $0.40 (forty cents) is greater than $0.04 (four cents). So, 0.40 > 0.04.
In previous chapters, we used the number line to order numbers.
a < b: ‘a is less than b’ when a is to the left of b on the number line
a > b: ‘a is greater than b’ when a is to the right of b on the number line
Where are 0.04 and 0.40 located on the number line?

We see that 0.40 is to the right of 0.04. So we know 0.40 > 0.04.
How does 0.31 compare to 0.308? This doesn’t translate into money to make the comparison easy. But if we convert 0.31 and 0.308 to fractions, we can tell which is larger.
| 0.31 | 0.308 | |
| Convert to fractions. | $$\dfrac{31}{100}$$ | $$\dfrac{308}{1000}$$ |
| We need a common denominator to compare them. | $$\dfrac{31 \cdot \textcolor{red}{10}}{100 \cdot \textcolor{red}{10}}$$ | $$\dfrac{308}{1000}$$ |
| $$\dfrac{310}{1000}$$ | $$\dfrac{308}{1000}$$ |
Because 310 > 308, we know that \(\dfrac{310}{1000} > \dfrac{308}{1000}\). Therefore, 0.31 > 0.308.
Notice what we did in converting 0.31 to a fraction—we started with the fraction \(\dfrac{31}{100}\) and ended with the equivalent fraction \(\dfrac{310}{1000}\). Converting \(\dfrac{310}{1000}\) back to a decimal gives 0.310. So 0.31 is equivalent to 0.310. Writing zeros at the end of a decimal does not change its value.
\[\dfrac{31}{100} = \dfrac{310}{1000} \quad and \quad 0.31 = 0.310\]
If two decimals have the same value, they are said to be equivalent decimals.
\[0.31 = 0.310\]
We say 0.31 and 0.310 are equivalent decimals.
Step 1. Check to see if both numbers have the same number of decimal places. If not, write zeros at the end of the one with fewer digits to make them match.
Step 2. Compare the numbers to the right of the decimal point as if they were whole numbers.
Step 3. Order the numbers using the appropriate inequality sign.
Order the following decimals using < or >: (a) 0.64 __0.6 (b) 0.83 __0.803
Solution
(a) 0.64 __0.6
| Check to see if both numbers have the same number of decimal places. They do not, so write one zero at the right of 0.6. | 0.64 __0.60 |
| Compare the numbers to the right of the decimal point as if they were whole numbers. | 64 > 60 |
| Order the numbers using the appropriate inequality sign. |
0.64 > 0.60 0.64 > 0.6 |
(b) 0.83 __0.803
| Check to see if both numbers have the same number of decimal places. They do not, so write one zero at the right of 0.83. | 0.830 __0.803 |
| Compare the numbers to the right of the decimal point as if they were whole numbers. | 830 > 803 |
| Order the numbers using the appropriate inequality sign. |
0.830 > 0.803 0.83 > 0.803 |
Order each of the following pairs of numbers, using < or >: (a) 0.42__0.4 (b) 0.76__0.706
- Answer a
-
>
- Answer b
-
>
Order each of the following pairs of numbers, using < or >: (a) 0.1__0.18 (b) 0.305__0.35
- Answer a
-
<
- Answer b
-
<
When we order negative decimals, it is important to remember how to order negative integers. Recall that larger numbers are to the right on the number line. For example, because −2 lies to the right of −3 on the number line, we know that −2 > −3. Similarly, smaller numbers lie to the left on the number line. For example, because −9 lies to the left of −6 on the number line, we know that −9 < −6.
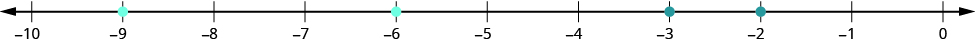
If we zoomed in on the interval between 0 and −1, we would see in the same way that −0.2 > −0.3 and −0.9 < −0.6.
Use < or > to order. −0.1__−0.8.
Solution
| Write the numbers one under the other, lining up the decimal points. |
−0.1 −0.8 |
| They have the same number of digits. | |
| Since −1 > −8, −1 tenth is greater than −8 tenths. | −0.1 > −0.8 |
Order each of the following pairs of numbers, using < or >: −0.3___−0.5
- Answer
-
>
Order each of the following pairs of numbers, using < or >: −0.6___−0.7
- Answer
-
>
Round Decimals
In the United States, gasoline prices are usually written with the decimal part as thousandths of a dollar. For example, a gas station might post the price of unleaded gas at $3.279 per gallon. But if you were to buy exactly one gallon of gas at this price, you would pay $3.28 , because the final price would be rounded to the nearest cent. In Whole Numbers, we saw that we round numbers to get an approximate value when the exact value is not needed. Suppose we wanted to round $2.72 to the nearest dollar. Is it closer to $2 or to $3? What if we wanted to round $2.72 to the nearest ten cents; is it closer to $2.70 or to $2.80? The number lines in Figure \(\PageIndex{3}\) can help us answer those questions.

Figure \(\PageIndex{3}\) - (b) We see that 2.72 is closer to 3 than to 2. So, 2.72 rounded to the nearest whole number is 3. (b) We see that 2.72 is closer to 2.70 than 2.80. So we say that 2.72 rounded to the nearest tenth is 2.7.
Can we round decimals without number lines? Yes! We use a method based on the one we used to round whole numbers.
Step 1. Locate the given place value and mark it with an arrow.
Step 2. Underline the digit to the right of the given place value.
Step 3. Is this digit greater than or equal to 5?
- Yes - add 1 to the digit in the given place value.
- No - do not change the digit in the given place value
Step 4. Rewrite the number, removing all digits to the right of the given place value.
Round 18.379 to the nearest hundredth.
Solution
| Locate the hundredths place and mark it with an arrow. |  |
| Underline the digit to the right of the 7. | 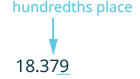 |
| Because 9 is greater than or equal to 5, add 1 to the 7. |  |
| Rewrite the number, deleting all digits to the right of the hundredths place. | 18.38 |
18.38 is 18.379 rounded to the nearest hundredth.
Round to the nearest hundredth: 1.047.
- Answer
-
1.05
Round to the nearest hundredth: 9.173.
- Answer
-
9.17
Round 18.379 to the nearest (a) tenth (b) whole number.
Solution
(a) Round 18.379 to the nearest tenth.
| Locate the tenths place and mark it with an arrow. |  |
| Underline the digit to the right of the tenths digit. |  |
| Because 7 is greater than or equal to 5, add 1 to the 3. |  |
| Rewrite the number, deleting all digits to the right of the tenths place. | 18.4 |
So, 18.379 rounded to the nearest tenth is 18.4.
(b) Round 18.379 to the nearest whole number.
| Locate the ones place and mark it with an arrow. | 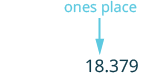 |
| Underline the digit to the right of the ones place. |  |
| Since 3 is not greater than or equal to 5, do not add 1 to the 8. |  |
| Rewrite the number, deleting all digits to the right of the ones place. | 18 |
So 18.379 rounded to the nearest whole number is 18.
Round 6.582 to the nearest (a) hundredth (b) tenth (c) whole number.
- Answer a
-
6.58
- Answer b
-
6.6
- Answer c
-
7
Round 15.2175 to the nearest (a) thousandth (b) hundredth (c) tenth.
- Answer a
-
15.218
- Answer b
-
15.22
- Answer c
-
15.2
Introduction to Decimal Notation
Write a Number in Decimal Notation from Words
Identify Decimals on the Number Line
Rounding Decimals
Writing a Decimal as a Simplified Fraction
Practice Makes Perfect
Name Decimals In the following exercises, name each decimal.
- 5.5
- 7.8
- 5.01
- 14.02
- 8.71
- 2.64
- 0.002
- 0.005
- 0.381
- 0.479
- −17.9
- −31.4
Write Decimals
In the following exercises, translate the name into a decimal number.
- Eight and three hundredths
- Nine and seven hundredths
- Twenty-nine and eighty-one hundredths
- Sixty-one and seventy-four hundredths
- Seven tenths
- Six tenths
- One thousandth
- Nine thousandths
- Twenty-nine thousandths
- Thirty-five thousandths
- Negative eleven and nine ten-thousandths
- Negative fifty-nine and two ten-thousandths
- Thirteen and three hundred ninety-five ten thousandths
- Thirty and two hundred seventy-nine thousandths
Convert Decimals to Fractions or Mixed Numbers
In the following exercises, convert each decimal to a fraction or mixed number.
- 1.99
- 5.83
- 15.7
- 18.1
- 0.239
- 0.373
- 0.13
- 0.19
- 0.011
- 0.049
- −0.00007
- −0.00003
- 6.4
- 5.2
- 7.05
- 9.04
- 4.006
- 2.008
- 10.25
- 12.75
- 1.324
- 2.482
- 14.125
- 20.375
Locate Decimals on the Number Line
In the following exercises, locate each number on a number line.
- 0.8
- 0.3
- −0.2
- −0.9
- 3.1
- 2.7
- −2.5
- −1.6
Order Decimals
In the following exercises, order each of the following pairs of numbers, using < or >.
- 0.9__0.6
- 0.7__0.8
- 0.37__0.63
- 0.86__0.69
- 0.6__0.59
- 0.27__0.3
- 0.91__0.901
- 0.415__0.41
- −0.5__−0.3
- −0.1_−0.4
- −0.62_−0.619
- −7.31_−7.3
Round Decimals
In the following exercises, round each number to the nearest tenth.
- 0.67
- 0.49
- 2.84
- 4.63
In the following exercises, round each number to the nearest hundredth.
- 0.845
- 0.761
- 5.7932
- 3.6284
- 0.299
- 0.697
- 4.098
- 7.096
In the following exercises, round each number to the nearest (a) hundredth (b) tenth (c) whole number.
- 5.781
- 1.638
- 63.479
- 84.281
Everyday Math
- Salary Increase Danny got a raise and now makes $58,965.95 a year. Round this number to the nearest: (a) dollar (b) thousand dollars (c) ten thousand dollars.
- New Car Purchase Selena’s new car cost $23,795.95. Round this number to the nearest: (a) dollar (b) thousand dollars (c) ten thousand dollars.
- Sales Tax Hyo Jin lives in San Diego. She bought a refrigerator for $1624.99 and when the clerk calculated the sales tax it came out to exactly $142.186625. Round the sales tax to the nearest (a) penny (b) dollar.
- Sales Tax Jennifer bought a $1,038.99 dining room set for her home in Cincinnati. She calculated the sales tax to be exactly $67.53435. Round the sales tax to the nearest (a) penny (b) dollar.
Writing Exercises
- How does your knowledge of money help you learn about decimals?
- Explain how you write “three and nine hundredths” as a decimal.
- Jim ran a 100-meter race in 12.32 seconds. Tim ran the same race in 12.3 seconds. Who had the faster time, Jim or Tim? How do you know?
- Gerry saw a sign advertising postcards marked for sale at “10 for 0.99¢.” What is wrong with the advertised price?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) If most of your checks were:
…confidently. Congratulations! You have achieved the objectives in this section. Reflect on the study skills you used so that you can continue to use them. What did you do to become confident of your ability to do these things? Be specific.
…with some help. This must be addressed quickly because topics you do not master become potholes in your road to success. In math, every topic builds upon previous work. It is important to make sure you have a strong foundation before you move on. Who can you ask for help? Your fellow classmates and instructor are good resources. Is there a place on campus where math tutors are available? Can your study skills be improved?
…no—I don’t get it! This is a warning sign and you must not ignore it. You should get help right away or you will quickly be overwhelmed. See your instructor as soon as you can to discuss your situation. Together you can come up with a plan to get you the help you need.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


