5.8: Averages and Probability (Part 1)
- Page ID
- 5002
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Calculate the mean of a set of numbers
- Find the median of a set of numbers
- Find the mode of a set of numbers
- Apply the basic definition of probability
Before you get started, take this readiness quiz.
- Simplify: \(\dfrac{4 + 9 + 2}{3}\). If you missed this problem, review Example 4.6.12.
- Simplify: 4(8) + 6(3). If you missed this problem, review Example 2.2.8.
- Convert \(\dfrac{5}{2}\) to a decimal. If you missed this problem, review Example 5.5.1.
One application of decimals that arises often is finding the average of a set of numbers. What do you think of when you hear the word average? Is it your grade point average, the average rent for an apartment in your city, the batting average of a player on your favorite baseball team? The average is a typical value in a set of numerical data. Calculating an average sometimes involves working with decimal numbers. In this section, we will look at three different ways to calculate an average.
Calculate the Mean of a Set of Numbers
The mean is often called the arithmetic average. It is computed by dividing the sum of the values by the number of values. Students want to know the mean of their test scores. Climatologists report that the mean temperature has, or has not, changed. City planners are interested in the mean household size.
Suppose Ethan’s first three test scores were 85, 88, and 94. To find the mean score, he would add them and divide by 3.
\[\dfrac{85 + 88 + 94}{3}\]
\[\dfrac{267}{3}\]
\[89\]
His mean test score is 89 points.
The mean of a set of n numbers is the arithmetic average of the numbers.
\[mean = \dfrac{sum\; of\; values\; in\; data\; set}{n}\]
Step 1. Write the formula for the mean\[mean = \dfrac{sum\; of\; values\; in\; data\; set}{n}\]
Step 2. Find the sum of all the values in the set. Write the sum in the numerator.
Step 3. Count the number, n, of values in the set. Write this number in the denominator.
Step 4. Simplify the fraction.
Step 5. Check to see that the mean is reasonable. It should be greater than the least number and less than the greatest number in the set.
Find the mean of the numbers 8, 12, 15, 9, and 6.
Solution
| Write the formula for the mean. | $$mean = \dfrac{sum\; of\; values\; in\; data\; set}{n}$$ |
| Write the sum of the numbers in the numerator. | $$mean = \dfrac{8 + 12 + 15 + 9 + 6}{n}$$ |
| Count how many numbers are in the set. There are 5 numbers in the set, so n = 5. | $$mean = \dfrac{8 + 12 + 15 + 9 + 6}{5}$$ |
| Add the numbers in the numerator. | $$mean = \dfrac{50}{5}$$ |
| Then divide. | mean = 10 |
| Check to see that the mean is 'typical': 10 is neither less than 6 nor greater than 15. | The mean is 10. |
Find the mean of the numbers: 8, 9, 7, 12, 10, 5.
- Answer
-
\(8.5\)
Find the mean of the numbers: 9, 13, 11, 7, 5.
- Answer
-
\(9\)
The ages of the members of a family who got together for a birthday celebration were 16, 26, 53, 56, 65, 70, 93, and 97 years. Find the mean age.
Solution
| Write the formula for the mean. | $$mean = \dfrac{sum\; of\; values\; in\; data\; set}{n}$$ |
| Write the sum of the numbers in the numerator. | $$mean = \dfrac{16 + 26 + 53 + 56 + 65 + 70 + 93 + 97}{n}$$ |
| Count how many numbers are in the set. Call this n and write it in the denominator. | $$mean = \dfrac{16 + 26 + 53 + 56 + 65 + 70 + 93 + 97}{8}$$ |
| Simplify the fraction. | $$mean = \dfrac{476}{5}$$ |
| mean = 59.5 |
Is 59.5 ‘typical’? Y es, it is neither less than 16 nor greater than 97. The mean age is 59.5 years.
The ages of the four students in Ben’s carpool are 25, 18, 21, and 22. Find the mean age of the students.
- Answer
-
21.5 years
Yen counted the number of emails she received last week. The numbers were 4, 9, 15, 12, 10, 12, and 8. Find the mean number of emails
- Answer
-
10
Did you notice that in the last example, while all the numbers were whole numbers, the mean was 59.5, a number with one decimal place? It is customary to report the mean to one more decimal place than the original numbers. In the next example, all the numbers represent money, and it will make sense to report the mean in dollars and cents.
For the past four months, Daisy’s cell phone bills were $42.75, $50.12, $41.54, $48.15. Find the mean cost of Daisy’s cell phone bills.
Solution
| Write the formula for the mean. | $$mean = \dfrac{sum\; of\; all\; the\; numbers}{n}$$ |
| Write the sum of the numbers in the numerator. | $$mean = \dfrac{sum\; of\; all\; the\; numbers}{4}$$ |
| Count how many numbers are in the set. Call this n and write it in the denominator. | $$mean = \dfrac{42.75 + 50.12 + 41.54 + 48.15}{4}$$ |
| Simplify the fraction. | $$mean = \dfrac{182.56}{4}$$ |
| mean = 45.64 |
Does $45.64 seem ‘typical’ of this set of numbers? Yes, it is neither less than $41.54 nor greater than $50.12. The mean cost of her cell phone bill was $45.64.
Last week Ray recorded how much he spent for lunch each workday. He spent $6.50, $7.25, $4.90, $5.30, and $12.00. Find the mean of how much he spent each day.
- Answer
-
$7.19
Lisa has kept the receipts from the past four trips to the gas station. The receipts show the following amounts: $34.87, $42.31, $38.04, and $43.26. Find the mean.
- Answer
-
$39.62
Find the Median of a Set of Numbers
When Ann, Bianca, Dora, Eve, and Francine sing together on stage, they line up in order of their heights. Their heights, in inches, are shown in Table 5.70.
Table 5.70
| Ann | Bianca | Dora | Eve | Francine |
|---|---|---|---|---|
| 59 | 60 | 65 | 68 | 70 |
Dora is in the middle of the group. Her height, 65″, is the median of the girls’ heights. Half of the heights are less than or equal to Dora’s height, and half are greater than or equal. The median is the middle value.

The median of a set of data values is the middle value.
- Half the data values are less than or equal to the median.
- Half the data values are greater than or equal to the median.
What if Carmen, the pianist, joins the singing group on stage? Carmen is 62 inches tall, so she fits in the height order between Bianca and Dora. Now the data set looks like this:
\[59, 60, 62, 65, 68, 70\]
There is no single middle value. The heights of the six girls can be divided into two equal parts.
\[\underbrace{59, 60, 62} \quad \underbrace{65, 68, 70}\]
Statisticians have agreed that in cases like this the median is the mean of the two values closest to the middle. So the median is the mean of 62 and 65, \(\dfrac{62 + 65}{2}\). The median height is 63.5 inches.
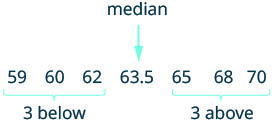
Notice that when the number of girls was 5, the median was the third height, but when the number of girls was 6, the median was the mean of the third and fourth heights. In general, when the number of values is odd, the median will be the one value in the middle, but when the number is even, the median is the mean of the two middle values.
Step 1. List the numbers from smallest to largest.
Step 2. Count how many numbers are in the set. Call this n.
Step 3. Is n odd or even?
- If n is an odd number, the median is the middle value.
- If n is an even number, the median is the mean of the two middle values.
Find the median of 12, 13, 19, 9, 11, 15, and 18.
Solution
| List the numbers in order from smallest to largest. | 9, 11, 12, 13, 15, 18, 19 |
| Count how many numbers are in the set. Call this n. | n = 7 |
| Is n odd or even? | odd |
| The median is the middle value. | 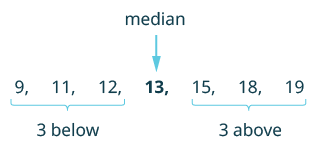 |
| The middle is the number in the 4th position. | So the median of the data is 13. |
Find the median of the data set: 43, 38, 51, 40, 46.
- Answer
-
43
Find the median of the data set: 15, 35, 20, 45, 50, 25, 30.
- Answer
-
30
Kristen received the following scores on her weekly math quizzes: 83, 79, 85, 86, 92, 100, 76, 90, 88, and 64. Find her median score.
Solution
| List the numbers in order from smallest to largest. | 64, 76, 79, 83, 85, 86, 88, 90, 92, 100 |
| Count the number of data values in the set. Call this n. | n = 10 |
| Is n odd or even? | even |
| The median is the mean of the two middle values, the 5th and 6th numbers. |  |
| Find the mean of 85 and 86. | mean = 85.5 |
Kristen's median score is 85.5.
Find the median of the data set: 8, 7, 5, 10, 9, 12.
- Answer
-
8.5
Find the median of the data set: 21, 25, 19, 17, 22, 18, 20, 24.
- Answer
-
20.5
Identify the Mode of a Set of Numbers
The average is one number in a set of numbers that is somehow typical of the whole set of numbers. The mean and median are both often called the average. Yes, it can be confusing when the word average refers to two different numbers, the mean and the median! In fact, there is a third number that is also an average. This average is the mode. The mode of a set of numbers is the number that occurs the most. The frequency, is the number of times a number occurs. So the mode of a set of numbers is the number with the highest frequency.
The mode of a set of numbers is the number with the highest frequency.
Suppose Jolene kept track of the number of miles she ran since the start of the month, as shown in Figure 5.7.
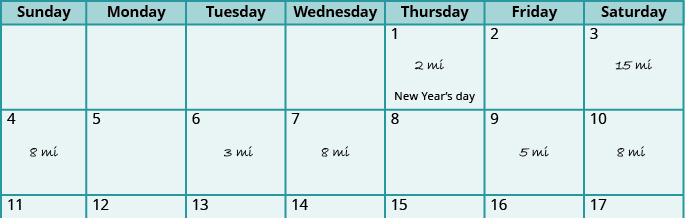
Figure 5.7
If we list the numbers in order it is easier to identify the one with the highest frequency.
\[2, 3, 5, 8, 8, 8, 15\]
Jolene ran 8 miles three times, and every other distance is listed only once. So the mode of the data is 8 miles.
Step 1. List the data values in numerical order.
Step 2. Count the number of times each value appears.
Step 3. The mode is the value with the highest frequency.
The ages of students in a college math class are listed below. Identify the mode.
18, 18, 18, 18, 19, 19, 19, 20, 20, 20, 20, 20, 20, 20, 21, 21, 22, 22, 22, 22, 22, 23, 24, 24, 25, 29, 30, 40, 44
Solution
The ages are already listed in order. We will make a table of frequencies to help identify the age with the highest frequency.

Now look for the highest frequency. The highest frequency is 7, which corresponds to the age 20. So the mode of the ages in this class is 20 years.
The number of sick days employees used last year: 3, 6, 2, 3, 7, 5, 6, 2, 4, 2. Identify the mode.
- Answer
-
2
The number of handbags owned by women in a book club: 5, 6, 3, 1, 5, 8, 1, 5, 8, 5. Identify the mode.
- Answer
-
5
The data lists the heights (in inches) of students in a statistics class. Identify the mode.
| 56 | 61 | 63 | 64 | 65 | 66 | 67 | 67 |
| 60 | 62 | 63 | 64 | 65 | 66 | 67 | 70 |
| 60 | 63 | 63 | 64 | 66 | 66 | 67 | 74 |
| 61 | 63 | 64 | 65 | 66 | 67 | 67 |
Solution
List each number with its frequency.

Now look for the highest frequency. The highest frequency is 6, which corresponds to the height 67 inches. So the mode of this set of heights is 67 inches.
The ages of the students in a statistics class are listed here: 19, 20, 23, 23, 38, 21, 19, 21, 19, 21, 20, 43, 20, 23, 17, 21, 21, 20, 29, 18, 28. What is the mode?
- Answer
-
21
Students listed the number of members in their household as follows: 6, 2, 5, 6, 3, 7, 5, 6, 5, 3, 4, 4, 5, 7, 6, 4, 5, 2, 1, 5. What is the mode?
- Answer
-
5
Some data sets do not have a mode because no value appears more than any other. And some data sets have more than one mode. In a given set, if two or more data values have the same highest frequency, we say they are all modes.
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


