1.1: Introduction to Whole Numbers (Part 1)

Last updated
Save as PDF

Page ID: 4970

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Identify counting numbers and whole numbers
Model whole numbers
Identify the place value of a digit
Use place value to name whole numbers
Use place value to write whole numbers
Round whole numbers

Identify Counting Numbers and Whole Numbers

Learning algebra is similar to learning a language. You start with a basic vocabulary and then add to it as you go along. You need to practice often until the vocabulary becomes easy to you. The more you use the vocabulary, the more familiar it becomes.

Algebra uses numbers and symbols to represent words and ideas. Let’s look at the numbers first. The most basic numbers used in algebra are those we use to count objects: $1, 2, 3, 4, 5, …$ and so on. These are called the counting numbers. The notation “…” is called an ellipsis, which is another way to show “and so on”, or that the pattern continues endlessly. Counting numbers are also called natural numbers.

Definition: Counting Numbers

The counting numbers start with $1$ and continue.

$1, 2, 3, 4, 5 \ldots $

Counting numbers and whole numbers can be visualized on a number line as shown in Figure $\PageIndex{1}$.

$An image of a number line from 0 to 6 in increments of one. An arrow above the number line pointing to the right with the label “larger”. An arrow pointing to the left with the label “smaller”.$

Figure $\PageIndex{1}$: The numbers on the number line increase from left to right, and decrease from right to left.

The point labeled $0$ is called the origin. The points are equally spaced to the right of 0 and labeled with the counting numbers. When a number is paired with a point, it is called the coordinate of the point.

The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called the whole numbers.

Definition: Whole Numbers

The whole numbers are the counting numbers and zero.

$0, 1, 2, 3, 4, 5 \ldots$

We stopped at $5$ when listing the first few counting numbers and whole numbers. We could have written more numbers if they were needed to make the patterns clear.

Example $\PageIndex{1}$: Number Identification

Which of the following are

counting numbers
whole numbers

\[0, \dfrac{1}{4}, 3, 5.2, 15, 105 \nonumber\]

Solution

The counting numbers start at $1$, so $0$ is not a counting number. The numbers $3$, $15$, and $105$ are all counting numbers.
Whole numbers are counting numbers and $0$. The numbers $0, 3, 15,$ and $105$ are whole numbers. The numbers $\dfrac{1}{4}$ and $5.2$ are neither counting numbers nor whole numbers. We will discuss these numbers later.

Exercise $\PageIndex{1}$

Which of the following are

whole numbers

\[0, \dfrac{2}{3}, 2, 9, 11.8, 241, 376 \nonumber \]

Answer a: $2, 9, 241, 376$

Answer b: $0, 2, 9, 241, 376$

Exercise $\PageIndex{2}$

Which of the following are

counting numbers
whole numbers

\[0, \dfrac{5}{3}, 7, 8.8, 13, 201 \nonumber \]

Answer a: $7, 13, 201$

Answer b: $0, 7, 13, 201$

Model Whole Numbers

Our number system is called a place value system because the value of a digit depends on its position, or place, in a number. The number $537$ has a different value than the number $735$. Even though they use the same digits, their value is different because of the different placement of the $3$ and the $7$ and the $5$.

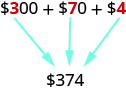
Money gives us a familiar model of place value. Suppose a wallet contains three $$100$ bills, seven $$10$ bills, and four $$1$ bills. The amounts are summarized in Figure $\PageIndex{2}$. How much money is in the wallet?

$An image of three stacks of American currency. First stack from left to right is a stack of 3 $100 bills, with label “Three $100 bills, 3 times $100 equals $300”. Second stack from left to right is a stack of 7 $10 bills, with label “Seven $10 bills, 7 times $10 equals $70”. Third stack from left to right is a stack of 4 $1 bills, with label “Four $1 bills, 4 times $1 equals $4”.$

Figure $\PageIndex{2}$

Find the total value of each kind of bill, and then add to find the total. The wallet contains $$374$.

$An image of “$300 + $70 +$4” where the “3” in “$300”, the “7” in “$70”, and the “4” in “$4” are all in red instead of black like the rest of the expression. Below this expression there is the value “$374”. An arrow points from the red “3” in the expression to the “3” in “$374”, an arrow points to the red “7” in the expression to the “7” in “$374”, and an arrow points from the red “4” in the expression to the “4” in “$374”.$

Base-$10$ blocks provide another way to model place value, as shown in Figure $\PageIndex{3}$. The blocks can be used to represent hundreds, tens, and ones. Notice that the tens rod is made up of $10$ ones, and the hundreds square is made of $10$ tens, or $100$ ones.

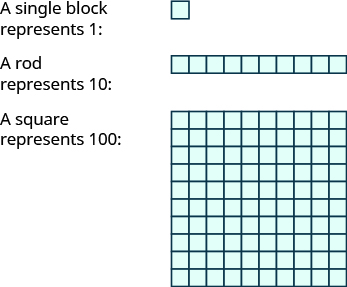
$An image with three items. The first item is a single block with the label “A single block represents 1”. The second item is a horizontal rod consisting of 10 blocks, with the label “A rod represents 10”. The third item is a square consisting of 100 blocks, with the label “A square represents 100”. The square is 10 blocks tall and 10 blocks wide.$

Figure $\PageIndex{3}$

Figure $\PageIndex{4}$ shows the number $138$ modeled with base-$10$ blocks.

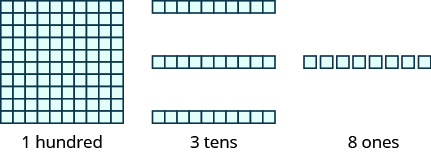
$An image consisting of three items. The first item is a square of 100 blocks, 10 blocks wide and 10 blocks tall, with the label “1 hundred”. The second item is 3 horizontal rods containing 10 blocks each, with the label “3 tens”. The third item is 8 individual blocks with the label “8 ones”.$

Figure $\PageIndex{4}$: We use place value notation to show the value of the number 138.

$An image of “100 + 30 +8” where the “1” in “100”, the “3” in “30”, and the “8” are all in red instead of black like the rest of the expression. Below this expression there is the value “138”. An arrow points from the red “1” in the expression to the “1” in “138”, an arrow points to the red “3” in the expression to the “3” in “138”, and an arrow points from the red “8” in the expression to the “8” in 138.$

Digit	Place value	Number	Value	Total value
1	hundreds	1	100	100
3	tens	3	10	30
8	ones	8	1	+8
			Sum =	138

Example $\PageIndex{2}$: place value notation

Use place value notation to find the value of the number modeled by the base-$10$ blocks shown.

$An image consisting of three items. The first item is two squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is one horizontal rod containing 10 blocks. The third item is 5 individual blocks.$

Figure $\PageIndex{5}$

Solution

There are $2$ hundreds squares, which is $200$.

There is $1$ tens rod, which is $10$.

There are $5$ ones blocks, which is $5$.

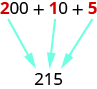
$An image of “200 + 10 + 5” where the “2” in “200”, the “1” in “10”, and the “5” are all in red instead of black like the rest of the expression. Below this expression there is the value “215”. An arrow points from the red “2” in the expression to the “2” in “215”, an arrow points to the red “1” in the expression to the “1” in “215”, and an arrow points from the red “5” in the expression to the “5” in 215.$

Digit	Place value	Number	Value	Total value
2	hundreds	2	100	200
1	tens	1	10	10
5	ones	5	1	+5
				215

The base-$10$ blocks model the number $215$.

Exercise $\PageIndex{3}$

Use place value notation to find the value of the number modeled by the base-$10$ blocks shown.

$An image consisting of three items. The first item is a square of 100, 10 blocks wide and 10 blocks tall. The second item is 7 horizontal rods containing 10 blocks each. The third item is 6 individual blocks.$

Figure $\PageIndex{6}$

Answer: $176$

Exercise $\PageIndex{4}$

Use place value notation to find the value of the number modeled by the base-$10$ blocks shown.

$An image consisting of three items. The first item is two squares of 100 blocks each, 10 blocks wide and 10 blocks tall. The second item is three horizontal rods containing 10 blocks each. The third item is 7 individual blocks.$

Figure $\PageIndex{7}$

Answer: $237$

Identify the Place Value of a Digit

By looking at money and base-10 blocks, we saw that each place in a number has a different value. A place value chart is a useful way to summarize this information. The place values are separated into groups of three, called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.

Just as with the base-$10$ blocks, where the value of the tens rod is ten times the value of the ones block and the value of the hundreds square is ten times the tens rod, the value of each place in the place-value chart is ten times the value of the place to the right of it.

Figure $\PageIndex{8}$ shows how the number $5,278,194$ is written in a place value chart.

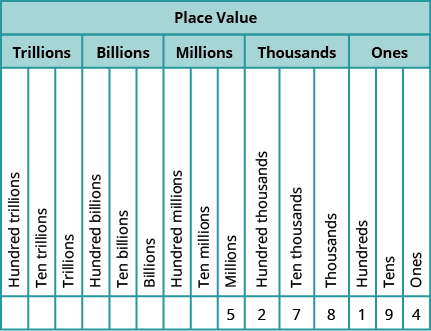
$A chart titled 'Place Value' with fifteen columns and 4 rows, with the columns broken down into five groups of three. The header row shows Trillions, Billions, Millions, Thousands, and Ones. The next row has the values 'Hundred trillions', 'Ten trillions', 'trillions', 'hundred billions', 'ten billions', 'billions', 'hundred millions', 'ten millions', 'millions', 'hundred thousands', 'ten thousands', 'thousands', 'hundreds', 'tens', and 'ones'. The first 8 values in the next row are blank. Starting with the ninth column, the values are '5', '2', '7', '8', '1', '9', and '4'.$

Figure $\PageIndex{8}$

The digit $5$ is in the millions place. Its value is $5,000,000$.
The digit $2$ is in the hundred thousands place. Its value is $200,000$.
The digit $7$ is in the ten thousands place. Its value is $70,000$.
The digit $8$ is in the thousands place. Its value is $8,000$.
The digit $1$ is in the hundreds place. Its value is $100$.
The digit $9$ is in the tens place. Its value is $90$.
The digit $4$ is in the ones place. Its value is $4$.

Example $\PageIndex{3}$: place value

In the number $63,407,218$; find the place value of each of the following digits:

Solution

Write the number in a place value chart, starting at the right.

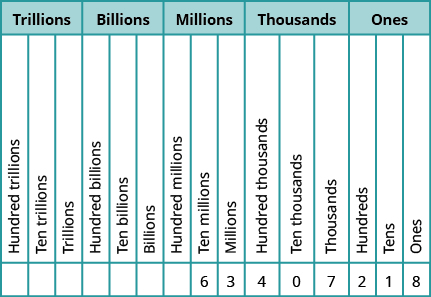
$A figure titled “Place Values” with fifteen columns and 2 rows, with the colums broken down into five groups of three. The first row has the values “Hundred trillions”, “Ten trillions”, “trillions”, “hundred billions”, “ten billions”, “billions”, “hundred millions”, “ten millions”, “millions”, “hundred thuosands”, “ten thousands”, “thousands”, “hundreds”, “tens”, and “ones”. The first 7 values in the second row are blank. Starting with eighth column, the values are “6”, “3”, “4”, “0”, “7”, “2”, “1” and “8”. The first group is labeled “trillions” and contains the first row values of “Hundred trillions”, “ten trillions”, and “trillions”. The second group is labeled “billions” and contains the first row values of “Hundred billions”, “ten billions”, and “billions”. The third group is labeled “millions” and contains the first row values of “Hundred millions”, “ten millions”, and “millions”. The fourth group is labeled “thousands” and contains the first row values of “Hundred thousands”, “ten thousands”, and “thousands”. The fifth group is labeled “ones” and contains the first row values of “Hundreds”, “tens”, and “ones”.$

Figure $\PageIndex{9}$

The $7$ is in the thousands place.
The $0$ is in the ten thousands place.
The $1$ is in the tens place.
The $6$ is in the ten millions place.
The $3$ is in the millions place.

Exercise $\PageIndex{5}$

For each number, find the place value of digits listed: $27,493,615$

$2$
$1$
$4$
$7$
$5$

Answer a: $2$

Answer b: $1$

Answer c: $4$

Answer d: $7$

Answer e: $5$

Exercise $\PageIndex{6}$

For each number, find the place value of digits listed: $519,711,641,328$

$9$
$4$
$2$
$6$
$7$

Answer a: billions

Answer b: ten thousands

Answer c: tens

Answer d: hundred thousands

Answer e: hundred millions

Use Place Value to Name Whole Numbers

When you write a check, you write out the number in words as well as in digits. To write a number in words, write the number in each period followed by the name of the period without the ‘s’ at the end. Start with the digit at the left, which has the largest place value. The commas separate the periods, so wherever there is a comma in the number, write a comma between the words. The ones period, which has the smallest place value, is not named.

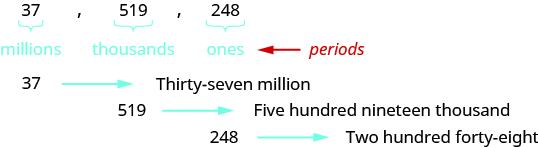
$An image with three values separated by commas. The first value is “37” and has the label “millions”. The second value is “519” and has the label thousands. The third value is “248” and has the label ones. Underneath, the value “37” has an arrow pointing to “Thirty-seven million”, the value “519” has an arrow pointing to “Five hundred nineteen thousand”, and the value “248” has an arrow pointing to “Two hundred forty-eight”.$

So the number $37,519,248$ is written thirty-seven million, five hundred nineteen thousand, two hundred forty-eight. Notice that the word and is not used when naming a whole number.

How to: Name a Whole Number in Words.

Step 1. Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.

Step 2. Use commas in the number to separate the periods.

Example $\PageIndex{4}$: name whole numbers

Name the number $8,165,432,098,710$ in words.

Solution

Begin with the leftmost digit, which is $8$. It is in the trillions place.	eight trillion
The next period to the right is billions.	one hundred sixty-five billion
The next period to the right is millions.	four hundred thirty-two million
The next period to the right is thousands.	ninety-eight thousand
The rightmost period shows the ones.	seven hundred ten

$An image with five values separated by commas. The first value is “8” and has the label “trillions”. The second value is “165” and has the label “bilions”. The third value is “432” and has the label “millions”. The fourth value is “098” and has the label “thousands”. The fifth value is “710” and has the label “ones”. Underneath, the value “8” has an arrow pointing to “Eight trillion”, the value “165” has an arrow pointing to “One hundred sixty-five billion”, the value “432” has an arrow pointing to “Four hundred thirty-two million”, the value “098” has an arrow pointing to “Ninety-eight thousand”, and the value “710” has an arrow pointing to “seven hundred ten”.$

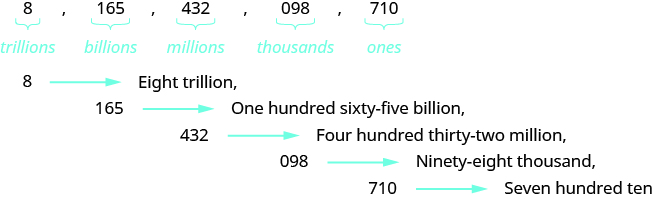
Putting all of the words together, we write $8,165,432,098,710$ as eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.

Exercise $\PageIndex{7}$

Name each number in words: $9,258,137,904,061$

Answer: nine trillion, two hundred fifty-eight billion, one hundred thirty-seven million, nine hundred four thousand, sixty-one

Exercise $\PageIndex{8}$

Name each number in words: $17,864,325,619,004$

Answer: seventeen trillion, eight hundred sixty-four billion, three hundred twenty-five million, six hundred nineteen thousand, four

Example $\PageIndex{5}$: name whole numbers

A student conducted research and found that the number of mobile phone users in the United States during one month in 2014 was $327,577,529$. Name that number in words.

Solution

Identify the periods associated with the number.

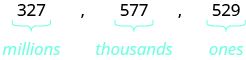
$An image with three values separated by commas. The first value is “327” and has the label “millions”. The second value is “577” and has the label “thousands”. The third value is “529” and has the label “ones”.$

Name the number in each period, followed by the period name. Put the commas in to separate the periods.

Millions period: three hundred twenty-seven million

Thousands period: five hundred seventy-seven thousand

Ones period: five hundred twenty-nine

So the number of mobile phone users in the Unites States during the month of April was three hundred twenty-seven million, five hundred seventy-seven thousand, five hundred twenty-nine.

Exercise $\PageIndex{9}$

The population in a country is $316,128,839$. Name that number

Answer: three hundred sixteen million, one hundred twenty-eight thousand, eight hundred thirty nine

Exercise $\PageIndex{10}$

One year is $31,536,000$ seconds. Name that number.

Answer: thirty one million, five hundred thirty-six thousand

Use Place Value to Write Whole Numbers

We will now reverse the process and write a number given in words as digits.

How to: Use Place Value to Write Whole Numbers

Step 1. Identify the words that indicate periods. (Remember the ones period is never named.)

Step 2. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Step 3. Name the number in each period and place the digits in the correct place value position.

Example $\PageIndex{6}$: write whole numbers

Write the following numbers using digits.

fifty-three million, four hundred one thousand, seven hundred forty-two
nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine

Solution

Identify the words that indicate periods.

Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Then write the digits in each period.

$An image with three blocks of text pointing to numerical values. The first block of text is “fifty-three million”, has the label “millions”, and points to value 53. The second block of text is “four hundred one thousand”, has the label “thousands”, and points to value 401. The third block of text is “seven hundred forty-two”, has the label “ones”, and points to value 742.$

Put the numbers together, including the commas. The number is $53,401,742$.

Identify the words that indicate periods.

Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.

Then write the digits in each period.

$An image with four blocks of text pointing to numerical values. The first block of text is “nine billion”, has the label “billions”, and points to value 9. The second block of text is “two hundred forty-six million”, has the label “millions”, and points to value 246. The third block of text is “seventy-three thousand”, has the label “thousands”, and points to value 742. The fourth block of text is “one hundred eighty-nine”, has the label “ones”, and points to the value 189.$

The number is $9,246,073,189.$

Notice that in part (b), a zero was needed as a place-holder in the hundred thousands place. Be sure to write zeros as needed to make sure that each period, except possibly the first, has three places.

Exercise $\PageIndex{11}$

Write each number in standard form:

fifty-three million, eight hundred nine thousand, fifty-one

Answer: $53,809,051$

Exercise $\PageIndex{12}$

Write each number in standard form:

two billion, twenty-two million, seven hundred fourteen thousand, four hundred sixty-six

Answer: $2,022,714,466$

Example $\PageIndex{7}$: write standard form

A state budget was about $$77$ billion. Write the budget in standard form.

Solution

Identify the periods. In this case, only two digits are given and they are in the billions period. To write the entire number, write zeros for all of the other periods.

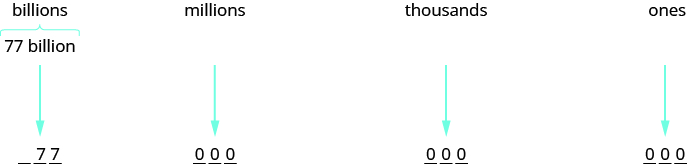
$An image with four blocks of text pointing to numerical values. The first block of text is “77 billion”, has the label “billions”, and points to value “77”. The second block of text is null, has the label “millions”, and points to value “000”. The third block of text is null, has the label “thousands”, and points to value “000”. The fourth block of text is null, has the label “ones”, and points to the value “000”.$

So the budget was about $$77,000,000,000$.

Exercise $\PageIndex{13}$

Write each number in standard form:

The closest distance from Earth to Mars is about $34$ million miles.

Answer: $34,000,000\: miles$

Exercise $\PageIndex{14}$

Write each number in standard form:

The total weight of an aircraft carrier is $204$ million pounds.

Answer: $204,000,000\: pounds$

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.

Search

Text Color

Text Size

Margin Size

Font Type

Definition: Counting Numbers

Definition: Whole Numbers

Example \(\PageIndex{1}\): Number Identification

Exercise \(\PageIndex{1}\)

Exercise \(\PageIndex{2}\)

Example \(\PageIndex{2}\): place value notation

Exercise \(\PageIndex{3}\)

Exercise \(\PageIndex{4}\)

Example \(\PageIndex{3}\): place value

Exercise \(\PageIndex{5}\)

Exercise \(\PageIndex{6}\)

How to: Name a Whole Number in Words.

Example \(\PageIndex{4}\): name whole numbers

Exercise \(\PageIndex{7}\)

Exercise \(\PageIndex{8}\)

Example \(\PageIndex{5}\): name whole numbers

Exercise \(\PageIndex{9}\)

Exercise \(\PageIndex{10}\)

How to: Use Place Value to Write Whole Numbers

Example \(\PageIndex{6}\): write whole numbers

Exercise \(\PageIndex{11}\)

Exercise \(\PageIndex{12}\)

Example \(\PageIndex{7}\): write standard form

Exercise \(\PageIndex{13}\)

Exercise \(\PageIndex{14}\)