1.1: Introduction to Whole Numbers (Part 1)
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Identify counting numbers and whole numbers
- Model whole numbers
- Identify the place value of a digit
- Use place value to name whole numbers
- Use place value to write whole numbers
- Round whole numbers
Identify Counting Numbers and Whole Numbers
Learning algebra is similar to learning a language. You start with a basic vocabulary and then add to it as you go along. You need to practice often until the vocabulary becomes easy to you. The more you use the vocabulary, the more familiar it becomes.
Algebra uses numbers and symbols to represent words and ideas. Let’s look at the numbers first. The most basic numbers used in algebra are those we use to count objects: 1,2,3,4,5,… and so on. These are called the counting numbers. The notation “…” is called an ellipsis, which is another way to show “and so on”, or that the pattern continues endlessly. Counting numbers are also called natural numbers.
The counting numbers start with 1 and continue.
1,2,3,4,5…
Counting numbers and whole numbers can be visualized on a number line as shown in Figure 1.1.1.

Figure 1.1.1: The numbers on the number line increase from left to right, and decrease from right to left.
The point labeled 0 is called the origin. The points are equally spaced to the right of 0 and labeled with the counting numbers. When a number is paired with a point, it is called the coordinate of the point.
The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called the whole numbers.
The whole numbers are the counting numbers and zero.
0,1,2,3,4,5…
We stopped at 5 when listing the first few counting numbers and whole numbers. We could have written more numbers if they were needed to make the patterns clear.
Which of the following are
- counting numbers
- whole numbers
0,14,3,5.2,15,105
Solution
- The counting numbers start at 1, so 0 is not a counting number. The numbers 3, 15, and 105 are all counting numbers.
- Whole numbers are counting numbers and 0. The numbers 0,3,15, and 105 are whole numbers. The numbers 14 and 5.2 are neither counting numbers nor whole numbers. We will discuss these numbers later.
Which of the following are
- whole numbers
0,23,2,9,11.8,241,376
- Answer a
-
2,9,241,376
- Answer b
-
0,2,9,241,376
Which of the following are
- counting numbers
- whole numbers
0,53,7,8.8,13,201
- Answer a
-
7,13,201
- Answer b
-
0,7,13,201
Model Whole Numbers
Our number system is called a place value system because the value of a digit depends on its position, or place, in a number. The number 537 has a different value than the number 735. Even though they use the same digits, their value is different because of the different placement of the 3 and the 7 and the 5.
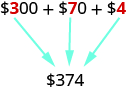
Money gives us a familiar model of place value. Suppose a wallet contains three $100 bills, seven $10 bills, and four $1 bills. The amounts are summarized in Figure 1.1.2. How much money is in the wallet?

Figure 1.1.2
Find the total value of each kind of bill, and then add to find the total. The wallet contains $374.
Base-10 blocks provide another way to model place value, as shown in Figure 1.1.3. The blocks can be used to represent hundreds, tens, and ones. Notice that the tens rod is made up of 10 ones, and the hundreds square is made of 10 tens, or 100 ones.
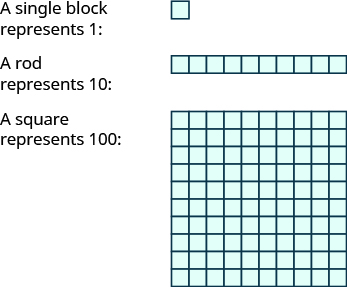
Figure 1.1.3
Figure 1.1.4 shows the number 138 modeled with base-10 blocks.
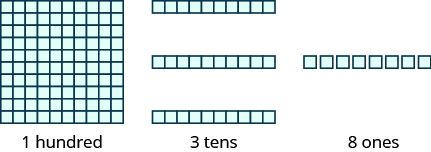
Figure 1.1.4: We use place value notation to show the value of the number 138.

| Digit | Place value | Number | Value | Total value |
|---|---|---|---|---|
| 1 | hundreds | 1 | 100 | 100 |
| 3 | tens | 3 | 10 | 30 |
| 8 | ones | 8 | 1 | +8 |
| Sum = | 138 |
Use place value notation to find the value of the number modeled by the base-10 blocks shown.

Figure 1.1.5
Solution
There are 2 hundreds squares, which is 200.
There is 1 tens rod, which is 10.
There are 5 ones blocks, which is 5.
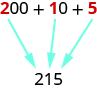
| Digit | Place value | Number | Value | Total value |
|---|---|---|---|---|
| 2 | hundreds | 2 | 100 | 200 |
| 1 | tens | 1 | 10 | 10 |
| 5 | ones | 5 | 1 | +5 |
| 215 |
The base-10 blocks model the number 215.
Use place value notation to find the value of the number modeled by the base-10 blocks shown.

Figure 1.1.6
- Answer
-
176
Use place value notation to find the value of the number modeled by the base-10 blocks shown.

Figure 1.1.7
- Answer
-
237
Identify the Place Value of a Digit
By looking at money and base-10 blocks, we saw that each place in a number has a different value. A place value chart is a useful way to summarize this information. The place values are separated into groups of three, called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.
Just as with the base-10 blocks, where the value of the tens rod is ten times the value of the ones block and the value of the hundreds square is ten times the tens rod, the value of each place in the place-value chart is ten times the value of the place to the right of it.
Figure 1.1.8 shows how the number 5,278,194 is written in a place value chart.
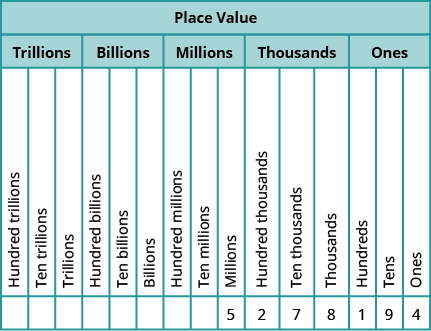
Figure 1.1.8
- The digit 5 is in the millions place. Its value is 5,000,000.
- The digit 2 is in the hundred thousands place. Its value is 200,000.
- The digit 7 is in the ten thousands place. Its value is 70,000.
- The digit 8 is in the thousands place. Its value is 8,000.
- The digit 1 is in the hundreds place. Its value is 100.
- The digit 9 is in the tens place. Its value is 90.
- The digit 4 is in the ones place. Its value is 4.
In the number 63,407,218; find the place value of each of the following digits:
- 7
- 0
- 1
- 6
- 3
Solution
Write the number in a place value chart, starting at the right.
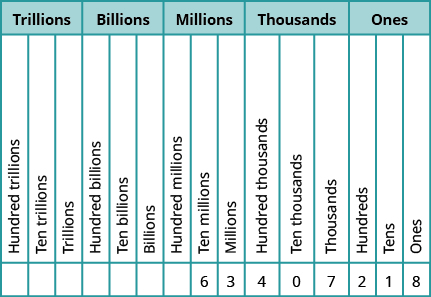
Figure 1.1.9
- The 7 is in the thousands place.
- The 0 is in the ten thousands place.
- The 1 is in the tens place.
- The 6 is in the ten millions place.
- The 3 is in the millions place.
For each number, find the place value of digits listed: 27,493,615
- 2
- 1
- 4
- 7
- 5
- Answer a
-
2
- Answer b
-
1
- Answer c
-
4
- Answer d
-
7
- Answer e
-
5
For each number, find the place value of digits listed: 519,711,641,328
- 9
- 4
- 2
- 6
- 7
- Answer a
-
billions
- Answer b
-
ten thousands
- Answer c
-
tens
- Answer d
-
hundred thousands
- Answer e
-
hundred millions
Use Place Value to Name Whole Numbers
When you write a check, you write out the number in words as well as in digits. To write a number in words, write the number in each period followed by the name of the period without the ‘s’ at the end. Start with the digit at the left, which has the largest place value. The commas separate the periods, so wherever there is a comma in the number, write a comma between the words. The ones period, which has the smallest place value, is not named.
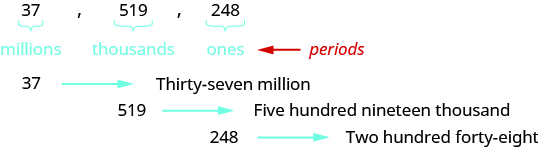
So the number 37,519,248 is written thirty-seven million, five hundred nineteen thousand, two hundred forty-eight. Notice that the word and is not used when naming a whole number.
Step 1. Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.
Step 2. Use commas in the number to separate the periods.
Name the number 8,165,432,098,710 in words.
Solution
| Begin with the leftmost digit, which is 8. It is in the trillions place. | eight trillion |
| The next period to the right is billions. | one hundred sixty-five billion |
| The next period to the right is millions. | four hundred thirty-two million |
| The next period to the right is thousands. | ninety-eight thousand |
| The rightmost period shows the ones. | seven hundred ten |
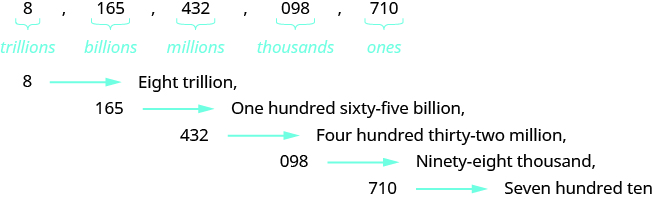
Putting all of the words together, we write 8,165,432,098,710 as eight trillion, one hundred sixty-five billion, four hundred thirty-two million, ninety-eight thousand, seven hundred ten.
Name each number in words: 9,258,137,904,061
- Answer
-
nine trillion, two hundred fifty-eight billion, one hundred thirty-seven million, nine hundred four thousand, sixty-one
Name each number in words: 17,864,325,619,004
- Answer
-
seventeen trillion, eight hundred sixty-four billion, three hundred twenty-five million, six hundred nineteen thousand, four
A student conducted research and found that the number of mobile phone users in the United States during one month in 2014 was 327,577,529. Name that number in words.
Solution
Identify the periods associated with the number.
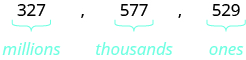
Name the number in each period, followed by the period name. Put the commas in to separate the periods.
Millions period: three hundred twenty-seven million
Thousands period: five hundred seventy-seven thousand
Ones period: five hundred twenty-nine
So the number of mobile phone users in the Unites States during the month of April was three hundred twenty-seven million, five hundred seventy-seven thousand, five hundred twenty-nine.
The population in a country is 316,128,839. Name that number
- Answer
-
three hundred sixteen million, one hundred twenty-eight thousand, eight hundred thirty nine
One year is 31,536,000 seconds. Name that number.
- Answer
-
thirty one million, five hundred thirty-six thousand
Use Place Value to Write Whole Numbers
We will now reverse the process and write a number given in words as digits.
Step 1. Identify the words that indicate periods. (Remember the ones period is never named.)
Step 2. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
Step 3. Name the number in each period and place the digits in the correct place value position.
Write the following numbers using digits.
- fifty-three million, four hundred one thousand, seven hundred forty-two
- nine billion, two hundred forty-six million, seventy-three thousand, one hundred eighty-nine
Solution
- Identify the words that indicate periods.
Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
Then write the digits in each period.

Put the numbers together, including the commas. The number is 53,401,742.
- Identify the words that indicate periods.
Except for the first period, all other periods must have three places. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
Then write the digits in each period.

The number is 9,246,073,189.
Notice that in part (b), a zero was needed as a place-holder in the hundred thousands place. Be sure to write zeros as needed to make sure that each period, except possibly the first, has three places.
Write each number in standard form:
fifty-three million, eight hundred nine thousand, fifty-one
- Answer
-
53,809,051
Write each number in standard form:
two billion, twenty-two million, seven hundred fourteen thousand, four hundred sixty-six
- Answer
-
2,022,714,466
A state budget was about $77 billion. Write the budget in standard form.
Solution
Identify the periods. In this case, only two digits are given and they are in the billions period. To write the entire number, write zeros for all of the other periods.
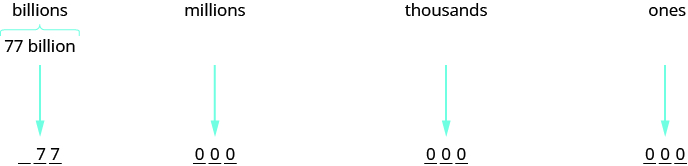
So the budget was about $77,000,000,000.
Write each number in standard form:
The closest distance from Earth to Mars is about 34 million miles.
- Answer
-
34,000,000miles
Write each number in standard form:
The total weight of an aircraft carrier is 204 million pounds.
- Answer
-
204,000,000pounds
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


