1.7: Multiply Whole Numbers (Part 1)
- Page ID
- 4973
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use multiplication notation
- Model multiplication of whole numbers
- Multiply whole numbers
- Translate word phrases to math notation
- Multiply whole numbers in applications
Before you get started, take this readiness quiz.
- Add: \(1,683 + 479\). If you missed this problem, review Example 1.2.10.
- Subtract: \(605 − 321\). If you missed this problem, review Example 1.3.4.
Use Multiplication Notation
Suppose you were asked to count all these pennies shown in Figure \(\PageIndex{1}\).

Figure \(\PageIndex{1}\)
Would you count the pennies individually? Or would you count the number of pennies in each row and add that number \(3\) times.
\[8 + 8 + 8 \nonumber\]
Multiplication is a way to represent repeated addition. So instead of adding \(8\) three times, we could write a multiplication expression.
\[3 \times 8 \nonumber \]
We call each number being multiplied a factor and the result the product. We read \(3 × 8\) as three times eight, and the result as the product of three and eight.
There are several symbols that represent multiplication. These include the symbol × as well as the dot, • , and parentheses ( ).
To describe multiplication, we can use symbols and words.
| Operation | Notation | Expression | Read as | Result |
|---|---|---|---|---|
| Multiplication | × | 3 × 8 | three times eight | the product of 3 and 8 |
| • | 3 • 8 | |||
| () | 3(8) |
Translate from math notation to words:
- \(7 × 6\)
- \(12 · 14\)
- \(6(13)\)
Solution
- We read this as seven times six and the result is the product of seven and six.
- We read this as twelve times fourteen and the result is the product of twelve and fourteen.
- We read this as six times thirteen and the result is the product of six and thirteen.
Translate from math notation to words:
- \(8 × 7\)
- \(18 • 11\)
- Answer a
-
eight times seven ; the product of eight and seven
- Answer b
-
eighteen times eleven ; the product of eighteen and eleven
Translate from math notation to words:
- \((13)(7)\)
- \(5(16)\)
- Answer a
-
thirteen times seven ; the product of thirteen and seven
- Answer b
-
five times sixteen; the product of five and sixteen
Model Multiplication of Whole Numbers
There are many ways to model multiplication. Unlike in the previous sections where we used base-\(10\) blocks, here we will use counters to help us understand the meaning of multiplication. A counter is any object that can be used for counting. We will use round blue counters.
Model: \(3 × 8\).
Solution
To model the product \(3 × 8\), we’ll start with a row of \(8\) counters.

The other factor is \(3\), so we’ll make \(3\) rows of \(8\) counters.

Now we can count the result. There are \(24\) counters in all.
\[3 \times 8 = 24 \nonumber \]
If you look at the counters sideways, you’ll see that we could have also made \(8\) rows of \(3\) counters. The product would have been the same. We’ll get back to this idea later.
Model each multiplication: \(4 × 6\).
- Answer
-

Model each multiplication: \(5 × 7\).
- Answer
-

Multiply Whole Numbers
In order to multiply without using models, you need to know all the one digit multiplication facts. Make sure you know them fluently before proceeding in this section. Table \(\PageIndex{2}\) shows the multiplication facts. Each box shows the product of the number down the left column and the number across the top row. If you are unsure about a product, model it. It is important that you memorize any number facts you do not already know so you will be ready to multiply larger numbers.
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
What happens when you multiply a number by zero? You can see that the product of any number and zero is zero. This is called the Multiplication Property of Zero.
The product of any number and \(0\) is \(0\).
\[a \cdot 0 = 0\]
\[0 \cdot a = 0\]
Multiply:
- \(0 • 11\)
- \((42)0\)
Solution
| The product of any number and zero is zero. | 0 • 11 = 0 |
| Multiplying by zero results in zero. | (42)0 = 0 |
Find each product:
- \(0 • 19\)
- \((39)0\)
- Answer a
-
\(0\)
- Answer b
-
\(0\)
Find each product:
- \(0 • 24\)
- \((57)0\)
- Answer a
-
\(0\)
- Answer b
-
\(0\)
What happens when you multiply a number by one? Multiplying a number by one does not change its value. We call this fact the Identity Property of Multiplication, and \(1\) is called the multiplicative identity.
The product of any number and \(1\) is the number.
\[1 \cdot a = a\]
\[a \cdot 1 = a\]
Multiply:
- \((11)1\)
- \(1 • 42\)
Solution
| The product of any number and one is the number. | (11)1 = 11 |
| Multiplying by one does not change the value. | 1 • 42 = 42 |
Find each product:
- \((19)1\)
- \(1 • 39\)
- Answer a
-
\(19\)
- Answer b
-
\(39\)
Find each product:
- \((24)(1)\)
- \(1 × 57\)
- Answer a
-
\(24\)
- Answer b
-
\(57\)
Earlier in this chapter, we learned that the Commutative Property of Addition states that changing the order of addition does not change the sum. We saw that \(8 + 9 = 17\) is the same as \(9 + 8 = 17\).
Is this also true for multiplication? Let’s look at a few pairs of factors.
\[\begin{split} 4 \cdot 7 & = 28 \qquad 7 \cdot 4 = 28 \\ 9 \cdot 7 & = 63 \qquad 7 \cdot 9 = 63 \\ 8 \cdot 9 & = 72 \qquad 9 \cdot 8 = 72 \end{split}\]
When the order of the factors is reversed, the product does not change. This is called the Commutative Property of Multiplication.
Changing the order of the factors does not change their product.
\[a \cdot b = b \cdot a\]
Multiply:
- \(8 • 7\)
- \(7 • 8\)
Solution
| Multiply. | 8 • 7 = 56 |
| Multiply. | 7 • 8 = 56 |
Changing the order of the factors does not change the product.
Multiply:
- \(9 • 6\)
- \(6 • 9\)
- Answer a
-
\(54\)
- Answer b
-
\(54\)
Multiply:
- \(8 • 6\)
- \(6 • 8\)
- Answer a
-
\(48\)
- Answer b
-
\(48\)
To multiply numbers with more than one digit, it is usually easier to write the numbers vertically in columns just as we did for addition and subtraction.
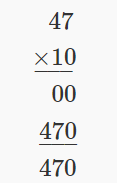
We start by multiplying \(3\) by \(7\).
\[3 \times 7 = 21 \nonumber \]
We write the \(1\) in the ones place of the product. We carry the \(2\) tens by writing \(2\) above the tens place.
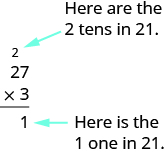
Then we multiply the \(3\) by the \(2\), and add the \(2\) above the tens place to the product. So \(3 × 2 = 6\), and \(6 + 2 = 8\). Write the \(8\) in the tens place of the product.

The product is \(81\).
When we multiply two numbers with a different number of digits, it’s usually easier to write the smaller number on the bottom. You could write it the other way, too, but this way is easier to work with.
Multiply: \(15 • 4\).
Solution
| Write the numbers so the digits 5 and 4 line up vertically. | 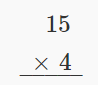 |
| Multiply 4 by the digit in the ones place of 15. 4 • 5 = 20. | |
| Write 0 in the ones place of the product and carry the 2 tens. | 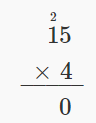 |
| Multiply 4 by the digit in the tens place of 15. 4 ⋅ 1 = 4. Add the 2 tens we carried. 4 + 2 = 6. | |
| Write the 6 in the tens place of the product. | 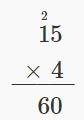 |
Multiply: \(64 • 8\).
- Answer
-
\(512\)
Multiply: \(57 • 6\).
- Answer
-
\(342\)
Multiply: \(286 • 5\).
Solution
| Write the numbers so the digits 5 and 6 line up vertically. | 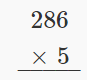 |
| Multiply 5 by the digit in the ones place of 286. 5 • 6 = 30. | |
| Write the 0 in the ones place of the product and carry the 3 to the tens place. Multiply 5 by the digit in the tens place of 286. 5 • 8 = 40. | 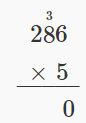 |
| Add the 3 tens we carried to get 40 + 3 = 43. Write the 3 in the tens place of the product and carry the 4 to the hundreds place. | 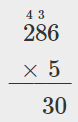 |
| Multiply 5 by the digit in the hundreds place of 286. 5 • 2 = 10. Add the 4 hundreds we carried to get 10 + 4 = 14. Write the 4 in the hundreds place of the product and the 1 to the thousands place. | 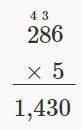 |
Multiply: \(347 • 5\).
- Answer
-
\(1,735\)
Multiply: \(462 • 7\).
- Answer
-
\(3,234\)
When we multiply by a number with two or more digits, we multiply by each of the digits separately, working from right to left. Each separate product of the digits is called a partial product. When we write partial products, we must make sure to line up the place values.
Step 1. Write the numbers so each place value lines up vertically.
Step 2. Multiply the digits in each place value.
- Work from right to left, starting with the ones place in the bottom number.
- Multiply the bottom number by the ones digit in the top number, then by the tens digit, and so on.
- If a product in a place value is more than 9, carry to the next place value.
- Write the partial products, lining up the digits in the place values with the numbers above.
- Repeat for the tens place in the bottom number, the hundreds place, and so on.
- Insert a zero as a placeholder with each additional partial product.
Step 3. Add the partial products.
Multiply: \(62(87)\).
Solution
| Write the numbers so each place lines up vertically | 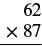 |
| Start by multiplying 7 by 62. Multiply 7 by the digit in the ones place of 62. 7 • 2 = 14. Write the 4 in the ones place of the product and carry the 1 to the tens place. |  |
| Multiply 7 by the digit in the tens place of 62. 7 • 6 = 42. Add the 1 ten we carried. 42 + 1 = 43. Write the 3 in the tens place of the product and the 4 in the hundreds place. | 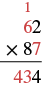 |
| The first partial product is 434. | |
| Now, write a 0 under the 4 in the ones place of the next partial product as a placeholder since we now multiply the digit in the tens place of 87 by 62. Multiply 8 by the digit in the ones place of 62. 8 • 2 = 16. Write the 6 in the next place of the product, which is the tens place. Carry the 1 to the tens place. |  |
| Multiply 8 by 6, the digit in the tens place of 62, then add the 1 ten we carried to get 49. Write the 9 in the hundreds place of the product and the 4 in the thousands place. |  |
| The second partial product is 4960. Add the partial products. |  |
The product is \(5,394\).
Multiply: \(43(78)\).
- Answer
-
\(3,354\)
Multiply: \(64(59)\).
- Answer
-
\(3,776\)
Multiply:
- \(47 • 10\)
- \(47 • 100\)
Solution
| (a) 47 • 10 | 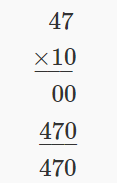 |
| (b) 47 • 100 | 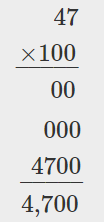 |
When we multiplied \(47\) times \(10\), the product was \(470\). Notice that \(10\) has one zero, and we put one zero after \(47\) to get the product. When we multiplied \(47\) times \(100\), the product was \(4,700\). Notice that \(100\) has two zeros and we put two zeros after \(47\) to get the product.
Do you see the pattern? If we multiplied \(47\) times \(10,000\), which has four zeros, we would put four zeros after \(47\) to get the product \(470,000\).
Multiply:
- \(54 • 10\)
- \(54 • 100\)
- Answer a
-
\(540\)
- Answer b
-
\(5,400\)
Multiply:
- \(75 • 10\)
- \(75 • 100\)
- Answer
-
\(750\)
- Answer
-
\(7,500\)
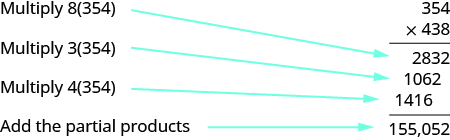
Multiply: \(354(438)\).
Solution
There are three digits in the factors so there will be \(3\) partial products. We do not have to write the \(0\) as a placeholder as long as we write each partial product in the correct place.
Multiply: \(265(483)\).
- Answer
-
\(127,995\)
Multiply: \(823(794)\).
- Answer
-
\(653,462\)
Multiply: \(896(201)\).
Solution
There should be \(3\) partial products. The second partial product will be the result of multiplying \(896\) by \(0\).
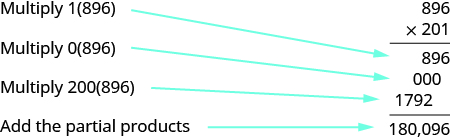
Notice that the second partial product of all zeros doesn’t really affect the result. We can place a zero as a placeholder in the tens place and then proceed directly to multiplying by the \(2\) in the hundreds place, as shown.
Multiply by \(10\), but insert only one zero as a placeholder in the tens place. Multiply by \(200\), putting the \(2\) from the \(12\). \(2 • 6 = 12\) in the hundreds place.
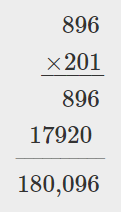
Multiply: \((718)509\).
- Answer
-
\(365,462\)
Multiply: \((627)804\).
- Answer
-
\(504,108\)
When there are three or more factors, we multiply the first two and then multiply their product by the next factor. For example:
| to multiply | 8 • 3 • 2 |
| first multiply 8 • 3 | 24 • 2 |
| then multiply 24 • 2 | 48 |
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


