1.3: Add Whole Numbers (Part 1)
- Page ID
- 4971
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use addition notation
- Model addition of whole numbers
- Add whole numbers without models
- Translate word phrases to math notation
- Add whole numbers in applications
Before you get started, take this readiness quiz.
- What is the number modeled by the base-\(10\) blocks? If you missed this problem, review Example 1.1.2.

Figure \(\PageIndex{1}\)
- Write the number three hundred forty-two thousand six using digits? If you missed this problem, review Example 1.1.6.
Use Addition Notation
A college student has a part-time job. Last week he worked \(3\) hours on Monday and \(4\) hours on Friday. To find the total number of hours he worked last week, he added \(3\) and \(4\).
The operation of addition combines numbers to get a sum. The notation we use to find the sum of \(3\) and \(4\) is:
\[3 + 4 \nonumber \]
We read this as three plus four and the result is the sum of three and four. The numbers \(3\) and \(4\) are called the addends. A math statement that includes numbers and operations is called an expression.
To describe addition, we can use symbols and words.
| Operation | Notation | Expression | Read as | Result |
|---|---|---|---|---|
| Addition | + | 3+4 | three plus four | the sum of 3 and 4 |
Translate from math notation to words:
- \(7 + 1\)
- \(12 + 14\)
Solution
- The expression consists of a plus symbol connecting the addends \(7\) and \(1\). We read this as seven plus one. The result is the sum of seven and one.
- The expression consists of a plus symbol connecting the addends \(12\) and \(14\). We read this as twelve plus fourteen. The result is the sum of twelve and fourteen.
Translate from math notation to words:
- \(8 + 4\)
- \(18 + 11\)
- Answer a
-
eight plus four; the sum of eight and four
- Answer b
-
eighteen plus eleven; the sum of eighteen and eleven
Translate from math notation to words:
- \(21 + 16\)
- \(100 + 200\)
- Answer a
-
twenty-one plus sixteen; the sum of twenty-one and sixteen
- Answer b
-
one hundred plus two hundred; the sum of one hundred and two hundred
Model Addition of Whole Numbers
Addition is really just counting. We will model addition with base-\(10\) blocks. Remember, a block represents \(1\) and a rod represents \(10\). Let’s start by modeling the addition expression we just considered, \(3 + 4\).
Each addend is less than 10, so we can use ones blocks.
|
We start by modeling the first number with 3 blocks. |
 |
|
Then we model the second number with 4 blocks. |
 |
|
Count the total number of blocks. |
 |
There are \(7\) blocks in all. We use an equal sign (\(=\)) to show the sum. A math sentence that shows that two expressions are equal is called an equation. We have shown that \(3 + 4 = 7\).
Model the addition \(2 + 6\).
Solution
\(2 + 6\) means the sum of \(2\) and \(6\)
Each addend is less than \(10\), so we can use ones blocks.
| Model the first number with 2 blocks. |  |
| Model the second number with 6 blocks. |  |
| Count the total number of blocks |  |
| There are 8 blocks in all, so 2 + 6 = 8. |
Model: \(3 + 6\).
- Answer
-
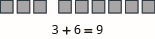
Model: \(5 + 1\).
- Answer
-
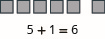
When the result is \(10\) or more ones blocks, we will exchange the \(10\) blocks for one rod.
Model the addition \(5 + 8\).
Solution
\(5 + 8\) means the sum of \(5\) and \(8\).
| Each addend is less than 10, se we can use ones blocks. | |
| Model the first number with 5 blocks. |  |
| Model the second number with 8 blocks. |  |
| Count the result. There are more than 10 blocks so we exchange 10 ones blocks for 1 tens rod. | 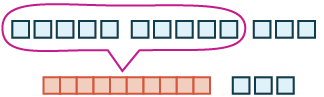 |
| Now we have 1 ten and 3 ones, which is 13. | $$5 + 8 = 13$$ |
Notice that we can describe the models as ones blocks and tens rods, or we can simply say ones and tens. From now on, we will use the shorter version but keep in mind that they mean the same thing.
Model the addition: \(5 + 7\)
- Answer
-
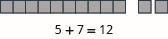
Model the addition: \(6 + 8\).
- Answer
-
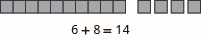
Model the addition: \(17 + 26\).
Solution
\(17 + 26\) means the sum of \(17\) and \(26\).
| Model the 17. | 1 ten and 7 ones |  |
| Model the 26. | 2 tens and 6 ones |  |
| Combine. | 3 tens and 13 ones |  |
| Exchange 10 ones for 1 ten. |
4 tens and 3 ones 40 + 3 = 43 |
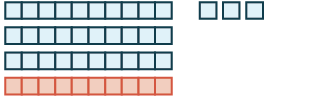 |
| We have shown that 17 + 26 = 43 |
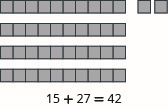
Model each addition: \(15 + 27\).
- Answer
-
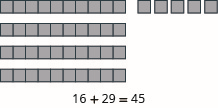
Model each addition: \(16 + 29\).
- Answer
-
Add Whole Numbers Without Models
Now that we have used models to add numbers, we can move on to adding without models. Before we do that, make sure you know all the one digit addition facts. You will need to use these number facts when you add larger numbers.
Imagine filling in Table \(\PageIndex{1}\) by adding each row number along the left side to each column number across the top. Make sure that you get each sum shown. If you have trouble, model it. It is important that you memorize any number facts you do not already know so that you can quickly and reliably use the number facts when you add larger numbers.
| + | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 4 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 5 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 6 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 7 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 8 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 9 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Did you notice what happens when you add zero to a number? The sum of any number and zero is the number itself. We call this the Identity Property of Addition. Zero is called the additive identity.
The sum of any number \(a\) and \(0\) is the number.
\[a + 0 = a\]
\[0 + a = a\]
Find each sum:
- \(0 + 11\)
- \(42 + 0\)
Solution
|
0 + 11 = 11 |
|
42 + 0 = 42 |
Find each sum:
- \(0 + 19\)
- \(39 + 0\)
- Answer a
-
\(0+19=19\)
- Answer b
-
\(39+0=39\)
Find each sum:
- \(0 + 24\)
- \(57 + 0\)
- Answer a
-
\(0+24=24\)
- Answer b
-
\(57+0=57\)
Look at the pairs of sums.
| 2 + 3 = 5 | 3 + 2 = 5 |
| 4 + 7 = 11 | 7 + 4 = 11 |
| 8 + 9 = 17 | 9 + 8 = 17 |
Notice that when the order of the addends is reversed, the sum does not change. This property is called the Commutative Property of Addition, which states that changing the order of the addends does not change their sum.
Changing the order of the addends a and b does not change their sum.
\[a + b = b + a\]
Add:
- \(8 + 7\)
- \(7 + 8\)
Solution
- \(\begin{align*} 8+7 & \\ 15 & \end{align*}\)
- \(\begin{align*} 7 + 8 & \\ 15 & \end{align*}\)
Add: \(9 + 7\) and \(7 + 9\).
- Answer
-
\(9+7=16; 7+9=16\)
Add: \(8 + 6\) and \(6 + 8\).
- Answer
-
\(8+6=14; 6+8=14\)
Add: \(28 + 61\).
Solution
To add numbers with more than one digit, it is often easier to write the numbers vertically in columns.
| Write the numbers so the ones and tens digits line up vertically. | 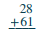 |
| Then add the digits in each place value. Add the ones: 8 + 1 = 9. | 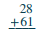 |
| Add the tens: 2 + 6 = 8. | 89 |
Add: \(32 + 54\).
- Answer
-
\(32+54=86\)
Add: \(25 + 74\).
- Answer
-
\(25+74=99\)
In the previous example, the sum of the ones and the sum of the tens were both less than \(10\). But what happens if the sum is \(10\) or more? Let’s use our base-\(10\) model to find out. Figure \(\PageIndex{2}\) shows the addition of \(17\) and \(26\) again.
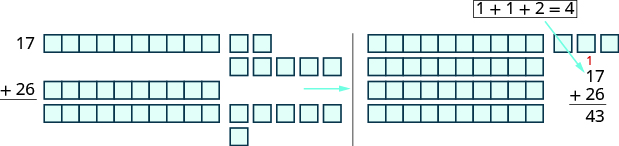
Figure \(\PageIndex{2}\)
When we add the ones, \(7 + 6\), we get \(13\) ones. Because we have more than \(10\) ones, we can exchange \(10\) of the ones for \(1\) ten. Now we have \(4\) tens and \(3\) ones. Without using the model, we show this as a small red \(1\) above the digits in the tens place.
When the sum in a place value column is greater than \(9\), we carry over to the next column to the left. Carrying is the same as regrouping by exchanging. For example, \(10\) ones for \(1\) ten or \(10\) tens for \(1\) hundred.
Step 1. Write the numbers so each place value lines up vertically.
Step 2. Add the digits in each place value. Work from right to left starting with the ones place. If a sum in a place value is more than \(9\), carry to the next place value.
Step 3. Continue adding each place value from right to left, adding each place value and carrying if needed.
Add: \(43 + 69\).
Solution
| Write the numbers so the digits line up vertically. | 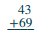 |
| Add the digits in each place. Add the ones: 3 + 9 = 12. | |
| Write the 2 in the ones place in the sum. Add the 1 ten to the tens place. | .png?revision=1&size=bestfit&width=41&height=58) |
| Now add the tens: 1 + 4 + 6 = 11. Write the 11 in the sum. | .png?revision=1&size=bestfit&width=52&height=58) |
Add: \(35 + 98\).
- Answer
-
\(35+98=133\)
Add: \(72 + 89\).
- Answer
-
\(72+89=161\)
Add: \(324 + 586\).
Solution
| Write the numbers so the digits line up vertically. | 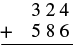 |
| Add the digits in each place value. Add the ones: 4 + 6 = 10. Write the 0 in the ones place in the sum and carry the 1 ten to the tens place. | 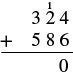 |
| Add the tens: 1 + 2 + 8 = 11. Write the 1 in the tens place in the sum and carry the 1 hundred to the hundreds. | 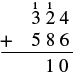 |
| Add the hundreds: 1 + 3 + 5 = 9. Write the 9 in the hundreds place. | 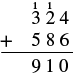 |
Add: \(456 + 376\).
- Answer
-
\(456+376=832\)
Add: \(269 + 578\).
- Answer
-
\(269+578=847\)
Add: \(1,683 + 479\).
Solution
| Write the numbers so the digits line up vertically. | 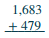.png?revision=1&size=bestfit&width=49&height=38) |
| Add the digits in each place value | |
| Add the ones: 3 + 9 = 12. Write the 2 in the ones place of the sum and carry the 1 ten to the tens place. | 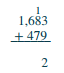.png?revision=1&size=bestfit&width=64&height=73) |
| Add the tens: 1 + 7 + 8 = 16. Write the 6 in the tens place and carry the 1 hundred to the hundreds place. | 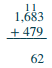.png?revision=1&size=bestfit&width=52&height=68) |
| Add the hundreds: 1 + 6 + 4 = 11. Write the 1 in the hundreds place and carry the 1 thousand to the thousands place | 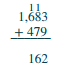.png?revision=1&size=bestfit&width=60&height=66) |
| Add the thousands 1 + 1 = 2. Write the 2 in the thousands place of the sum. | .png?revision=1&size=bestfit&width=57&height=75) |
When the addends have different numbers of digits, be careful to line up the corresponding place values starting with the ones and moving toward the left.
Add: \(4,597 + 685\).
- Answer
-
\(4,597+685=5,282\)
Add: \(5,837 + 695\).
- Answer
-
\(5,837+695=6,532\)
Add: \(21,357 + 861 + 8,596\).
Solution
| Write the numbers so the place values line up vertically. | .png?revision=1&size=bestfit&width=68&height=60) |
| Add the digits in each place value. | |
| Add the ones: 7 + 1 + 6 = 14. Write the 4 in the ones place of the sum and carry the 1 to the tens place. | .png?revision=1&size=bestfit&width=69&height=90) |
| Add the tens: 1 + 5 + 6 + 9 = 21. Write the 1 in the tens place and carry the 2 to the hundreds place. | .png?revision=1&size=bestfit&width=65&height=85) |
| Add the hundreds: 2 + 3 + 8 + 5 = 18. Write the 8 in the hundreds place and carry the 1 to the thousands place. | .png?revision=1&size=bestfit&width=74&height=86) |
| Add the thousands 1 + 1 + 8 = 10. Write the 0 in the thousands place and carry the 1 to the ten thousands place. | .png?revision=1&size=bestfit&width=68&height=85) |
| Add the ten-thousands 1 + 2 = 3. Write the 3 in the ten thousands place in the sum. | 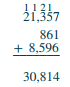.png?revision=1&size=bestfit&width=70&height=87) |
This example had three addends. We can add any number of addends using the same process as long as we are careful to line up the place values correctly.
Add: \(46,195 + 397 + 6,281\).
- Answer
-
\(46,195 + 397 + 6,281=52,873\)
Add: \(53,762 + 196 + 7,458\).
- Answer
-
\(53,762 + 196 + 7,458=61,416\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


