1.5: Subtract Whole Numbers (Part 1)
- Page ID
- 4972
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Use subtraction notation
- Model subtraction of whole numbers
- Subtract whole numbers
- Translate word phrases to math notation
- Subtract whole numbers in applications
Before you get started, take this readiness quiz.
- Model \(3 + 4\) using base-ten blocks. If you missed this problem, review Section 1.2: Add Whole Numbers
- Add: \(324 + 586\). If you missed this problem, review Example 1.2.9.
Use Subtraction Notation
Suppose there are seven bananas in a bowl. Elana uses three of them to make a smoothie. How many bananas are left in the bowl? To answer the question, we subtract three from seven. When we subtract, we take one number away from another to find the difference. The notation we use to subtract \(3\) from \(7\) is
\[7-3 \nonumber\]
We read \(7 − 3\) as seven minus three and the result is the difference of seven and three.
To describe subtraction, we can use symbols and words.
| Operation | Notation | Expression | Read as | Result |
|---|---|---|---|---|
| Subtraction | - | 7 - 3 | seven minus three | the difference of 7 and 3 |
Translate from math notation to words:
- \(8 − 1\)
- \(26 − 14\)
Solution
- We read this as eight minus one. The result is the difference of eight and one.
- We read this as twenty-six minus fourteen. The result is the difference of twenty-six and fourteen.
Translate from math notation to words:
- \(12 − 4\)
- \(29 − 11\)
- Answer a
-
twelve minus four; the difference of twelve and four
- Answer b
-
twenty-nine minus eleven; the difference of twenty-nine and eleven
Translate from math notation to words:
- \(11 − 2\)
- \(29 − 12\)
- Answer a
-
eleven minus two; the difference of eleven and two
- Answer b
-
twenty-nine minus twelve; the difference of twenty-nine and twelve
Model Subtraction of Whole Numbers
A model can help us visualize the process of subtraction much as it did with addition. Again, we will use base-\(10\) blocks. Remember a block represents \(1\) and a rod represents \(10\). Let’s start by modeling the subtraction expression we just considered, \(7 − 3\).
| We start by modeling the first number, 7. |  |
| Now take away the second number, 3. We'll circle 3 blocks to show that we are taking them away. |  |
| Count the number of blocks remaining. |  |
| There are 4 ones blocks left. | We have shown that 7 − 3 = 4. |
Model the subtraction: \(8 − 2\).
Solution
| 8 − 2 means the difference of 8 and 2. | |
| Model the first, 8. |  |
| Take away the second number, 2. |  |
| Count the number of blocks remaining. |  |
| There are 6 ones blocks left. | We have shown that 8 − 2 = 6 . |
Model: \(9 − 6\).
- Answer
-
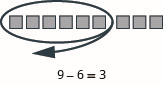
Model: \(6 − 1\).
- Answer
-
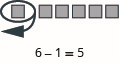
Model the subtraction: \(13 − 8\).
Solution
| Model the first number, 13. We use 1 ten and 3 ones. |  |
| Take away the second number, 8. However, there are not 8 ones, so we will exchange the 1 ten for 10 ones. |  |
| Now we can take away 8 ones. |  |
| Count the blocks remaining. |  |
| There are five ones left. | We have shown that 13 − 8 = 5. |
As we did with addition, we can describe the models as ones blocks and tens rods, or we can simply say ones and tens.
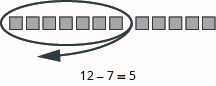
Model the subtraction: \(12 − 7\).
- Answer
-
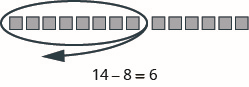
Model the subtraction: \(14 − 8\).
- Answer
-
Model the subtraction: \(43 − 26\).
Solution
Because \(43 − 26\) means \(43\) take away \(26\), we begin by modeling the \(43\).

Now, we need to take away \(26\), which is \(2\) tens and \(6\) ones. We cannot take away \(6\) ones from \(3\) ones. So, we exchange \(1\) ten for \(10\) ones.

Now we can take away \(2\) tens and \(6\) ones.
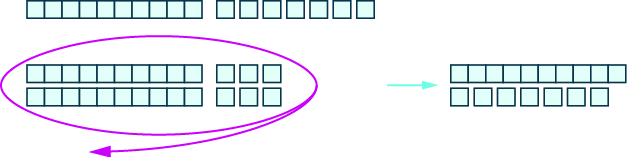
Count the number of blocks remaining. There is \(1\) ten and \(7\) ones, which is \(17\).
\[43 − 26 = 17 \nonumber\]
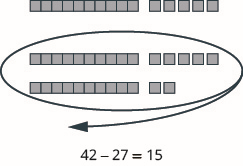
Model the subtraction: \(42 − 27\).
- Answer
-
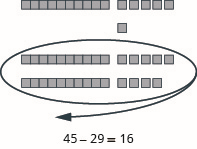
Model the subtraction: \(45 − 29\).
- Answer
-
Subtract Whole Numbers
Addition and subtraction are inverse operations. Addition undoes subtraction, and subtraction undoes addition. We know \(7 − 3 = 4\) because \(4 + 3 = 7\). Knowing all the addition number facts will help with subtraction. Then we can check subtraction by adding. In the examples above, our subtractions can be checked by addition.
\[\begin{split} 7 − 3 = 4 \qquad &\text{because} \qquad 4 + 3 = 7 \\ 13 − 8 = 5 \qquad &\text{because} \qquad 5 + 8 = 13 \\ 43 − 26 = 17 \qquad &\text{because} \qquad 17 + 26 = 43 \end{split}\]
Subtract and then check by adding:
- \(9 − 7\)
- \(8 − 3\)
Solution
| 9 - 7 | |
| Subtract 7 from 9. | 2 |
| Check with addition. 2 + 7 = 9 ✓ |
| 8 - 3 | |
| Subtract 3 from 8. | 5 |
| Check with addition. 5 + 3 = 8 ✓ |
Subtract and then check by adding: \(7 − 0\)
- Answer
-
\(7-0=7; 7+0=7\)
Subtract and then check by adding: \(6 − 2\)
- Answer
-
\(6-2=4; 2+4=6\)
To subtract numbers with more than one digit, it is usually easier to write the numbers vertically in columns just as we did for addition. Align the digits by place value, and then subtract each column starting with the ones and then working to the left.
Subtract and then check by adding: \(89 − 61\).
Solution
| Write the numbers so the ones and tens digits line up vertically. | 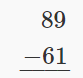 |
|
Subtract the digits in each place value. Subtract the ones: 9 - 1 = 8 Subtract the tens: 8 - 6 = 2 |
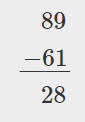 |
| Check using addition. | 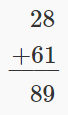 |
Our answer is correct.
Subtract and then check by adding: \(86 − 54\).
- Answer
-
\(86-54=32\) because \(54+32=86\)
Subtract and then check by adding: \(99 − 74\).
- Answer
-
\(99-74=25\) because \(74+25=99\)
When we modeled subtracting \(26\) from \(43\), we exchanged \(1\) ten for \(10\) ones. When we do this without the model, we say we borrow \(1\) from the tens place and add \(10\) to the ones place.
Step 1. Write the numbers so each place value lines up vertically
Step 2. Subtract the digits in each place value. Work from right to left starting with the ones place. If the digit on top is less than the digit below, borrow as needed.
Step 3. Continue subtracting each place value from right to left, borrowing if needed.
Step 4. Check by adding.
Subtract: \(43 − 26\).
Solution
| Write the numbers so each place value lines up vertically | 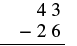 |
| Subtract the ones. We cannot subtract 6 from 3, so we borrow 1 ten. This makes 3 tens and 13 ones. We write these numbers above each place and cross out the original digits. | 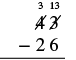 |
| Now we can subtract the ones. 13 − 6 = 7. We write the 7 in the ones place in the difference. | 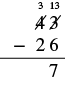 |
| Now we subtract the tens. 3 − 2 = 1. We write the 1 in the tens place in the difference. | 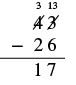 |
| Check by adding. | 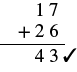 |
Our answer is correct.
Subtract and then check by adding: \(93 − 58\).
- Answer
-
\(93-58=35\) because \(58+35=93\)
Subtract and then check by adding: \(81 − 39\).
- Answer
-
\(81-39=42\) because \(42+39=81\)
Subtract and then check by adding: \(207 − 64\).
Solution
| Write the numbers so each place value lines up vertically | 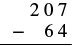 |
| Subtract the ones. 7 − 4 = 3. Write the 3 in the ones place in the difference. Write the 3 in the ones place in the difference. | 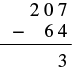 |
| Subtract the tens. We cannot subtract 6 from 0 so we borrow 1 hundred and add 10 tens to the 0 tens we had. This makes a total of 10 tens. We write 10 above the tens place and cross out the 0. Then we cross out the 2 in the hundreds place and write 1 above it. | 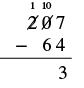 |
| Now we subtract the tens. 10 − 6 = 4. We write the 4 in the tens place in the difference. | 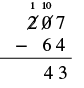 |
| Finally, subtract the hundreds. There is no digit in the hundreds place in the bottom number so we can imagine a 0 in that place. Since 1 − 0 = 1, we write 1 in the hundreds place in the difference. | 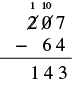 |
| Check by adding. | 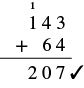 |
Our answer is correct.
Subtract and then check by adding: \(439 − 52\).
- Answer
-
\(439-52=387\) because \(387+52=439\)
Subtract and then check by adding: \(318 − 75\).
- Answer
-
\(318-75=243\) because \(243+75=318\)
Subtract and then check by adding: \(910 − 586\).
Solution
| Write the numbers so each place value lines up vertically. | 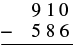 |
| Subtract the ones. We cannot subtract 6 from 0, so we borrow 1 ten and add 10 ones to the 10 ones we had. This makes 10 ones. We write a 0 above the tens place and cross out the 1. We write the 10 above the ones place and cross out the 0. Now we can subtract the ones. 10 − 6 = 4. | 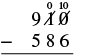 |
| Write the 4 in the ones place of the difference. | 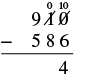 |
| Subtract the tens. We cannot subtract 8 from 0, so we borrow 1 hundred and add 10 tens to the 0 tens we had, which gives us 10 tens. Write 8 above the hundreds place and cross out the 9. Write 10 above the tens place. | 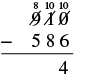 |
| Now we can subtract the tens. 10 − 8 = 2. | 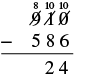 |
| Subtract the hundreds place. 8 − 5 = 3. Write the 3 in the hundreds place in the difference. | 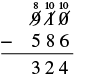 |
| Check by adding. | 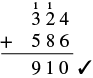 |
Our answer is correct.
Subtract and then check by adding: \(832 − 376\).
- Answer
-
\(832-376=456\) because \(456+376=832\)
Subtract and then check by adding: \(847 − 578\).
- Answer
-
\(847-578=269\) because \(578+269=847\)
Subtract and then check by adding: \(2,162 − 479\).
Solution
| Write the numbers so each place values line up vertically. | 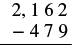 |
| Subtract the ones. Since we cannot subtract 9 from 2, borrow 1 ten and add 10 ones to the 2 ones to make 12 ones. Write 5 above the tens place and cross out the 6. Write 12 above the ones place and cross out the 2. | 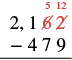 |
| Now we can subtract the ones. | 12 - 9 = 3 |
| Write 3 in the ones place in the difference | 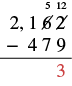 |
| Subtract the tens. Since we cannot subtract 7 from 5, borrow 1 hundred and add 10 tens to the 5 tens to make 15 tens. Write 0 above the hundreds place and cross out the 1. Write 15 above the tens place. | 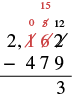 |
| Now we can subtract the tens. | 15 - 7 = 8 |
| Write 8 in the tens place in the difference. | 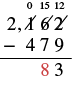 |
| Now we can subtract the hundreds. | 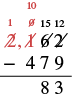 |
| Write 6 in the hundreds place in the difference | 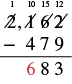 |
| Subtract the thousands. There is no digit in the thousands place of the bottom number, so we imagine a 0. 1 − 0 = 1. Write 1 in the thousands place of the difference. | 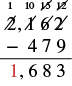 |
| Check by adding. | 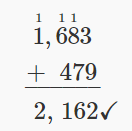 |
Our answer is correct.
Subtract and then check by adding: \(4,585 − 697\).
- Answer
-
\(4,585-697=3,888\) because \(3,888+697=4,585\)
Subtract and then check by adding: \(5,637 − 899\).
- Answer
-
\(5,637-899=4,738\) because \(4,738+899=5,637\)
Contributors and Attributions
- Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.


