1.8: Multiply Whole Numbers (Part 2)

Last updated
Save as PDF

Page ID: 5772

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Translate Word Phrases to Math Notation

Earlier in this section, we translated math notation into words. Now we’ll reverse the process and translate word phrases into math notation. Some of the words that indicate multiplication are given in Table $\PageIndex{3}$.

Table $\PageIndex{3}$
Operation	Word Phrase	Example	Expression
Multiplication	times	3 times 8	3 × 8, 3 • 8, (3)(8),
	product	the product of 3 and 8	(3)8, or 3(8)
	twice	twice 4	2 • 4

Example $\PageIndex{12}$: Translate and simplify

Translate and simplify: the product of $12$ and $27$.

Solution

The word product tells us to multiply. The words of $12$ and $27$ tell us the two factors.

	the product of 12 and 27
Translate.	12 • 27
Multiply.	324

exercise $\PageIndex{23}$

Translate and simplify the product of $13$ and $28$.

Answer: $13 · 28$; $364$

exercise $\PageIndex{24}$

Translate and simplify the product of $47$ and $14$.

Answer: $47 · 14$; $658$

Example $\PageIndex{13}$: translate and simplify

Translate and simplify: twice two hundred eleven.

Solution

The word twice tells us to multiply by $2$.

	twice two hundred eleven
Translate.	2(211)
Multiply.	422

exercise $\PageIndex{25}$

Translate and simplify: twice one hundred sixty-seven.

Answer: $2(167)$; $334$

exercise $\PageIndex{26}$

Translate and simplify: twice two hundred fifty-eight.

Answer: $2(258)$; $516$

Multiply Whole Numbers in Applications

We will use the same strategy we used previously to solve applications of multiplication. First, we need to determine what we are looking for. Then we write a phrase that gives the information to find it. We then translate the phrase into math notation and simplify to get the answer. Finally, we write a sentence to answer the question.

Example $\PageIndex{14}$: multiply

Humberto bought $4$ sheets of stamps. Each sheet had $20$ stamps. How many stamps did Humberto buy?

Solution

We are asked to find the total number of stamps.

Write a phrase for the total.	the product of 4 and 20
Translate to math notation.	4 • 20
Multiply.	$CNX_BMath_Figure_01_04_021_img-01.png$
Write a sentence to answer the question.	Humberto bought 80 stamps.

exercise $\PageIndex{27}$

Valia donated water for the snack bar at her son’s baseball game. She brought $6$ cases of water bottles. Each case had $24$ water bottles. How many water bottles did Valia donate?

Answer: Valia donated $144$ water bottles.

exercise $\PageIndex{28}$

Vanessa brought $8$ packs of hot dogs to a family reunion. Each pack has $10$ hot dogs. How many hot dogs did Vanessa bring?

Answer: Vanessa bought $80$ hot dogs.

Example $\PageIndex{15}$: multiply

When Rena cooks rice, she uses twice as much water as rice. How much water does she need to cook $4$ cups of rice?

Solution

We are asked to find how much water Rena needs.

Write as a phrase.	twice as much as 4 cups
Translate to math notation.	2 • 4
Multiply to simplify.	8
Write a sentence to answer the question.	Rena needs 8 cups of water for cups of rice.

exercise $\PageIndex{29}$

Erin is planning her flower garden. She wants to plant twice as many dahlias as sunflowers. If she plants $14$ sunflowers, how many dahlias does she need?

Answer: Erin needs $28$ dahlias.

exercise $\PageIndex{30}$

A college choir has twice as many women as men. There are $18$ men in the choir. How many women are in the choir?

Answer: There are $36$ women in the choir.

Example $\PageIndex{16}$: multiply

Van is planning to build a patio. He will have $8$ rows of tiles, with $14$ tiles in each row. How many tiles does he need for the patio?

Solution

We are asked to find the total number of tiles.

Write as a phrase.	the product of 8 and 14
Translate to math notation.	8 • 14
Multiply to simplify.	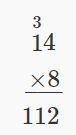$Math_1.4_004.png$
Write a sentence to answer the question.	Van needs 112 tiles for his patio.

exercise $\PageIndex{31}$

Jane is tiling her living room floor. She will need $16$ rows of tile, with $20$ tiles in each row. How many tiles does she need for the living room floor?

Answer: Jane needs $320$ tiles.

exercise $\PageIndex{32}$

Yousef is putting shingles on his garage roof. He will need $24$ rows of shingles, with $45$ shingles in each row. How many shingles does he need for the garage roof?

Answer: Yousef needs $1,080$ tiles.

If we want to know the size of a wall that needs to be painted or a floor that needs to be carpeted, we will need to find its area. The area is a measure of the amount of surface that is covered by the shape. Area is measured in square units. We often use square inches, square feet, square centimeters, or square miles to measure area. A square centimeter is a square that is one centimeter (cm.) on a side. A square inch is a square that is one inch on each side, and so on.

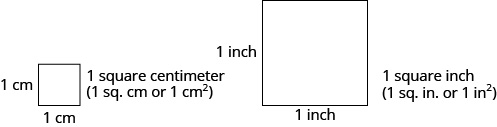
$An image of two squares, one larger than the other. The smaller square is 1 centimeter by 1 centimeter and has the label “1 square centimeter”. The larger square is 1 inch by 1 inch and has the label “1 square inch”.$

Figure $\PageIndex{2}$

For a rectangular figure, the area is the product of the length and the width. Figure $\PageIndex{3}$ shows a rectangular rug with a length of $2$ feet and a width of $3$ feet. Each square is $1$ foot wide by $1$ foot long, or $1$ square foot. The rug is made of $6$ squares. The area of the rug is $6$ square feet.

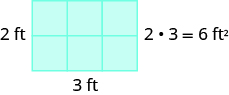
$An image of a rectangle containing 6 blocks, 2 feet tall and 3 feet wide. This image has the label “2 times 3 = 6 feet squared”.$

Figure $\PageIndex{3}$: The area of a rectangle is the product of its length and its width, or 6 square feet.

Example $\PageIndex{17}$: area

Jen’s kitchen ceiling is a rectangle that measures $9$ feet long by $12$ feet wide. What is the area of Jen’s kitchen ceiling?

Solution

We are asked to find the area of the kitchen ceiling.

Write as a phrase.	the product of 9 and 12
Translate to math notation.	9 • 12
Multiply to simplify.	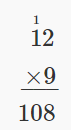$Math_1.4_005.png$
Write a sentence to answer the question.	The area of Jen's kitchen ceiling is 108 square feet.

exercise $\PageIndex{33}$

Zoila bought a rectangular rug. The rug is $8$ feet long by $5$ feet wide. What is the area of the rug?

Answer: The area of the rug is $40$ square feet.

exercise $\PageIndex{34}$

Rene’s driveway is a rectangle $45$ feet long by $20$ feet wide. What is the area of the driveway?

Answer: The area of the driveway is $900$ square feet

Access Additional Online Resources

Key Concepts

Operation	Notation	Expression	Read as	Result

Multiplication Property of Zero
- The product of any number and $0$ is $0$.
Identity Property of Multiplication
- The product of any number and $1$ is the number.
Commutative Property of Multiplication
- Changing the order of the factors does not change their product.
Multiply two whole numbers to find the product.
- Write the numbers so each place value lines up vertically.
- Multiply the digits in each place value.
- Work from right to left, starting with the ones place in the bottom number.
- Multiply the bottom number by the ones digit in the top number, then by the tens digit, and so on.
- If a product in a place value is more than $9$, carry to the next place value.
- Write the partial products, lining up the digits in the place values with the numbers above. Repeat for the tens place in the bottom number, the hundreds place, and so on.
- Insert a zero as a placeholder with each additional partial product.
- Add the partial products.

Glossary

product: The product is the result of multiplying two or more numbers.

Practice Makes Perfect

Use Multiplication Notation

In the following exercises, translate from math notation to words.

4 × 7
8 × 6
5 • 12
3 • 9
(10)(25)
(20)(15)
42(33)
39(64)

Model Multiplication of Whole Numbers

In the following exercises, model the multiplication.

3 × 6
4 × 5
5 × 9
3 × 9

Multiply Whole Numbers

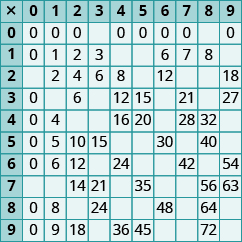
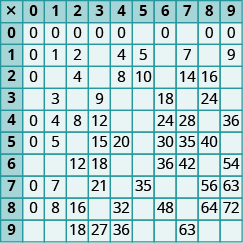
In the following exercises, fill in the missing values in each chart.

$An image of a table with 11 columns and 11 rows. The cells in the first row and first column are shaded darker than the other cells. The first column has the values “x; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9”. The second column has the values “0; 0; 0; null; 0; 0; 0; 0; null; 0; 0”. The third column has the values “1; 0; 1; 2; null; 4; 5; 6; null; 8; 9”. The fourth column has the values “2; 0; 2; 4; 6; null; 10; 12; 14; null; 18”. The fifth column has the values “3; null; 3; 6; null; null; 15; null; 21; 24; null”. The sixth column has the values “4; 0; null; 8; 12; 16; null; 24; null; null; 36”. The seventh column has the values “5; 0; null; null; 15; 20; null; null; 35; null; 45”. The eighth column has the values “6; 0; 6; 12; null; null; 30; null; null; 48; null”. The ninth column has the values “7; 0; 7; null; 21; 28; null; 42; null; null; null”. The tenth column has the values “8; null; 8; null; null; 32; 40; null; 56; 64; 72”. The eleventh column has the values “9; 0; null; 18; 27; null, null; 54; 63; null; null”.$
$An image of a table with 11 columns and 11 rows. The cells in the first row and first column are shaded darker than the other cells. The first column has the values “x; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9”. The second column has the values “0; 0; 0; 0 pink; 0; 0; 0; 0; 0; 0; 0”. The third column has the values “1; 0; 1; 2; 3; 4; 5; 6; 7; 8; 9”. The fourth column has the values “2; 0; 2; 4; 6; 8; 10; 12; 14; 16; 18”. The fifth column has the values “3; 0; 3; 6; 9; 12; 15; 18; 21; 24; 27”. The sixth column has the values “4; 0; 4; 8; 12; 16; 20; 24; 28; 32; 36”. The seventh column has the values “5; 0; 5; 10; 15; 20; 25; 30; 35; 40; 45”. The eighth column has the values “6; 0; 6; 12; 18; 24; 30; 36; 42; 48; 54”. The ninth column has the values “7; 0; 7; 14; 21; 28; 35; 42; 49; 56; 63”. The tenth column has the values “8; 0; 8; 16; 24; 32; 40; 48; 56; 64; 72”. The eleventh column has the values “9; 0; 9; 18; 27; 36, 45; 54; 63; 72; 81”.$
$An image of a table with 8 columns and 7 rows. The cells in the first row and first column are shaded darker than the other cells. The cells not in the first row or column are all null. The first column has the values “x; 4; 5; 6; 7; 8; 9”. The first row has the values “x; 3; 4; 5; 6; 7; 8; 9”.$
$PROD: An image of a table with 7 columns and 8 rows. The cells in the first row and first column are shaded darker than the other cells. The cells not in the first row or column are all null. The first column has the values “x; 3; 4; 5; 6; 7; 8; 9”. The first row has the values “x; 4; 5; 6; 7; 8; 9”.$
$An image of a table with 8 columns and 5 rows. The cells in the first row and first column are shaded darker than the other cells. The cells not in the first row or column are all null. The first row has the values “x; 3; 4; 5; 6; 7; 8; 9”. The first column has the values “x; 6; 7; 8; 9”.$
$An image of a table with 5 columns and 8 rows. The cells in the first row and first column are shaded darker than the other cells. The cells not in the first row or column are all null. The first column has the values “x; 3; 4; 5; 6; 7; 8; 9”. The first row has the values “x; 6; 7; 8; 9”.$
$PROD: An image of a table with 6 columns and 6 rows. The cells in the first row and first column are shaded darker than the other cells. The cells not in the first row or column are all null. The first column has the values “x; 5; 6; 7; 8; 9”. The first row has the values “x; 5; 6; 7; 8; 9”.$
$An image of a table with 6 columns and 6 rows. The cells in the first row and first column are shaded darker than the other cells. The cells not in the first row or column are all null. The first column has the values “x; 5; 6; 7; 8; 9”. The first row has the values “x; 5; 6; 7; 8; 9”.$

In the following exercises, multiply.

0 • 15
0 • 41
(99)0
(77)0
1 • 43
1 • 34
(28)1
(65)1
1(240,055)
1(189,206)
(a) 7 • 6 (b) 6 • 7
(a) 8 × 9 (b) 9 × 8
(79)(5)
(58)(4)
275 • 6
638 • 5
3,421 × 7
9,143 × 3
52(38)
37(45)
96 • 73
89 • 56
27 × 85
53 × 98
23 • 10
19 • 10
(100)(36)
(100)(25)
1,000(88)
1,000(46)
50 × 1,000,000
30 × 1,000,000
247 × 139
156 × 328
586(721)
472(855)
915 • 879
968 • 926
(104)(256)
(103)(497)
348(705)
485(602)
2,719 × 543
3,581 × 724

Translate Word Phrases to Math Notation

In the following exercises, translate and simplify.

the product of 18 and 33
the product of 15 and 22
fifty-one times sixty-seven
forty-eight times seventy-one
twice 249
twice 589
ten times three hundred seventy-five
ten times two hundred fifty-five

Mixed Practice

In the following exercises, simplify.

38 × 37
86 × 29
415 − 267
341 − 285
6,251 + 4,749
3,816 + 8,184
(56)(204)
(77)(801)
947 • 0
947 + 0
15,382 + 1
15,382 • 1

In the following exercises, translate and simplify.

the difference of 50 and 18
the difference of 90 and 66
twice 35
twice 140
20 more than 980
65 more than 325
the product of 12 and 875
the product of 15 and 905
subtract 74 from 89
subtract 45 from 99
the sum of 3,075 and 950
the sum of 6,308 and 724
366 less than 814
388 less than 925

Multiply Whole Numbers in Applications

In the following exercises, solve.

Party supplies Tim brought 9 six-packs of soda to a club party. How many cans of soda did Tim bring?
Sewing Kanisha is making a quilt. She bought 6 cards of buttons. Each card had four buttons on it. How many buttons did Kanisha buy?
Field trip Seven school busses let off their students in front of a museum in Washington, DC. Each school bus had 44 students. How many students were there?
Gardening Kathryn bought 8 flats of impatiens for her flower bed. Each flat has 24 flowers. How many flowers did Kathryn buy?
Charity Rey donated 15 twelve-packs of t-shirts to a homeless shelter. How many t-shirts did he donate?
School There are 28 classrooms at Anna C. Scott elementary school. Each classroom has 26 student desks. What is the total number of student desks?
Recipe Stephanie is making punch for a party. The recipe calls for twice as much fruit juice as club soda. If she uses 10 cups of club soda, how much fruit juice should she use?
Gardening Hiroko is putting in a vegetable garden. He wants to have twice as many lettuce plants as tomato plants. If he buys 12 tomato plants, how many lettuce plants should he get?
Government The United States Senate has twice as many senators as there are states in the United States. There are 50 states. How many senators are there in the United States Senate?
Recipe Andrea is making potato salad for a buffet luncheon. The recipe says the number of servings of potato salad will be twice the number of pounds of potatoes. If she buys 30 pounds of potatoes, how many servings of potato salad will there be?
Painting Jane is painting one wall of her living room. The wall is rectangular, 13 feet wide by 9 feet high. What is the area of the wall?
Home décor Shawnte bought a rug for the hall of her apartment. The rug is 3 feet wide by 18 feet long. What is the area of the rug?
Room size The meeting room in a senior center is rectangular, with length 42 feet and width 34 feet. What is the area of the meeting room?
Gardening June has a vegetable garden in her yard. The garden is rectangular, with length 23 feet and width 28 feet. What is the area of the garden?
NCAA basketball According to NCAA regulations, the dimensions of a rectangular basketball court must be 94 feet by 50 feet. What is the area of the basketball court?
NCAA football According to NCAA regulations, the dimensions of a rectangular football field must be 360 feet by 160 feet. What is the area of the football field?

Everyday Math

Stock market Javier owns 300 shares of stock in one company. On Tuesday, the stock price rose $12 per share. How much money did Javier’s portfolio gain?
Salary Carlton got a $200 raise in each paycheck. He gets paid 24 times a year. How much higher is his new annual salary?

Writing Exercises

How confident do you feel about your knowledge of the multiplication facts? If you are not fully confident, what will you do to improve your skills?
How have you used models to help you learn the multiplication facts?

Self Check

(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

$CNX_BMath_Figure_AppB_005.jpg$

(b) On a scale of 1–10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

Contributors and Attributions

Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (formerly of Santa Ana College). This content produced by OpenStax and is licensed under a Creative Commons Attribution License 4.0 license.

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{12}\): Translate and simplify

exercise \(\PageIndex{23}\)

exercise \(\PageIndex{24}\)

Example \(\PageIndex{13}\): translate and simplify

exercise \(\PageIndex{25}\)

exercise \(\PageIndex{26}\)

Example \(\PageIndex{14}\): multiply

exercise \(\PageIndex{27}\)

exercise \(\PageIndex{28}\)

Example \(\PageIndex{15}\): multiply

exercise \(\PageIndex{29}\)

exercise \(\PageIndex{30}\)

Example \(\PageIndex{16}\): multiply

exercise \(\PageIndex{31}\)

exercise \(\PageIndex{32}\)

Example \(\PageIndex{17}\): area

exercise \(\PageIndex{33}\)

exercise \(\PageIndex{34}\)