3.1: Prelude to the Integral

Last updated
Save as PDF

Page ID: 79379

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The previous chapters dealt with Differential Calculus. We started with the simple geometrical idea of the slope of a tangent line to a curve, developed it into a combination of theory about derivatives and their properties, techniques for calculating derivatives, and applications of derivatives. This chapter deals with Integral Calculus and starts with the simple geometric idea of area. This idea will be developed into another combination of theory, techniques, and applications.

PreCalculus Idea – The Area of a Rectangle

If you look on the inside cover of nearly any traditional math book, you will find a bunch of area and volume formulas – the area of a square, the area of a trapezoid, the volume of a right circular cone, and so on. Some of these formulas are pretty complicated. But you still won't find a formula for the area of a jigsaw puzzle piece or the volume of an egg. There are lots of things for which there is no formula. Yet we might still want to find their areas.

One reason areas are so useful is that they can represent quantities other than simple geometric shapes. If the units for each side of the rectangle are meters, then the area will have the units \(meters \cdot meters = square \ meters = \text{m}^2\). But if the units of the base of a rectangle are hours and the units of the height are miles/hour, then the units of the area of the rectangle are \(hours \cdot (miles/hour) = miles\), a measure of distance. Similarly, if the base units are centimeters and the height units are grams, then the area units are gram-centimeters, a measure of work.

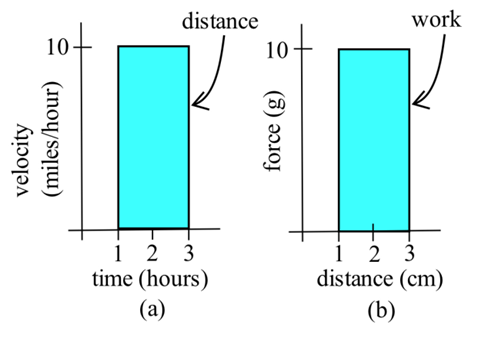
The basic shape we will use is the rectangle; the area of a rectangle is base\( \cdot \)height. You should also know the area formulas for triangles, \( A=\frac{1}{2}bh \), and for circles, \( A=\pi r^2 \).