1.4: Functions
- Page ID
- 442
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)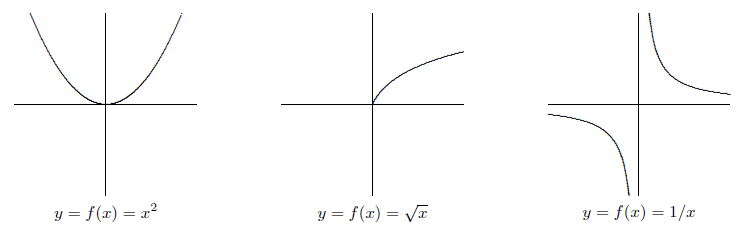
For example, the square-root function \(y=f(x)=\sqrt{x}\) is the rule which says, given an \(x\)-value, take the nonnegative number whose square is \(x\). This rule only makes sense if \(x\) is positive or zero. We say that the domain of this function is \(x\ge 0\), or more formally \[\{x\in R\mid x\ge 0\} \nonumber \]. Alternately, we can use interval notation, and write that the domain is \(0,\infty)\). (In interval notation, square brackets mean that the endpoint is included, and a parenthesis means that the endpoint is not included.) The fact that the domain of \(y=\sqrt{x}\) is \([0,\infty)\) means that in the graph of this function (see figure 1.3.1) we have points \((x,y)\) only above \(x\)-values on the right side of the \(x\)-axis.
Another example of a function whose domain is not the entire \(x\)-axis is: \(y=f(x)=1/x\), the reciprocal function. We cannot substitute \(x=0\) in this formula. The function makes sense, however, for any nonzero \(x\), so we take the domain to be:
\[\{x\in R\mid x\ne 0.\} \nonumber \]
The graph of this function does not have any point \((x,y)\) with \(x=0\). As \(x\) gets close to 0 from either side, the graph goes off toward infinity. We call the vertical line \(x=0\) an asymptote.
To summarize, two reasons why certain (x\)-values are excluded from the domain of a function are that (i) we cannot divide by zero, and (ii) we cannot take the square root of a negative number. We will encounter some other ways in which functions might be undefined later.
Another reason why the domain of a function might be restricted is that in a given situation the \(x\)-values outside of some range might have no practical meaning. For example, if \(y\) is the area of a square of side \(x\), then we can write \(y=f(x)=x^2\). In a purely mathematical context the domain of the function \(y=x^2\) is all of \(R\). But in the story-problem context of finding areas of squares, we restrict the domain to positive values of \(x\), because a square with negative or zero side makes no sense.
In a problem in pure mathematics, we usually take the domain to be all values of \(x\) at which the formulas can be evaluated. But in a story problem there might be further restrictions on the domain because only certain values of \(x\) are of interest or make practical sense.
In a story problem, often letters different from \(x\) and \(y\) are used. For example, the volume \(V\) of a sphere is a function of the radius \(r\), given by the formula \(V=f(r)=\frac4/3\pi r^3\). Also, letters different from \(f\) may be used. For example, if \(y\) is the velocity of something at time \(t\), we may write \(y=v(t)\) with the letter \(v\) (instead of \(f\)) standing for the velocity function (and \(t\) playing the role of \(x\)).
The letter playing the role of \(x\) is called the independent variable, and the letter playing the role of \(y\) is called the dependent variable (because its value "depends on'' the value of the independent variable). In story problems, when one has to translate from English into mathematics, a crucial step is to determine what letters stand for variables. If only words and no letters are given, then we have to decide which letters to use. Some letters are traditional. For example, almost always, \(t\) stands for time.
First method. Factor \(4x-x^2\) as \(x(4-x)\). The product of two numbers is positive when either both are positive or both are negative, i.e., if either \(x>0\) and \(4-x>0\), or else \(x < 0\) and \(4-x < 0\). The latter alternative is impossible, since if \(x\) is negative, then \(4-x\) is greater than 4, and so cannot be negative. As for the first alternative, the condition \(4-x>0\) can be rewritten (adding \(x\) to both sides) as \(4>x\), so we need: \(x>0\) and \(4>x\) (this is sometimes combined in the form \(4>x>0\), or, equivalently, \(0 < x < 4\)). In interval notation, this says that the domain is the interval \((0,4)\). Second method. Write \(4x-x^2\) as \(-(x^2-4x)\), and then complete the square, obtaining \[-\Bigl((x-2)^2-4\Bigr)=4-(x-2)^2 \nonumber \]. For this to be positive we need \((x-2)^2 < 4\), which means that \(x-2\) must be less than 2 and greater than \(-2\): \(-2 < x-2 < 2\). Adding 2 to everything gives \(0 < x < 4\). Both of these methods are equally correct; you may use either in a problem of this type.
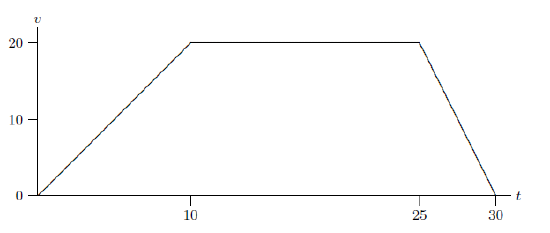
Not all functions are given by formulas at all. A function can be given by an experimentally determined table of values, or by a description other than a formula. For example, the population \(y\) of the U.S. is a function of the time \(t\): we can write \(y=f(t)\). This is a perfectly good function---we could graph it (up to the present) if we had data for various \(t\)---but we can't find an algebraic formula for it.