10.3E: Exercises for Section 10.3

Taylor Polynomials

In exercises 1 - 8, find the Taylor polynomials of degree two approximating the given function centered at the given point.

1) $f(x)=1+x+x^2$ at $a=1$

2) $f(x)=1+x+x^2$ at $a=−1$

Answer

$f(−1)=1;\;f′(−1)=−1;\;f''(−1)=2;\quad p_2(x)=1−(x+1)+(x+1)^2$

3) $f(x)=\cos(2x)$ at $a=π$

4) $f(x)=\sin(2x)$ at $a=\frac{π}{2}$

Answer

$f′(x)=2\cos(2x);\;f''(x)=−4\sin(2x);\quad p_2(x)=−2(x−\frac{π}{2})$

5) $f(x)=\sqrt{x}$ at $a=4$

6) $f(x)=\ln x$ at $a=1$

Answer

$f′(x)=\dfrac{1}{x};\; f''(x)=−\dfrac{1}{x^2};\quad p_2(x)=0+(x−1)−\frac{1}{2}(x−1)^2$

7) $f(x)=\dfrac{1}{x}$ at $a=1$

8) $f(x)=e^x$ at $a=1$

Answer

$p_2(x)=e+e(x−1)+\dfrac{e}{2}(x−1)^2$

Taylor Remainder Theorem

In exercises 9 - 14, verify that the given choice of $n$ in the remainder estimate $|R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}$, where $M$ is the maximum value of $∣f^{(n+1)}(z)∣$ on the interval between $a$ and the indicated point, yields $|R_n|≤\frac{1}{1000}$. Find the value of the Taylor polynomial $p_n$ of $f$ at the indicated point.

9) [T] $\sqrt{10};\; a=9,\; n=3$

10) [T] $(28)^{1/3};\; a=27,\; n=1$

Answer

$\dfrac{d^2}{dx^2}x^{1/3}=−\dfrac{2}{9x^{5/3}}≥−0.00092…$ when $x≥28$ so the remainder estimate applies to the linear approximation $x^{1/3}≈p_1(27)=3+\dfrac{x−27}{27}$, which gives $(28)^{1/3}≈3+\frac{1}{27}=3.\bar{037}$, while $(28)^{1/3}≈3.03658.$

11) [T] $\sin(6);\; a=2π,\; n=5$

12) [T] $e^2; \; a=0,\; n=9$

Answer

Using the estimate $\dfrac{2^{10}}{10!}<0.000283$ we can use the Taylor expansion of order 9 to estimate $e^x$ at $x=2$. as $e^2≈p_9(2)=1+2+\frac{2^2}{2}+\frac{2^3}{6}+⋯+\frac{2^9}{9!}=7.3887$… whereas $e^2≈7.3891.$

13) [T] $\cos(\frac{π}{5});\; a=0,\; n=4$

14) [T] $\ln(2);\; a=1,\; n=1000$

Answer

Since $\dfrac{d^n}{dx^n}(\ln x)=(−1)^{n−1}\dfrac{(n−1)!}{x^n},R_{1000}≈\frac{1}{1001}$. One has $\displaystyle p_{1000}(1)=\sum_{n=1}^{1000}\dfrac{(−1)^{n−1}}{n}≈0.6936$ whereas $\ln(2)≈0.6931⋯.$

Approximating Definite Integrals Using Taylor Series

15) Integrate the approximation $\sin t≈t−\dfrac{t^3}{6}+\dfrac{t^5}{120}−\dfrac{t^7}{5040}$ evaluated at $π$t to approximate $\displaystyle ∫^1_0\frac{\sin πt}{πt}\,dt$.

16) Integrate the approximation $e^x≈1+x+\dfrac{x^2}{2}+⋯+\dfrac{x^6}{720}$ evaluated at $−x^2$ to approximate $\displaystyle ∫^1_0e^{−x^2}\,dx.$

Answer

$\displaystyle ∫^1_0\left(1−x^2+\frac{x^4}{2}−\frac{x^6}{6}+\frac{x^8}{24}−\frac{x^{10}}{120}+\frac{x^{12}}{720}\right)\,dx =1−\frac{1^3}{3}+\frac{1^5}{10}−\frac{1^7}{42}+\frac{1^9}{9⋅24}−\frac{1^{11}}{120⋅11}+\frac{1^{13}}{720⋅13}≈0.74683$ whereas $\displaystyle ∫^1_0e^{−x^2}dx≈0.74682.$

More Taylor Remainder Theorem Problems

In exercises 17 - 20, find the smallest value of $n$ such that the remainder estimate $|R_n|≤\dfrac{M}{(n+1)!}(x−a)^{n+1}$, where $M$ is the maximum value of $∣f^{(n+1)}(z)∣$ on the interval between $a$ and the indicated point, yields $|R_n|≤\frac{1}{1000}$ on the indicated interval.

17) $f(x)=\sin x$ on $[−π,π],\; a=0$

18) $f(x)=\cos x$ on $[−\frac{π}{2},\frac{π}{2}],\; a=0$

Answer

Since $f^{(n+1)}(z)$ is $\sin z$ or $\cos z$, we have $M=1$. Since $|x−0|≤\frac{π}{2}$, we seek the smallest $n$ such that $\dfrac{π^{n+1}}{2^{n+1}(n+1)!}≤0.001$. The smallest such value is $n=7$. The remainder estimate is $R_7≤0.00092.$

19) $f(x)=e^{−2x}$ on $[−1,1],a=0$

20) $f(x)=e^{−x}$ on $[−3,3],a=0$

Answer

Since $f^{(n+1)}(z)=±e^{−z}$ one has $M=e^3$. Since $|x−0|≤3$, one seeks the smallest $n$ such that $\dfrac{3^{n+1}e^3}{(n+1)!}≤0.001$. The smallest such value is $n=14$. The remainder estimate is $R_{14}≤0.000220.$

In exercises 21 - 24, the maximum of the right-hand side of the remainder estimate $|R_1|≤\dfrac{max|f''(z)|}{2}R^2$ on $[a−R,a+R]$ occurs at $a$ or $a±R$. Estimate the maximum value of $R$ such that $\dfrac{max|f''(z)|}{2}R^2≤0.1$ on $[a−R,a+R]$ by plotting this maximum as a function of $R$.

21) [T] $e^x$ approximated by $1+x,\; a=0$

22) [T] $\sin x$ approximated by $x,\; a=0$

Answer

Since $\sin x$ is increasing for small $x$ and since $\frac{d^2}{dx^2}\left(\sin x\right)=−\sin x$, the estimate applies whenever $R^2\sin(R)≤0.2$, which applies up to $R=0.596.$

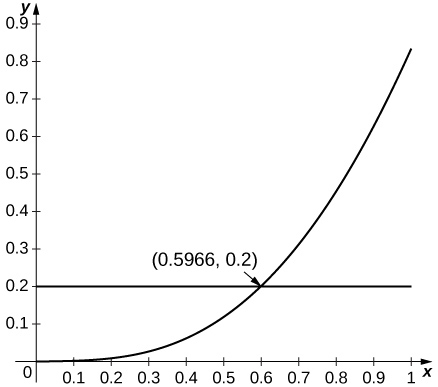
23) [T] $\ln x$ approximated by $x−1,\; a=1$

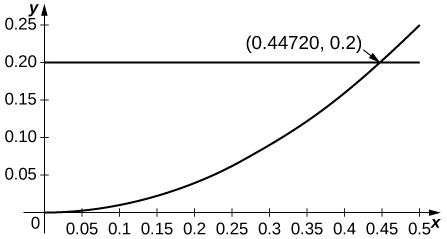
24) [T] $\cos x$ approximated by $1,\; a=0$

Answer

Since the second derivative of $\cos x$ is $−\cos x$ and since $\cos x$ is decreasing away from $x=0$, the estimate applies when $R^2\cos R≤0.2$ or $R≤0.447$.

Taylor Series

In exercises 25 - 35, find the Taylor series of the given function centered at the indicated point.

25) $f(x) = x^4$ at $a=−1$

26) $f(x) = 1+x+x^2+x^3$ at $a=−1$

Answer

$(x+1)^3−2(x+1)^2+2(x+1)$

27) $f(x) = \sin x$ at $a=π$

28) $f(x) = \cos x$ at $a=2π$

Answer

Values of derivatives are the same as for $x=0$ so $\displaystyle \cos x=\sum_{n=0}^∞(−1)^n\frac{(x−2π)^{2n}}{(2n)!}$

29) $f(x) = \sin x$ at $x=\frac{π}{2}$

30) $f(x) = \cos x$ at $x=\frac{π}{2}$

Answer

$\cos(\frac{π}{2})=0,\;−\sin(\frac{π}{2})=−1$ so $\displaystyle \cos x=\sum_{n=0}^∞(−1)^{n+1}\frac{(x−\frac{π}{2})^{2n+1}}{(2n+1)!}$, which is also $−\cos(x−\frac{π}{2})$.

31) $f(x) = e^x$ at $a=−1$

32) $f(x) = e^x$ at $a=1$

Answer

The derivatives are $f^{(n)}(1)=e,$ so $\displaystyle e^x=e\sum_{n=0}^∞\frac{(x−1)^n}{n!}.$

33) $f(x) = \dfrac{1}{(x−1)^2}$ at $a=0$ (Hint: Differentiate the Taylor Series for$\dfrac{1}{1−x}$.)

34) $f(x) = \dfrac{1}{(x−1)^3}$ at $a=0$

Answer

$\displaystyle \frac{1}{(x−1)^3}=−\frac{1}{2}\frac{d^2}{dx^2}\left(\frac{1}{1−x}\right)=−\sum_{n=0}^∞\left(\frac{(n+2)(n+1)x^n}{2}\right)$

35) $\displaystyle F(x)=∫^x_0\cos(\sqrt{t})\,dt;\quad \text{where}\; f(t)=\sum_{n=0}^∞(−1)^n\frac{t^n}{(2n)!}$ at a=0 (Note: $f$ is the Taylor series of $\cos(\sqrt{t}).)$

In exercises 36 - 44, compute the Taylor series of each function around $x=1$.

36) $f(x)=2−x$

Answer

$2−x=1−(x−1)$

37) $f(x)=x^3$

38) $f(x)=(x−2)^2$

Answer

$((x−1)−1)^2=(x−1)^2−2(x−1)+1$

39) $f(x)=\ln x$

40) $f(x)=\dfrac{1}{x}$

Answer

$\displaystyle \frac{1}{1−(1−x)}=\sum_{n=0}^∞(−1)^n(x−1)^n$

41) $f(x)=\dfrac{1}{2x−x^2}$

42) $f(x)=\dfrac{x}{4x−2x^2−1}$

Answer

$\displaystyle x\sum_{n=0}^∞2^n(1−x)^{2n}=\sum_{n=0}^∞2^n(x−1)^{2n+1}+\sum_{n=0}^∞2^n(x−1)^{2n}$

43) $f(x)=e^{−x}$

44) $f(x)=e^{2x}$

Answer

$\displaystyle e^{2x}=e^{2(x−1)+2}=e^2\sum_{n=0}^∞\frac{2^n(x−1)^n}{n!}$

Maclaurin Series

[T] In exercises 45 - 48, identify the value of $x$ such that the given series $\displaystyle \sum_{n=0}^∞a_n$ is the value of the Maclaurin series of $f(x)$ at $x$. Approximate the value of $f(x)$ using $\displaystyle S_{10}=\sum_{n=0}^{10}a_n$.

45) $\displaystyle \sum_{n=0}^∞\frac{1}{n!}$

46) $\displaystyle \sum_{n=0}^∞\frac{2^n}{n!}$

Answer

$x=e^2;\quad S_{10}=\dfrac{34,913}{4725}≈7.3889947$

47) $\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n}}{(2n)!}$

48) $\displaystyle \sum_{n=0}^∞\frac{(−1)^n(2π)^{2n+1}}{(2n+1)!}$

Answer

$\sin(2π)=0;\quad S_{10}=8.27×10^{−5}$

In exercises 49 - 52 use the functions $S_5(x)=x−\dfrac{x^3}{6}+\dfrac{x^5}{120}$ and $C_4(x)=1−\dfrac{x^2}{2}+\dfrac{x^4}{24}$ on $[−π,π]$.

49) [T] Plot $\sin^2x−(S_5(x))^2$ on $[−π,π]$. Compare the maximum difference with the square of the Taylor remainder estimate for $\sin x.$

50) [T] Plot $\cos^2x−(C_4(x))^2$ on $[−π,π]$. Compare the maximum difference with the square of the Taylor remainder estimate for $\cos x$.

Answer

The difference is small on the interior of the interval but approaches $1$ near the endpoints. The remainder estimate is $|R_4|=\frac{π^5}{120}≈2.552.$

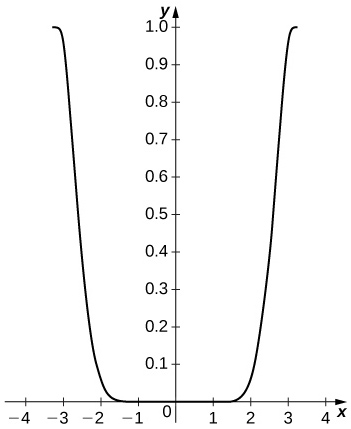
51) [T] Plot $|2S_5(x)C_4(x)−\sin(2x)|$ on $[−π,π]$.

52) [T] Compare $\dfrac{S_5(x)}{C_4(x)}$ on $[−1,1]$ to $\tan x$. Compare this with the Taylor remainder estimate for the approximation of $\tan x$ by $x+\dfrac{x^3}{3}+\dfrac{2x^5}{15}$.

Answer

The difference is on the order of $10^{−4}$ on $[−1,1]$ while the Taylor approximation error is around $0.1$ near $±1$. The top curve is a plot of $\tan^2x−\left(\dfrac{S_5(x)}{C_4(x)}\right)^2$ and the lower dashed plot shows $t^2−\left(\dfrac{S_5}{C_4}\right)^2$.

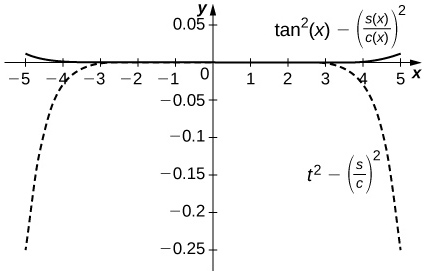
53) [T] Plot $e^x−e_4(x)$ where $e_4(x)=1+x+\dfrac{x^2}{2}+\dfrac{x^3}{6}+\dfrac{x^4}{24}$ on $[0,2]$. Compare the maximum error with the Taylor remainder estimate.

54) (Taylor approximations and root finding.) Recall that Newton’s method $x_{n+1}=x_n−\dfrac{f(x_n)}{f'(x_n)}$ approximates solutions of $f(x)=0$ near the input $x_0$.

a. If $f$ and $g$ are inverse functions, explain why a solution of $g(x)=a$ is the value $f(a)$ of $f$.

b. Let $p_N(x)$ be the $N^{\text{th}}$ degree Maclaurin polynomial of $e^x$. Use Newton’s method to approximate solutions of $p_N(x)−2=0$ for $N=4,5,6.$

c. Explain why the approximate roots of $p_N(x)−2=0$ are approximate values of $\ln(2).$

Answer

a. Answers will vary.
b. The following are the $x_n$ values after $10$ iterations of Newton’s method to approximation a root of $p_N(x)−2=0$: for $N=4,x=0.6939...;$ for $N=5,x=0.6932...;$ for $N=6,x=0.69315...;.$ (Note: $\ln(2)=0.69314...$)
c. Answers will vary.

Evaluating Limits using Taylor Series

In exercises 55 - 58, use the fact that if $\displaystyle q(x)=\sum_{n=1}^∞a_n(x−c)^n$ converges in an interval containing $c$, then $\displaystyle \lim_{x→c}q(x)=a_0$ to evaluate each limit using Taylor series.

55) $\displaystyle \lim_{x→0}\frac{\cos x−1}{x^2}$

56) $\displaystyle \lim_{x→0}\frac{\ln(1−x^2)}{x^2}$

Answer

$\dfrac{\ln(1−x^2)}{x^2}→−1$

57) $\displaystyle \lim_{x→0}\frac{e^{x^2}−x^2−1}{x^4}$

58) $\displaystyle \lim_{x→0^+}\frac{\cos(\sqrt{x})−1}{2x}$

Answer

$\displaystyle \frac{\cos(\sqrt{x})−1}{2x}≈\frac{(1−\frac{x}{2}+\frac{x^2}{4!}−⋯)−1}{2x}→−\frac{1}{4}$