3.6: Application- Center of Mass
- Page ID
- 2247
Recall from single-variable calculus that for a region \(R = {(x, y) : a ≤ x ≤ b,0 ≤ y ≤ f (x)}\) in \(\mathbb{R}^2\) that represents a thin, flat plate (Figure 3.6.1), where \(f (x)\) is a continuous function on \([a,b]\), the center of mass of \(R\) has coordinates \((\bar x, \bar y)\) given by
\[ \bar x =\dfrac{M_y}{M} \text{ and }\bar y = \dfrac{M_x}{M}\]
where
\[M_x = \int_a^b \dfrac{(f(x))^2}{2}dx,\quad M_y = \int_a^b x f (x)\,dx, \quad M=\int_a^b f (x)\,dx \label{Eq3.27}\]
assuming that \(R\) has uniform density, i.e the mass of \(R\) is uniformly distributed over the region. In this case the area \(M\) of the region is considered the mass of \(R\) (the density is constant, and taken as 1 for simplicity).
In the general case where the density of a region (or lamina) \(R\) is a continuous function \(δ = δ(x, y)\) of the coordinates \((x, y)\) of points inside \(R\) (where \(R\) can be any region in \(\mathbb{R}^2\) ) the coordinates \((\bar x,\bar y)\) of the center of mass of \(R\) are given by
\[\bar x =\dfrac{M_y}{M} \text{ and }\bar y = \dfrac{M_x}{M}\label{Eq3.28}\]
where
\[M_y = \iint\limits_R xδ(x, y)\,d A ,\quad M_x = \iint\limits_R yδ(x, y)\,d A,\quad M=\iint\limits_R δ(x, y)\,d A ,\label{Eq3.29}\]
The quantities \(M_x \text{ and }M_y\) are called the moments (or first moments) of the region \(R\) about the \(x\)-axis and \(y\)-axis, respectively. The quantity \(M\) is the mass of the region \(R\). To see this, think of taking a small rectangle inside \(R\) with dimensions \(∆x \text{ and }∆y\) close to 0. The mass of that rectangle is approximately \(δ(x_∗, y_∗)∆x∆y\), for some point \((x_∗, y_∗)\) in that rectangle. Then the mass of \(R\) is the limit of the sums of the masses of all such rectangles inside \(R\) as the diagonals of the rectangles approach 0, which is the double integral \(\iint\limits_R δ(x, y)\,d A\).
Note that the formulas in Equation \ref{Eq3.27} represent a special case when \(δ(x, y) = 1\) throughout \(R\) in the formulas in Equation \ref{Eq3.29}.
Example 3.13: Center of Mass of a 2D Region
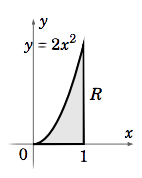
Find the center of mass of the region \(R = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 2x^2 }\), if the density function at \((x, y) \text{ is }δ(x, y) = x+ y\).
Solution:
The region \(R\) is shown in Figure 3.6.2. We have
\[\nonumber \begin{align} M&=\iint\limits_R δ(x, y)\,d A \\[4pt] \nonumber &= \int_0^1 \int_0^{2x^2}(x+ y)\,d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( xy + \dfrac{y^2}{2} \Big |_{y=0}^{y=2x^2} \right ) \,dx \\[4pt] \nonumber &=\int_0^1 (2x^3 +2x^4 )\,dx \\[4pt] \nonumber &= \dfrac{x^4}{2}+\dfrac{2x^5}{5} \Big |_0^1 = \dfrac{9}{10}\\[4pt] \end{align}\]
and
\[\nonumber \begin{split} M_x &= \iint\limits_R yδ(x, y)\,d A \\[4pt] \nonumber &=\int_0^1 \int_0^{2x^2} y(x+ y)\,d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( \dfrac{xy^2}{2}+\dfrac{y^3}{3} \Big |_{y=0}^{y=2x^2} \right )\,dx \\[4pt] \nonumber &=\int_0^1 (2x^5 + \dfrac{8x^6}{ 3} )\,dx \\[4pt] \nonumber &=\dfrac{x^6}{3} + \dfrac{8x^7}{21} \Big |_0^1 = \dfrac{5}{7} \\[4pt] \end{split} \qquad \nonumber \begin{split} M_y &= \iint\limits_R xδ(x, y)\,d A \\[4pt] \nonumber &=\int_0^1 \int_0^{2x^2} x(x+ y)\,d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( x^2y+\dfrac{xy^2}{2} \Big |_{y=0}^{y=2x^2} \right )\,dx \\[4pt] \nonumber &=\int_0^1 (2x^4 + 2x^5 )\,dx \\[4pt] &=\dfrac{2x^5}{5} + \dfrac{x^6}{3} \Big |_0^1 = \dfrac{11}{15} \\[4pt] \end{split}\]
so the center of mass \((\bar x,\bar y)\) is given by
\[\nonumber \bar x =\dfrac{M_y}{M} = \dfrac{11/15}{9/10} = \dfrac{22}{27},\quad \bar y = \dfrac{M_x}{M} = \dfrac{5/7}{9/10}=\dfrac{50}{63}\]
Note how this center of mass is a little further towards the upper corner of the region \(R\) than when the density is uniform (it is easy to use the formulas in Equation \ref{Eq3.27} to show that \((\bar x,\bar y) = \left ( \dfrac{3}{ 4} , \dfrac{3}{ 5} \right ) \) in that case). This makes sense since the density function \(δ(x, y) = x + y\) increases as \((x, y)\) approaches that upper corner, where there is quite a bit of area.
In the special case where the density function \(δ(x, y)\) is a constant function on the region \(R\), the center of mass \((\bar x,\bar y)\) is called the centroid of \(R\).
The formulas for the center of mass of a region in \(\mathbb{R}^2\) can be generalized to a solid \(S\) in \(\mathbb{R}^ 3\). Let \(S\) be a solid with a continuous mass density function \(δ(x, y, z)\) at any point \((x, y, z)\) in \(S\). Then the center of mass of \(S\) has coordinates \((\bar x,\bar y,\bar z)\), where
\[\bar x = \dfrac{M_{yz}}{M},\quad \bar y = \dfrac{M_{xz}}{M},\quad \bar z= \dfrac{M_{xy}}{M},\label{Eq3.30}\]
where
\[M_{yz} = \iiint\limits_S xδ(x, y, z)\,dV, \quad M_{xz} = \iiint\limits_S yδ(x, y, z)\,dV,\quad M_{xy} = \iiint\limits_S zδ(x, y, z)\,dV ,\label{Eq3.31}\]
\[M = \iiint\limits_S δ(x, y, z)\,dV .\label{Eq3.32}\]
In this case, \(M_{yz}, M_{xz}\text{ and }M_{x y}\) are called the moments (or first moments) of \(S\) around the \(yz\)-plane, \(xz\)-plane and \(x y\)-plane, respectively. Also, \(M\) is the mass of \(S\).
Example 3.14: Center of mass of a 3D Solid
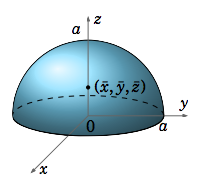
Find the center of mass of the solid \(S = {(x, y, z) : z ≥ 0, x^2 + y^2 + z^2 ≤ a^2 }\), if the density function at \((x, y, z) \text{ is }δ(x, y, z) = 1\).
Solution:
The solid \(S\) is just the upper hemisphere inside the sphere of radius \(a\) centered at the origin (see Figure 3.6.3).
So since the density function is a constant and \(S\) is symmetric about the \(z\)-axis, then it is clear that \(\bar x = 0 \text{ and }\bar y = 0\), so we need only find \(\bar z\). We have
\[\nonumber M = \iiint\limits_S δ(x, y, z)\,dV = \iiint\limits_S 1dV = \text{ Volume}(S).\]
But since the volume of \(S\) is half the volume of the sphere of radius \(a\), which we know by Example 3.12 is \(\dfrac{4\pi a}{3}\), then \(M = \dfrac{2\pi a}{3}\). And
\[\nonumber \begin{align} M_{xy} &= \iiint\limits_S zδ(x, y, z)\,dV \\[4pt] \nonumber &=\iiint\limits_S z \,dV,\text{ which in spherical coordinates is} \\[4pt] \nonumber &=\int_0^{2\pi} \int_0^{\pi /2} \int_0^a (ρ \cos{φ})ρ^2 \sin{φ}\,dρ\, dφ\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \int_0^{\pi/2} \sin{φ} \cos{φ} \left ( \int_0^a ρ^3 \,dρ \right ) \,dφ\,dθ \\[4pt] \nonumber &= \int_0^{2\pi} \int_0^{\pi/2} \dfrac{a^4}{4} \sin{φ} \cos{φ}\,dφ\,dθ \\[4pt] \nonumber M_{xy}&=\int_0^{2\pi} \int_0^{\pi/2} \dfrac{a^4}{8} \sin{2φ}\,dφ\,dθ \quad (\text{since }\sin{2φ} = 2\sin{φ} \cos{φ}) \\[4pt] \nonumber &= \int_0^{2\pi} \left ( -\dfrac{a^4}{16} \cos{2φ} \Big |_{φ=0}^{ φ=\pi/2}\right ) \,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \dfrac{a^4}{8}\,dθ \\[4pt] &=\dfrac{\pi a^4}{4}, \\[4pt] \end{align}\]
so
\[\nonumber \bar z = \dfrac{M_{xy}}{M} = \dfrac{\dfrac{\pi a^4}{4}}{\dfrac{2\pi a^3}{3}}=\dfrac{3a}{8}.\]
Thus, the center of mass of \(S\) is \((\bar x,\bar y,\bar z) = \left ( 0,0, \dfrac{3a}{8} \right ).\)


