3.7: Application- Probability and Expectation Values
( \newcommand{\kernel}{\mathrm{null}\,}\)
In this section we will briefly discuss some applications of multiple integrals in the field of probability theory. In particular we will see ways in which multiple integrals can be used to calculate probabilities and expected values.
Probability
Suppose that you have a standard six-sided (fair) die, and you let a variable X represent the value rolled. Then the probability of rolling a 3, written as P(X=3), is 1 6 , since there are six sides on the die and each one is equally likely to be rolled, and hence in particular the 3 has a one out of six chance of being rolled. Likewise the probability of rolling at most a 3, written as P(X≤3), is 36=12, since of the six numbers on the die, there are three equally likely numbers (1, 2, and 3) that are less than or equal to 3. Note that:
P(X≤3)=P(X=1)+P(X=2)+P(X=3).
We call X a discrete random variable on the sample space (or probability space) Ω consisting of all possible outcomes. In our case, Ω=1,2,3,4,5,6. An event A is a subset of the sample space. For example, in the case of the die, the event X≤3 is the set 1,2,3.
Now let X be a variable representing a random real number in the interval (0,1). Note that the set of all real numbers between 0 and 1 is not a discrete (or countable) set of values, i.e. it can not be put into a one-to-one correspondence with the set of positive integers. In this case, for any real number x in (0,1), it makes no sense to consider P(X=x) since it must be 0 (why?). Instead, we consider the probability P(X≤x), which is given by P(X≤x)=x. The reasoning is this: the interval (0,1) has length 1, and for x in (0,1) the interval (0,x) has length x. So since X represents a random number in (0,1), and hence is uniformly distributed over (0,1), then
P(X≤x)=length of (0,x)length of (0,1)=x1=x
We call X a continuous random variable on the sample space Ω=(0,1). An event A is a subset of the sample space. For example, in our case the event X≤x is the set (0,x).
In the case of a discrete random variable, we saw how the probability of an event was the sum of the probabilities of the individual outcomes comprising that event (e.g. P(X≤3)=P(X=1)+P(X=2)+P(X=3) in the die example). For a continuous random variable, the probability of an event will instead be the integral of a function, which we will now describe.
Let X be a continuous real-valued random variable on a sample space Ω in R. For simplicity, let Ω=(a,b). Define the distribution function F of X as
F(x)=P(X≤x),for −∞<x<∞={1,for x≥bP(X≤x),for a<x<b0,for x≤a.
Suppose that there is a nonnegative, continuous real-valued function f on R such that
F(x)=∫x−∞f(y)dy,for −∞<x<∞,
and
∫∞−∞f(x)dx=1
Then we call f the probability density function (or p.d.f. for short) for X. We thus have
P(X≤x)=∫xaf(y)dy,for a<x<b
Also, by the Fundamental Theorem of Calculus, we have
F′(x)=f(x),for −∞<x<∞.
Example 3.7.1: Uniform Distribution
Let X represent a randomly selected real number in the interval (0,1). We say that X has the uniform distribution on (0,1), with distribution function
F(x)=P(X≤x)={1,for x≥1x,for 0<x<10,for x≤0,
and probability density function
f(x)=F′(x)={1,for 0<x<10,elsewhere.
In general, if X represents a randomly selected real number in an interval (a,b), then X has the uniform distribution function
F(x)=P(X≤x)={1,\text{for }x \ge b xb−a,\text{for }a<x<b 0,\text{for }x \le a
f(x)=F′(x)={1b−a,\text{for }a<x<b 0,elsewhere.
Example 3.7.2: Standard Normal Distribution
A famous distribution function is given by the standard normal distribution, whose probability density function f is
f(x)=1√2πe−x2/2,for −∞<x<∞
This is often called a “bell curve”, and is used widely in statistics. Since we are claiming that f is a p.d.f., we should have
∫∞−∞1√2πe−x2/2dx=1
by Equation ???, which is equivalent to
∫∞−∞e−x2/2dx=√2π.
We can use a double integral in polar coordinates to verify this integral. First,
∫∞−∞∫∞−∞e−(x2+y2)/2dxdy=∫∞−∞e−y2/2(∫∞−∞e−x2/2dx)dy=(∫∞−∞e−x2/2dx)(∫∞−∞e−y2/2dy)=(∫∞−∞e−x2/2dx)2
since the same function is being integrated twice in the middle equation, just with different variables. But using polar coordinates, we see that
\nonumber \begin{align} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} e^{-(x^2+y^2)/2} \, dx\,dy &=\int_0^{2\pi} \int_0^\infty e^{-r^2/2}\,r\,dr\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} \left (-e^{-r^2/2} \Big |_{r=0}^{r=\infty} \right )\,dθ \\[4pt] \nonumber &=\int_0^{2\pi} (0-(-e^0))\,dθ = \int_0^{2\pi}1\,dθ=2\pi , \\[4pt] \end{align}
and so
\nonumber \begin{align}\left ( \int_{-\infty}^{\infty} e^{-x^2/2}\,dx \right )^2 &= 2\pi,\text{ and hence }\\[4pt] \nonumber \int_{-\infty}^{\infty} e^{-x^2/2}\,dx &= \sqrt{2\pi} \\[4pt] \end{align}
In addition to individual random variables, we can consider jointly distributed random variables. For this, we will let X, Y \text{ and }Z be three real-valued continuous random variables defined on the same sample space Ω in \mathbb{R} (the discussion for two random variables is similar). Then the joint distribution function F \text{ of }X, Y \text{ and }Z is given by
F(x, y, z) = P(X ≤ x, Y ≤ y, Z ≤ z) ,\text{ for }-\infty < x,y,z < \infty. \label{Eq3.46}
If there is a nonnegative, continuous real-valued function f on \mathbb{R}^ 3 such that
F(x,y,z) = \int_{-\infty}^z \int_{-\infty}^y \int_{-\infty}^x f (u,v,w)\,du\, dv\, dw, \text{ for }-\infty <x,y,z< \infty \label{Eq3.47}
and
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f (x, y, z)\,dx\, d y\, dz = 1 ,\label{Eq3.48}
then we call f the joint probability density function (or joint p.d.f. for short) for X, Y \text{ and }Z. In general, for a_1 < b_1 , a_2 < b_2 , a_3 < b_3, we have
P(a_1 < X ≤ b_1 , a_2 < Y ≤ b_2 , a_3 < Z ≤ b_3) = \int_{a_3}^{b_3} \int_{a_2}^{b_2} \int_{a_1}^{b_1}f (x, y, z)\,dx\, d y\, dz ,\label{Eq3.49}
with the \le \text{ and }< symbols interchangeable in any combination. A triple integral, then, can be thought of as representing a probability (for a function f which is a p.d.f.).
Example \PageIndex{3}
Let a, b, \text{ and }c be real numbers selected randomly from the interval (0,1). What is the probability that the equation ax^2 + bx+ c = 0 has at least one real solution x?
Solution
We know by the quadratic formula that there is at least one real solution if b^2−4ac ≥ 0. So we need to calculate P(b^2−4ac ≥ 0). We will use three jointly distributed random variables to do this. First, since 0 < a,b, c < 1, we have
\nonumber b^2 −4ac ≥ 0 ⇔ 0 < 4ac ≤ b^2 < 1 ⇔ 0 < 2 \sqrt{ a} \sqrt{ c} ≤ b < 1 ,
where the last relation holds for all 0 < a, c < 1 such that
\nonumber 0 < 4ac < 1 ⇔ 0 < c < \dfrac{1}{4a}
Considering a, b \text{ and }c as real variables, the region R in the ac-plane where the above relation holds is given by R = {(a, c) : 0 < a < 1, 0 < c < 1, 0 < c < \dfrac{1}{4a} }, which we can see is a union of two regions R_1 and R_2, as in Figure \PageIndex{1}.
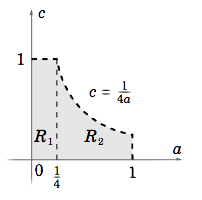
Now let X, Y \text{ and }Z be continuous random variables, each representing a randomly selected real number from the interval (0,1) (think of X, Y \text{ and }Z representing a, b \text{ and }c, respectively). Then, similar to how we showed that f (x) = 1 is the p.d.f. of the uniform distribution on (0,1), it can be shown that f (x, y, z) = 1 \text{ for }x, y, z in (0,1) (0 elsewhere) is the joint p.d.f. \text{ of }X, Y \text{ and }Z. Now,
\nonumber P(b^2 −4ac ≥ 0) = P((a, c) ∈ R, 2 \sqrt{ a} \sqrt{ c} ≤ b < 1) ,
so this probability is the triple integral of f (a,b, c) = 1 as b varies from 2\sqrt{ a}\sqrt{c} to 1 and as (a, c) varies over the region R. Since R can be divided into two regions R_1 \text{ and }R_2, then the required triple integral can be split into a sum of two triple integrals, using vertical slices in R:
\nonumber \begin{align} P(b^2 −4ac ≥ 0) &= \underbrace{\int_0^{1/4} \int_0^1}_{R_1}\int_{2\sqrt{a}\sqrt{c}}^1 1\,db\, dc\, da + \underbrace{\int_{1/4}^1 \int_0^{1/4a}}_{R_2} \int_{2\sqrt{a}\sqrt{c}}^1 1\,db\, dc\, da \\[4pt] \nonumber &= \int_0^{1/4} \int_0^1 (1−2 \sqrt{ a} \sqrt{ c})dc \,da + \int_{1/4}^1 \int_0^{1/4a}(1−2 \sqrt{ a} \sqrt{ c})dc\, da \\[4pt] \nonumber &= \int_0^{1/4} \left ( c-\dfrac{4}{3}\sqrt{a}c^{3/2}\Big |_{c=0}^{c=1} \right )\,da+\int_{1/4}^1 \left (c-\dfrac{4}{3}\sqrt{a}c^{3/2}\Big |_{c=0}^{c=1/4a} \right )\,da \\[4pt] \nonumber &=\int_0^{1/4} \left (1-\dfrac{4}{3}\sqrt{a} \right )\,da+\int_{1/4}^1 \dfrac{1}{12a}\,da \\[4pt] \nonumber &=a-\dfrac{8}{9}a^{3/2} \Big |_0^{1/4}+\dfrac{1}{12}\ln a \Big |_{1/4}^1 \\[4pt] \nonumber &=\left (\dfrac{1}{4}-\dfrac{1}{9} \right ) + \left (0-\dfrac{1}{12}\ln \dfrac{1}{4} \right ) = \dfrac{5}{36} + \dfrac{1}{12}\ln 4 \\[4pt] \nonumber P(b^2 −4ac ≥ 0) &= \dfrac{5+3\ln 4}{36} \approx 0.2544 \\[4pt] \end{align}
In other words, the equation ax^2 + bx+ c = 0 has about a 25% chance of being solved!
Expectation Value
The expectation value (or expected value) EX of a random variable X can be thought of as the “average” value of X as it varies over its sample space. If X is a discrete random variable, then
EX = \sum_x xP(X = x) ,\label{Eq3.50}
with the sum being taken over all elements x of the sample space. For example, if X represents the number rolled on a six-sided die, then
EX = \sum_{x=1}^6 x P(X = x) = \sum_{x=1}^6 x\dfrac{1}{6} = 3.5 \label{Eq3.51}
is the expected value of X, which is the average of the integers 1−6.
If X is a real-valued continuous random variable with p.d.f. f, then
EX = \int_{-\infty}^\infty x f (x)\,dx \label{Eq3.52}
For example, if X has the uniform distribution on the interval (0,1), then its p.d.f. is
f(x) = \cases{1, \quad &\text{for }0 < x < 1 \\[4pt] 0,&\text{elsewhere}}\label{Eq3.53}
and so
EX=\int_{-\infty}^\infty x f (x)\,dx = \int_0^1 x\,dx = \dfrac{1}{2} \label{Eq3.54}
For a pair of jointly distributed, real-valued continuous random variables X and Y with joint p.d.f. f (x, y), the expected values of X \text{ and }Y are given by
EX = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} xf(x,y)\,dx\,dy \text{ and } EY = \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} yf(x,y)\,dx\,dy \label{Eq3.55}
respectively.
Example \PageIndex{4}
If you were to pick n > 2 random real numbers from the interval (0,1), what are the expected values for the smallest and largest of those numbers?
Solution
Let U_1 ,...,U_n be n continuous random variables, each representing a randomly selected real number from (0,1), i.e. each has the uniform distribution on (0,1). Define random variables X \text{ and }Y by
\nonumber X=\text{min}(U_1,...,U_n)\text{ and }Y=\text{max}(U_1,...,U_n).
Then it can be shown that the joint p.d.f. of X \text{ and }Y is
f(x,y) = \cases{n(n−1)(y− x)^{n−2},\quad &\text{for } 0 ≤ x ≤ y ≤ 1 \\[4pt] 0, &\text{elsewhere.}}\label{Eq3.56}
Thus, the expected value of X is
\nonumber \begin{align} EX &=\int_0^1 \int_x^1 n(n−1)x(y− x)^{n−2}\, d y\, dx \\[4pt] \nonumber &=\int_0^1 \left ( nx(y− x)^{n−1} \Big |_{y=x}^{y=1} \right )\,dx \\[4pt] \nonumber &=\int_0^1 nx(1− x)^{n−1}\, dx,\text{ so integration by parts yields} \\[4pt] \nonumber &=−x(1− x)^n − \dfrac{1}{n+1} (1− x)^{n+1} \Big |_0^1 \\[4pt] \nonumber EX&=\dfrac{1}{n+1}, \\[4pt] \end{align}
and similarly (see Exercise 3) it can be shown that
\nonumber EY = \int_0^1 \int_0^y n(n−1)y(y− x)^{n−2}\, dx\, d y = \dfrac{n}{n+1}.
So, for example, if you were to repeatedly take samples of n = 3 random real numbers from (0,1), and each time store the minimum and maximum values in the sample, then the average of the minimums would approach \dfrac{1}{ 4} and the average of the maximums would approach \dfrac{3}{ 4} as the number of samples grows. It would be relatively simple (see Exercise 4) to write a computer program to test this.



