1.6: The Derivatives

We now return to the problem of rates of change. Given \(y=f(x),\) for any infinitesimal \(d x\) we let

\[d y=f(x+d x)-f(x) .\] If \(y\) is a continuous function of \(x,\) then \(d y\) is infinitesimal and, if \(d x \neq 0,\) the ratio \[\frac{d y}{d x}=\frac{f(x+d x)-f(x)}{d x}\] is a hyperreal number. If \(\frac{d y}{d x}\) is finite, then its shadow, if it is the same for all values of \(d x,\) is the rate of change of \(y\) with respect to \(x,\) which we will call the derivative of \(y\) with respect to \(x .\)

Definition

Given \(y=f(x),\) suppose

\[\frac{d y}{d x}=\frac{f(x+d x)-f(x)}{d x}\] is finite and has the same shadow for all nonzero infinitesimals \(d x .\) Then we call \[\operatorname{sh}\left(\frac{d y}{d x}\right)\] the derivative of \(y\) with respect to \(x .\)

Note that the quotient in \((1.6 .3)\) will be infinite if \(f(x+d x)-f(x)\) is not an infinitesimal. Hence a function which is not continuous at \(x\) cannot have a derivative at \(x .\)

There are numerous ways to denote the derivative of a function \(y=f(x) .\) One is to use \(\frac{d y}{d x}\) to denote, depending on the context, both the ratio of the infinitesimals \(d y\) and \(d x\) and the shadow of this ratio, which is the derivative. Another is to write \(f^{\prime}(x)\) for the derivative of the function \(f .\) We will use both of these notations extensively.

Example \(\PageIndex{1}\)

If \(y=x^{2},\) then, for any nonzero infinitesimal \(d x\),

\[d y=(x+d x)^{2}-x^{2}=\left(x^{2}+2 x d x+(d x)^{2}\right)-x^{2}=(2 x+d x) d x .\] Hence \[\frac{d y}{d x}=2 x+d x \simeq 2 x\] and so the derivative of \(y\) with respect to \(x\) is \[\frac{d y}{d x}=2 x.\]

Example \(\PageIndex{2}\)

If \(f(x)=4 x,\) then, for any nonzero infinitesimal \(d x\),

\[\frac{f(x+d x)-f(x)}{d x}=\frac{4(x+d x)-4 x}{d x}=\frac{4 d x}{d x}=4 .\] Hence \(f^{\prime}(x)=4 .\) Note that this implies that \(f(x)\) has a constant rate of change: every change of one unit in \(x\) results in a change of 4 units in \(f(x) .\)

Exercise \(\PageIndex{1}\)

Find \(\frac{d y}{d x}\) if \(y=5 x-2\).

Answer

\(\frac{d y}{d x}=5\)

Exercise \(\PageIndex{2}\)

Find \(\frac{d y}{d x}\) if \(y=x^{3}\).

Answer

\(\frac{d y}{d x}=3 x^{2}\)

Exercise \(\PageIndex{3}\)

Find \(f^{\prime}(x)\) if \(f(x)=4 x^{2}\).

To denote the rate of change of \(y\) with respect to \(x\) at a particular value of \(x,\) say, when \(x=a,\) we write \[\left.\frac{d y}{d x}\right|_{x=a}.\] If \(y=f(x),\) then, of course, this is the same as writing \(f^{\prime}(a)\).

Answer

\(f^{\prime}(x)=8 x\)

Example \(\PageIndex{3}\)

If \(y=x^{2},\) then we saw above that \(\frac{d y}{d x}=2 x .\) Hence the rate of change of \(y\) with respect to \(x\) when \(x=3\) is

\[\left.\frac{d y}{d x}\right|_{x=3}=(2)(3)=6 .\]

Example \(\PageIndex{4}\)

If \(f(x)=x^{\frac{2}{3}},\) then for any infinitesimal \(d x\),

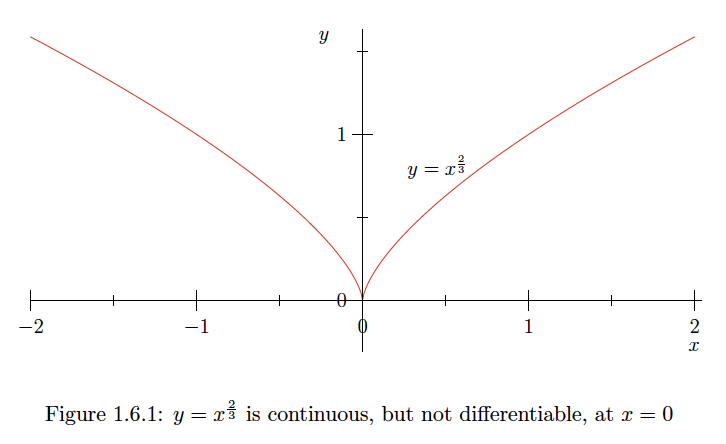
\[f(0+d x)-f(0)=f(d x)=(d x)^{\frac{2}{3}} ,\] which is infinitesimal. Hence \(f\) is continuous at \(x=0 .\) Now if \(d x \neq 0,\) then \[\frac{f(0+d x)-f(0)}{d x}=\frac{(d x)^{\frac{2}{3}}}{d x}=\frac{1}{(d x)^{\frac{1}{3}}} .\] Since this is infinite, \(f\) does not have a derivative at \(x=0 .\) In particular, this shows that a function may be continuous at a point, but not differentiable at that point. See Figure \(1.6 .1 .\)

Example \(\PageIndex{5}\)

If \(f(x)=\sqrt{x},\) then, as we have seen above, for any \(x>0\) and any nonzero infinitesimal \(d x\),

\[\begin{aligned} f(x+d x)-f(x) &=\sqrt{x+d x}-\sqrt{x} \\[8pt] &=(\sqrt{x+d x}-\sqrt{x}) \frac{\sqrt{x+d x}+\sqrt{x}}{\sqrt{x+d x}+\sqrt{x}} \\[8pt] &=\frac{(x+d x)-x}{\sqrt{x+d x}+\sqrt{x}} \\[8pt] &=\frac{d x}{\sqrt{x+d x}+\sqrt{x}}. \end{aligned}\] It now follows that \[\frac{f(x+d x)-f(x)}{d x}=\frac{1}{\sqrt{x+d x}+\sqrt{x}} \simeq \frac{1}{\sqrt{x}+\sqrt{x}}=\frac{1}{2 \sqrt{x}} .\] Thus \[f^{\prime}(x)=\frac{1}{2 \sqrt{x}} .\] For example, the rate of change of \(y\) with respect to \(x\) when \(x=9\) is \[f^{\prime}(9)=\frac{1}{2 \sqrt{9}}=\frac{1}{6} .\] We will sometimes also write \[\frac{d}{d x} f(x)\] for \(f^{\prime}(x) .\) With this notation, we could write the result of the previous example as \[\frac{d}{d x} \sqrt{x}=\frac{1}{2 \sqrt{x}} .\]

Definition

Given a function \(f,\) if \(f^{\prime}(a)\) exists we say \(f\) is differentiable at \(a .\) We say \(f\) is differentiable on an open interval \((a, b)\) if \(f\) is differentiable at each point \(x\) in \((a, b) .\)

Example \(\PageIndex{6}\)

The function \(y=x^{2}\) is differentiable on \((-\infty, \infty)\).

Example \(\PageIndex{7}\)

The function \(f(x)=\sqrt{x}\) is differentiable on \((0, \infty) .\) Note that \(f\) is not differentiable at \(x=0\) since \(f(0+d x)=f(d x)\) is not defined for all infinitesimals \(d x .\)

Example \(\PageIndex{8}\)

The function \(f(x)=x^{\frac{2}{3}}\) is not differentiable at \(x=0\).