1.8: A Geometric Interpretation of the Derivatives

Last updated
Save as PDF

Page ID: 25429

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recall that if $y=f(x),$ then, for any real number $\Delta x$,

\[\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}\] is the average rate of change of $y$ with respect to $x$ over the interval $[x, x+\Delta x]$ (see $(1.2 .7)) .$ Now if the graph of $y$ is a straight line, that is, if $f(x)=m x+b$ for some real numbers $m$ and $b,$ then $(1.8 .1)$ is $m,$ the slope of the line. In fact, a straight line is characterized by the fact $(1.8 .1)$ is the same for any values of $x$ and $\Delta x .$ Moreover, $(1.8 .1)$ remains the same when $\Delta x$ is infinitesimal; that is, the derivative of $y$ with respect to $x$ is the slope of the line. For other differentiable functions $f,$ the value of $(1.8 .1)$ depends upon both $x$ and $\Delta x .$ However, for infinitesimal values of $\Delta x,$ the shadow of $(1.8 .1),$ that is, the derivative $\frac{d y}{d x},$ depends on $x$ alone. Hence it is reasonable to think of $\frac{d y}{d x}$ as the slope of the curve $y=f(x)$ at a point $x .$ Whereas the slope of a straight line is constant from point to point, for other differentiable functions the value of the slope of the curve will vary from point to point. If $f$ is differentiable at a point $a,$ we call the line with slope $f^{\prime}(a)$ passing through $(a, f(a))$ the tangent line to the graph of $f$ at $(a, f(a)) .$ That is, the tangent line to the graph of $y=f(x)$ at $x=a$ is the line with equation \[y=f^{\prime}(a)(x-a)+f(a) .\] Hence a tangent line to the graph of a function $f$ is a line through a point on the graph of $f$ whose slope is equal to the slope of the graph at that point.

Example $\PageIndex{1}$

If $f(x)=x^{5}-6 x^{2}+5,$ then

\[f^{\prime}(x)=5 x^{4}-12 x .\] In particular, $f^{\prime}\left(-\frac{1}{2}\right)=\frac{101}{16},$ and so the equation of the line tangent to the graph of $f$ at $x=-\frac{1}{2}$ is \[y=\frac{101}{6}\left(x+\frac{1}{2}\right)+\frac{111}{32} .\] See Figure 1.8.1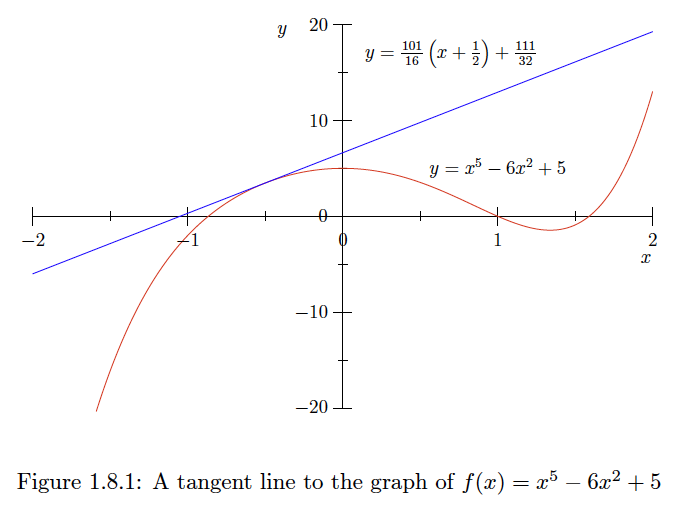

$Screen Shot 2019-11-15 at 10.50.21 PM.png$

Exercise $\PageIndex{1}$

Find an equation for the line tangent to the graph of

\[f(x)=3 x^{4}-6 x+3\] at $x=2$.

Answer: $y=90(x-2)+39$

Exercise $\PageIndex{2}$

Find an equation for the line tangent to the graph of

\[y=3 \sin ^{2}(x)\] at $x=\frac{\pi}{4}$.

Answer: $y=3\left(t-\frac{\pi}{4}\right)+\frac{3}{2}$