12.6: Quadric Surfaces

Learning Objectives

• Identify a cylinder as a type of three-dimensional surface.
• Recognize the main features of ellipsoids, paraboloids, and hyperboloids.
• Use traces to draw the intersections of quadric surfaces with the coordinate planes.

We have been exploring vectors and vector operations in three-dimensional space, and we have developed equations to describe lines, planes, and spheres. In this section, we use our knowledge of planes and spheres, which are examples of three-dimensional figures called surfaces, to explore a variety of other surfaces that can be graphed in a three-dimensional coordinate system.

Identifying Cylinders

The first surface we’ll examine is the cylinder. Although most people immediately think of a hollow pipe or a soda straw when they hear the word cylinder, here we use the broad mathematical meaning of the term. As we have seen, cylindrical surfaces don’t have to be circular. A rectangular heating duct is a cylinder, as is a rolled-up yoga mat, the cross-section of which is a spiral shape.

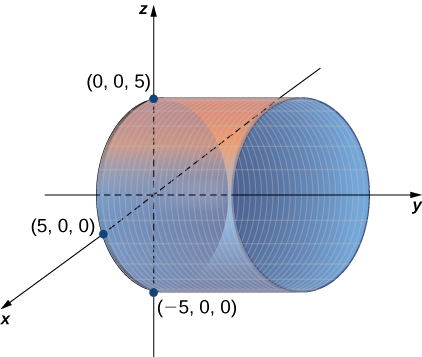
In the two-dimensional coordinate plane, the equation describes a circle centered at the origin with radius . In three-dimensional space, this same equation represents a surface. Imagine copies of a circle stacked on top of each other centered on the -axis (Figure ), forming a hollow tube. We can then construct a cylinder from the set of lines parallel to the -axis passing through the circle in the -plane, as shown in the figure. In this way, any curve in one of the coordinate planes can be extended to become a surface.

Figure : In three-dimensional space, the graph of equation is a cylinder with radius centered on the -axis. It continues indefinitely in the positive and negative directions.

Definition: cylinders and rulings

A set of lines parallel to a given line passing through a given curve is known as a cylindrical surface, or cylinder. The parallel lines are called rulings.

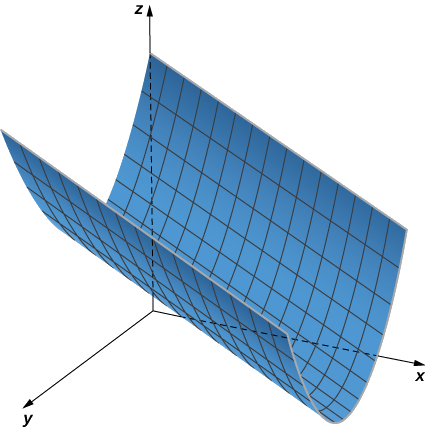
From this definition, we can see that we still have a cylinder in three-dimensional space, even if the curve is not a circle. Any curve can form a cylinder, and the rulings that compose the cylinder may be parallel to any given line (Figure ).

Figure : In three-dimensional space, the graph of equation is a cylinder, or a cylindrical surface with rulings parallel to the -axis.

Example : Graphing Cylindrical Surfaces

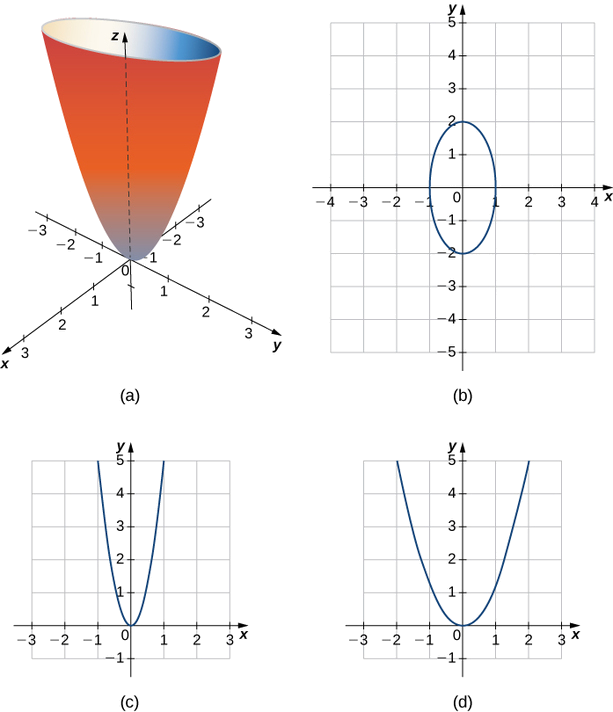
Sketch the graphs of the following cylindrical surfaces.

Solution

a. The variable can take on any value without limit. Therefore, the lines ruling this surface are parallel to the -axis. The intersection of this surface with the -plane forms a circle centered at the origin with radius (see Figure ).

Figure : The graph of equation is a cylinder with radius centered on the -axis.

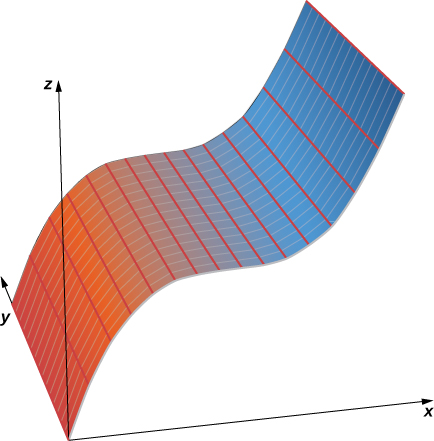
b. In this case, the equation contains all three variables — and — so none of the variables can vary arbitrarily. The easiest way to visualize this surface is to use a computer graphing utility (Figure ).

Figure

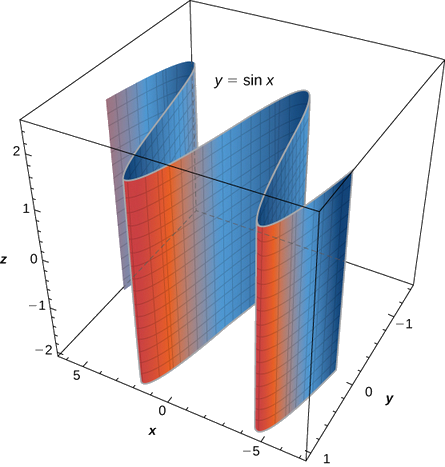
c. In this equation, the variable can take on any value without limit. Therefore, the lines composing this surface are parallel to the -axis. The intersection of this surface with the -plane outlines curve (Figure ).

Figure : The graph of equation is formed by a set of lines parallel to the -axis passing through curve in the -plane.

Exercise :

Sketch or use a graphing tool to view the graph of the cylindrical surface defined by equation .

Hint

The variable can take on any value without limit.

Answer

When sketching surfaces, we have seen that it is useful to sketch the intersection of the surface with a plane parallel to one of the coordinate planes. These curves are called traces. We can see them in the plot of the cylinder in Figure .

Definition: traces

The traces of a surface are the cross-sections created when the surface intersects a plane parallel to one of the coordinate planes.

Traces are useful in sketching cylindrical surfaces. For a cylinder in three dimensions, though, only one set of traces is useful. Notice, in Figure , that the trace of the graph of in the -plane is useful in constructing the graph. The trace in the -plane, though, is just a series of parallel lines, and the trace in the -plane is simply one line.

Figure : (a) This is one view of the graph of equation . (b) To find the trace of the graph in the -plane, set . The trace is simply a two-dimensional sine wave.

Cylindrical surfaces are formed by a set of parallel lines. Not all surfaces in three dimensions are constructed so simply, however. We now explore more complex surfaces, and traces are an important tool in this investigation.

Quadric Surfaces

We have learned about surfaces in three dimensions described by first-order equations; these are planes. Some other common types of surfaces can be described by second-order equations. We can view these surfaces as three-dimensional extensions of the conic sections we discussed earlier: the ellipse, the parabola, and the hyperbola. We call these graphs quadric surfaces

Definition: Quadric surfaces and conic sections

Quadric surfaces are the graphs of equations that can be expressed in the form

When a quadric surface intersects a coordinate plane, the trace is a conic section.

An ellipsoid is a surface described by an equation of the form Set to see the trace of the ellipsoid in the -plane. To see the traces in the - and -planes, set and , respectively. Notice that, if , the trace in the -plane is a circle. Similarly, if , the trace in the -plane is a circle and, if , then the trace in the -plane is a circle. A sphere, then, is an ellipsoid with

Example : Sketching an Ellipsoid

Sketch the ellipsoid

Solution

Start by sketching the traces. To find the trace in the -plane, set (Figure ). To find the other traces, first set and then set

Figure : (a) This graph represents the trace of equation in the -plane, when we set . (b) When we set , we get the trace of the ellipsoid in the -plane, which is an ellipse. (c) When we set , we get the trace of the ellipsoid in the -plane, which is also an ellipse.

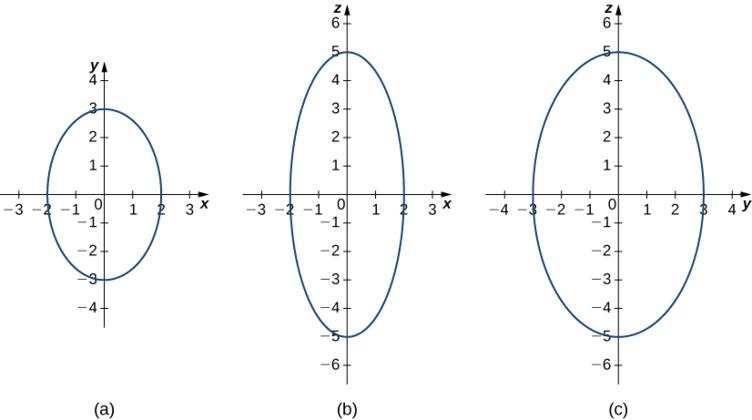
Now that we know what traces of this solid look like, we can sketch the surface in three dimensions (Figure ).

Figure : (a) The traces provide a framework for the surface. (b) The center of this ellipsoid is the origin.

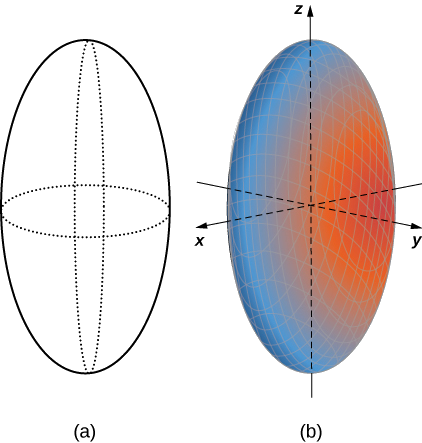
The trace of an ellipsoid is an ellipse in each of the coordinate planes. However, this does not have to be the case for all quadric surfaces. Many quadric surfaces have traces that are different kinds of conic sections, and this is usually indicated by the name of the surface. For example, if a surface can be described by an equation of the form

then we call that surface an elliptic paraboloid. The trace in the xy-plane is an ellipse, but the traces in the -plane and -plane are parabolas (Figure ). Other elliptic paraboloids can have other orientations simply by interchanging the variables to give us a different variable in the linear term of the equation or .

Figure : This quadric surface is called an elliptic paraboloid.

Example : Identifying Traces of Quadric Surfaces

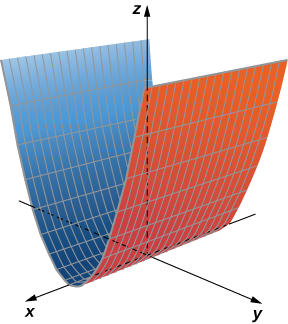
Describe the traces of the elliptic paraboloid .

Solution

To find the trace in the -plane, set The trace in the plane is simply one point, the origin. Since a single point does not tell us what the shape is, we can move up the -axis to an arbitrary plane to find the shape of other traces of the figure.

The trace in plane is the graph of equation , which is an ellipse. In the -plane, the equation becomes . The trace is a parabola in this plane and in any plane with the equation .

In planes parallel to the -plane, the traces are also parabolas, as we can see in Figure .

Figure : (a) The paraboloid . (b) The trace in plane . (c) The trace in the -plane. (d) The trace in the -plane.

Exercise :

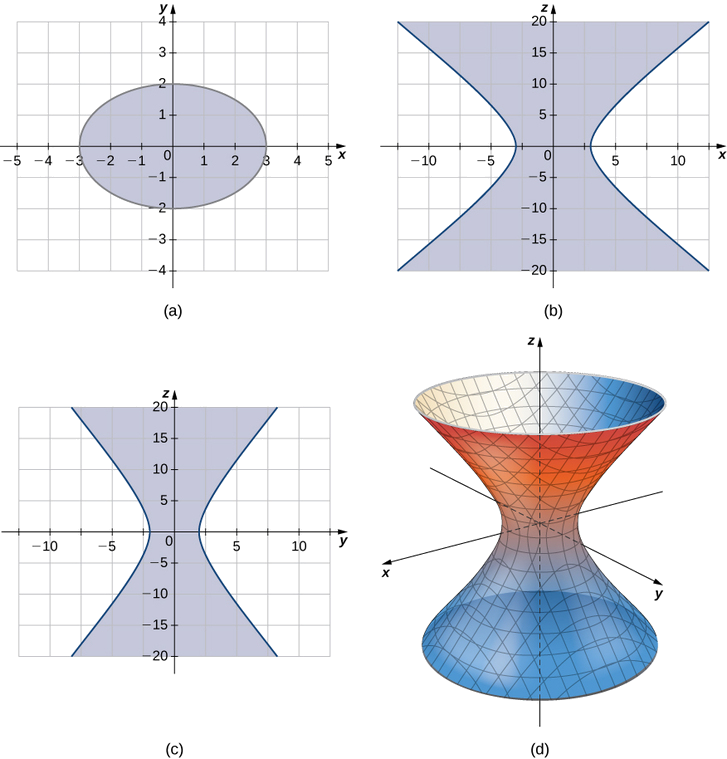
A hyperboloid of one sheet is any surface that can be described with an equation of the form . Describe the traces of the hyperboloid of one sheet given by equation

Hint

To find the traces in the coordinate planes, set each variable to zero individually.

Answer

The traces parallel to the -plane are ellipses and the traces parallel to the - and -planes are hyperbolas. Specifically, the trace in the -plane is ellipse the trace in the -plane is hyperbola and the trace in the -plane is hyperbola (see the following figure).

Hyperboloids of one sheet have some fascinating properties. For example, they can be constructed using straight lines, such as in the sculpture in Figure . In fact, cooling towers for nuclear power plants are often constructed in the shape of a hyperboloid. The builders are able to use straight steel beams in the construction, which makes the towers very strong while using relatively little material (Figure ).

Figure : (a) A sculpture in the shape of a hyperboloid can be constructed of straight lines. (b) Cooling towers for nuclear power plants are often built in the shape of a hyperboloid.

Example : Chapter Opener: Finding the Focus of a Parabolic Reflector

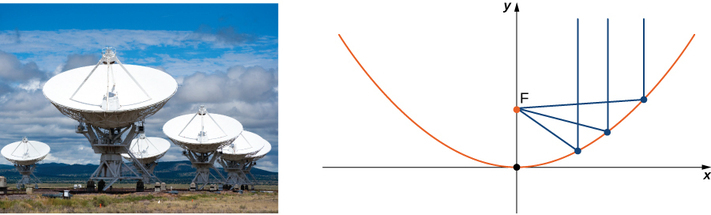
Energy hitting the surface of a parabolic reflector is concentrated at the focal point of the reflector (Figure ). If the surface of a parabolic reflector is described by equation where is the focal point of the reflector?

Figure : Energy reflects off of the parabolic reflector and is collected at the focal point. (credit: modification of CGP Grey, Wikimedia Commons)

Solution

Since is the first-power variable, the axis of the reflector corresponds to the -axis. The coefficients of and are equal, so the cross-section of the paraboloid perpendicular to the -axis is a circle. We can consider a trace in the -plane or the -plane; the result is the same. Setting , the trace is a parabola opening up along the -axis, with standard equation , where is the focal length of the parabola. In this case, this equation becomes or . So is m, which tells us that the focus of the paraboloid is m up the axis from the vertex. Because the vertex of this surface is the origin, the focal point is

Seventeen standard quadric surfaces can be derived from the general equation

The following figures summarize the most important ones.

Figure : Characteristics of Common Quadric Surfaces: Ellipsoid, Hyperboloid of One Sheet, Hyperboloid of Two Sheets.

Figure : Characteristics of Common Quadric Surfaces: Elliptic Cone, Elliptic Paraboloid, Hyperbolic Paraboloid.

Example : Identifying Equations of Quadric Surfaces

Identify the surfaces represented by the given equations.

Solution

a. The and terms are all squared, and are all positive, so this is probably an ellipsoid. However, let’s put the equation into the standard form for an ellipsoid just to be sure. We have

Dividing through by 144 gives

So, this is, in fact, an ellipsoid, centered at the origin.

b. We first notice that the term is raised only to the first power, so this is either an elliptic paraboloid or a hyperbolic paraboloid. We also note there are terms and terms that are not squared, so this quadric surface is not centered at the origin. We need to complete the square to put this equation in one of the standard forms. We have

This is an elliptic paraboloid centered at

Exercise

Identify the surface represented by equation

Hint

Look at the signs and powers of the , and terms

Answer

Hyperboloid of one sheet, centered at .

Key Concepts

• A set of lines parallel to a given line passing through a given curve is called a cylinder, or a cylindrical surface. The parallel lines are called rulings.
• The intersection of a three-dimensional surface and a plane is called a trace. To find the trace in the -, -, or -planes, set or respectively.
• Quadric surfaces are three-dimensional surfaces with traces composed of conic sections. Every quadric surface can be expressed with an equation of the form

• To sketch the graph of a quadric surface, start by sketching the traces to understand the framework of the surface.
• Important quadric surfaces are summarized in Figures and .

Glossary

cylinder

a set of lines parallel to a given line passing through a given curve

ellipsoid

a three-dimensional surface described by an equation of the form ; all traces of this surface are ellipses

elliptic cone

a three-dimensional surface described by an equation of the form ; traces of this surface include ellipses and intersecting lines

elliptic paraboloid

a three-dimensional surface described by an equation of the form ; traces of this surface include ellipses and parabolas

hyperboloid of one sheet

a three-dimensional surface described by an equation of the form traces of this surface include ellipses and hyperbolas

hyperboloid of two sheets

a three-dimensional surface described by an equation of the form ; traces of this surface include ellipses and hyperbolas

quadric surfaces

surfaces in three dimensions having the property that the traces of the surface are conic sections (ellipses, hyperbolas, and parabolas)

rulings

parallel lines that make up a cylindrical surface

trace

the intersection of a three-dimensional surface with a coordinate plane