Search

Text Color

Margin Size

Font Type

Enable Dyslexic Font

9.1: Area Between Curves

Last updated

Feb 8, 2025
Save as PDF
- 9: Applications of Integration
- 9.2: Distance, Velocity, and Acceleration

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$ $\newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$ $\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$ $\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$ $\newcommand{\AA}{\unicode[.8,0]{x212B}}$

$\newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$\newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$\newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vectorC}[1]{\textbf{#1}}$

$\newcommand{\vectorD}[1]{\overrightarrow{#1}}$

$\newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}}$

$\newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}}$

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\avec}{\mathbf a}$

$\newcommand{\bvec}{\mathbf b}$

$\newcommand{\cvec}{\mathbf c}$

$\newcommand{\dvec}{\mathbf d}$

$\newcommand{\dtil}{\widetilde{\mathbf d}}$

$\newcommand{\evec}{\mathbf e}$

$\newcommand{\fvec}{\mathbf f}$

$\newcommand{\nvec}{\mathbf n}$

$\newcommand{\pvec}{\mathbf p}$

$\newcommand{\qvec}{\mathbf q}$

$\newcommand{\svec}{\mathbf s}$

$\newcommand{\tvec}{\mathbf t}$

$\newcommand{\uvec}{\mathbf u}$

$\newcommand{\vvec}{\mathbf v}$

$\newcommand{\wvec}{\mathbf w}$

$\newcommand{\xvec}{\mathbf x}$

$\newcommand{\yvec}{\mathbf y}$

$\newcommand{\zvec}{\mathbf z}$

$\newcommand{\rvec}{\mathbf r}$

$\newcommand{\mvec}{\mathbf m}$

$\newcommand{\zerovec}{\mathbf 0}$

$\newcommand{\onevec}{\mathbf 1}$

$\newcommand{\real}{\mathbb R}$

$\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$

$\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$

$\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$

$\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$

$\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$

$\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$

$\newcommand{\laspan}[1]{\text{Span}\{#1\}}$

$\newcommand{\bcal}{\cal B}$

$\newcommand{\ccal}{\cal C}$

$\newcommand{\scal}{\cal S}$

$\newcommand{\wcal}{\cal W}$

$\newcommand{\ecal}{\cal E}$

$\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$

$\newcommand{\gray}[1]{\color{gray}{#1}}$

$\newcommand{\lgray}[1]{\color{lightgray}{#1}}$

$\newcommand{\rank}{\operatorname{rank}}$

$\newcommand{\row}{\text{Row}}$

$\newcommand{\col}{\text{Col}}$

$\renewcommand{\row}{\text{Row}}$

$\newcommand{\nul}{\text{Nul}}$

$\newcommand{\var}{\text{Var}}$

$\newcommand{\corr}{\text{corr}}$

$\newcommand{\len}[1]{\left|#1\right|}$

$\newcommand{\bbar}{\overline{\bvec}}$

$\newcommand{\bhat}{\widehat{\bvec}}$

$\newcommand{\bperp}{\bvec^\perp}$

$\newcommand{\xhat}{\widehat{\xvec}}$

$\newcommand{\vhat}{\widehat{\vvec}}$

$\newcommand{\uhat}{\widehat{\uvec}}$

$\newcommand{\what}{\widehat{\wvec}}$

$\newcommand{\Sighat}{\widehat{\Sigma}}$

$\newcommand{\lt}{<}$

$\newcommand{\gt}{>}$

$\newcommand{\amp}{&}$

$\definecolor{fillinmathshade}{gray}{0.9}$

We have seen how integration can be used to find an area between a curve and the $x$ -axis. With very little change we can find some areas between curves; indeed, the area between a curve and the $x$ -axis may be interpreted as the area between the curve and a second "curve'' with equation $y=0$ . In the simplest of cases, the idea is quite easy to understand.

we show the two curves together, with the desired area shaded, then $f$ alone with the area under $f$ shaded, and then $g$ alone with the area under $g$ shaded.

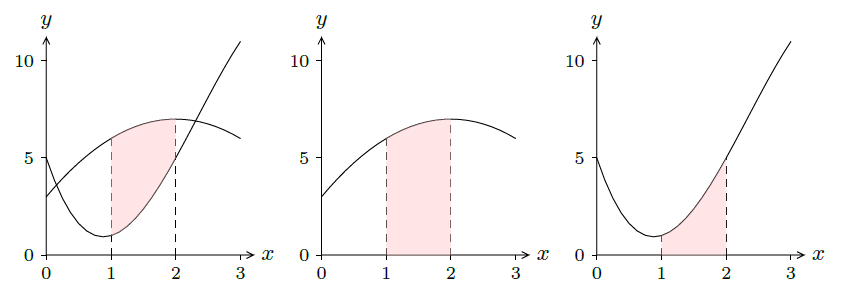
$Area between curves as a difference of areas.$
Figure 9.1.1. Area between curves as a difference of areas.

It is clear from the figure that the area we want is the area under $f$ minus the area under $g$ , which is to say

$\int_1^2 f(x)\,dx-\int_1^2 g(x)\,dx = \int_1^2 f(x)-g(x)\,dx.$ It doesn't matter whether we compute the two integrals on the left and then subtract or compute the single integral on the right. In this case, the latter is perhaps a bit easier:

$\eqalign{ \int_1^2 f(x)-g(x)\,dx&=\int_1^2 -x^2+4x+3-(-x^3+7x^2-10x+5)\,dx\cr &=\int_1^2 x^3-8x^2+14x-2\,dx\cr &=\left.{x^4\over4}-{8x^3\over3}+7x^2-2x\right|_1^2\cr &={16\over4}-{64\over3}+28-4-({1\over4}-{8\over3}+7-2)\cr &=23-{56\over3}-{1\over4}={49\over12}.\cr }$

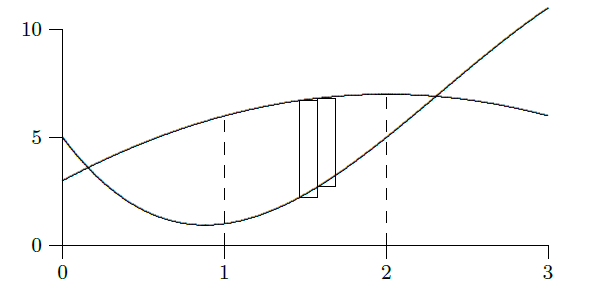
It is worth examining this problem a bit more. We have seen one way to look at it, by viewing the desired area as a big area minus a small area, which leads naturally to the difference between two integrals. But it is instructive to consider how we might find the desired area directly. We can approximate the area by dividing the area into thin sections and approximating the area of each section by a rectangle, as indicated in figure 9.1.2. The area of a typical rectangle is $\Delta x(f(x_i)-g(x_i))$ , so the total area is approximately

$\sum_{i=0}^{n-1} (f(x_i)-g(x_i))\Delta x.$ This is exactly the sort of sum that turns into an integral in the limit, namely the integral

$\int_1^2 f(x)-g(x)\,dx.$ Of course, this is the integral we actually computed above, but we have now arrived at it directly rather than as a modification of the difference between two other integrals. In that example it really doesn't matter which approach we take, but in some cases this second approach is better.

$Approximating area between curves with rectangles.$
Figure 9.1.2. Approximating area between curves with rectangles.

we show the two curves together, with the desired area shaded, then ff alone with the area under ff shaded, and then gg alone with the area under gg shaded.

Area between curves.

Area between curves that cross.

Area bounded by two curves.

Contributors and Attributions

Support Center

How can we help?

we show the two curves together, with the desired area shaded, then $f$ alone with the area under $f$ shaded, and then $g$ alone with the area under $g$ shaded.