15.4: Surface Area

We next seek to compute the area of a surface above (or below) a region in the $xy$ plane. How might we approximate this? We start, as usual, by dividing the region into a grid of small rectangles. We want to approximate the area of the surface above one of these small rectangles. The area is very close to the area of the tangent plane above the small rectangle. If the tangent plane just happened to be horizontal, of course the area would simply be the area of the rectangle. For a typical plane, however, the area is the area of a parallelogram, as indicated in Figure $\PageIndex{1}$. Note that the area of the parallelogram is obviously larger the more "tilted'' the tangent plane. In the interactive figure you can see that viewed from above the four parallelograms exactly cover a rectangular region in the $xy$ plane.

Figure $\PageIndex{1}$: Small parallelograms at points of tangency (AP).

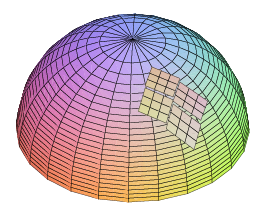
Now recall a curious fact: the area of a parallelogram can be computed as the cross product of two vectors. We simply need to acquire two vectors, parallel to the sides of the parallelogram and with lengths to match. But this is easy: in the $x$ direction we use the tangent vector we already know, namely $\langle 1,0,f_x\rangle$ and multiply by $\Delta x$ to shrink it to the right size: $\langle \Delta x,0,f_x\Delta x\rangle$. In the $y$ direction we do the same thing and get $\langle 0,\Delta y,f_y\Delta y\rangle$. The cross product of these vectors is $\langle f_x,f_y,-1\rangle\,\Delta x\,\Delta y$ with length $\sqrt{f_x^2+f_y^2+1}\,\Delta x\,\Delta y$, the area of the parallelogram. Now we add these up and take the limit, to produce the integral $\int_{x_0}^{x_1}\int_{y_0}^{y_1} \sqrt{f_x^2+f_y^2+1}\,dy\,dx.$ As before, the limits need not be constant.

Example $\PageIndex{1}$

We find the area of the hemisphere $z=\sqrt{1-x^2-y^2}$.

Solution

We compute the derivatives

$$f_x={-x\over\sqrt{1-x^2-y^2}} \qquad f_x={-y\over\sqrt{1-x^2-y^2}},$$

and then the area is

$$\int_{-1}^{1}\int_{-\sqrt{1-x^2}}^{\sqrt{1-x^2}} \sqrt{ {x^2\over1-x^2-y^2}+{y^2\over1-x^2-y^2}+1}\,dy\,dx.$$

This is a bit on the messy side, but we can use polar coordinates:

$$\int_{0}^{2\pi}\int_{0}^{1} \sqrt{ {1\over1-r^2}}\;r\,dr\,d\theta.$$

This integral is improper, since the function is undefined at the limit $1$. We therefore compute

$$\lim_{a\to1^-}\int_{0}^{a} \sqrt{ {1\over1-r^2}}\;r\,dr=\lim_{a\to1^-}-\sqrt{1-a^2}+1=1,$$

using the substitution $u=1-r^2$. Then the area is

$$\int_{0}^{2\pi}1\;d\theta=2\pi.$$

You may recall that the area of a sphere of radius $r$ is $4\pi r^2$, so half the area of a unit sphere is $(1/2)4\pi=2\pi$, in agreement with our answer.

Contributors

• David Guichard (Whitman College)

• Integrated by Justin Marshall.