6.8: Exponential Growth and Decay

Learning Objectives

• Use the exponential growth model in applications, including population growth and compound interest.
• Explain the concept of doubling time.
• Use the exponential decay model in applications, including radioactive decay and Newton’s law of cooling.
• Explain the concept of half-life.

One of the most prevalent applications of exponential functions involves growth and decay models. Exponential growth and decay show up in a host of natural applications. From population growth and continuously compounded interest to radioactive decay and Newton’s law of cooling, exponential functions are ubiquitous in nature. In this section, we examine exponential growth and decay in the context of some of these applications.

Exponential Growth Model

Many systems exhibit exponential growth. These systems follow a model of the form $y=y_0e^{kt},$ where $y_0$ represents the initial state of the system and $k$ is a positive constant, called the growth constant. Notice that in an exponential growth model, we have

$$y′=ky_0e^{kt}=ky. \label{eq1}$$

That is, the rate of growth is proportional to the current function value. This is a key feature of exponential growth. Equation $\ref{eq1}$ involves derivatives and is called a differential equation.

Exponential Growth

Systems that exhibit exponential growth increase according to the mathematical model

$$y=y_0e^{kt} \nonumber$$

where $y_0$ represents the initial state of the system and $k>0$ is a constant, called the growth constant.

Population growth is a common example of exponential growth. Consider a population of bacteria, for instance. It seems plausible that the rate of population growth would be proportional to the size of the population. After all, the more bacteria there are to reproduce, the faster the population grows. Figure $\PageIndex{1}$ and Table $\PageIndex{1}$ represent the growth of a population of bacteria with an initial population of 200 bacteria and a growth constant of 0.02. Notice that after only 2 hours (120 minutes), the population is 10 times its original size!

Figure $\PageIndex{1}$: An example of exponential growth for bacteria.

Table $\PageIndex{1}$: Exponential Growth of a Bacterial Population

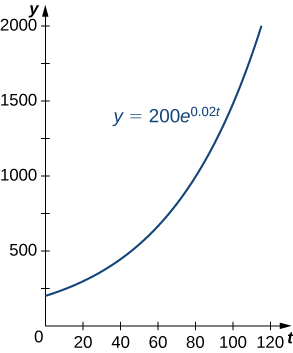
Time(min)	Population Size (no. of bacteria)
10	244
20	298
30	364
40	445
50	544
60	664
70	811
80	991
90	1210
100	1478
110	1805
120	2205

Note that we are using a continuous function to model what is inherently discrete behavior. At any given time, the real-world population contains a whole number of bacteria, although the model takes on noninteger values. When using exponential growth models, we must always be careful to interpret the function values in the context of the phenomenon we are modeling.

Example $\PageIndex{1}$: Population Growth

Consider the population of bacteria described earlier. This population grows according to the function $f(t)=200e^{0.02t},$ where t is measured in minutes. How many bacteria are present in the population after $5$ hours ($300$ minutes)? When does the population reach $100,000$ bacteria?

Solution

We have $f(t)=200e^{0.02t}.$ Then

$$f(300)=200e^{0.02(300)}≈80,686. \nonumber$$

There are $80,686$ bacteria in the population after $5$ hours.

To find when the population reaches $100,000$ bacteria, we solve the equation

$$\begin{align*} 100,000 &= 200e^{0.02t} \\[4pt] 500 &=e^{0.02t} \\[4pt] \ln 500 &=0.02 t \\[4pt] t &=\frac{\ln 500}{0.02}≈310.73. \end{align*} \nonumber$$

The population reaches $100,000$ bacteria after $310.73$ minutes.

Exercise $\PageIndex{1}$

Consider a population of bacteria that grows according to the function $f(t)=500e^{0.05t}$, where $t$ is measured in minutes. How many bacteria are present in the population after 4 hours? When does the population reach $100$ million bacteria?

Answer

Use the process from the previous example.

Answer

There are $81,377,396$ bacteria in the population after $4$ hours. The population reaches $100$ million bacteria after $244.12$ minutes.

Let’s now turn our attention to a financial application: compound interest. Interest that is not compounded is called simple interest. Simple interest is paid once, at the end of the specified time period (usually $1$ year). So, if we put $$1000$ in a savings account earning $2%$ simple interest per year, then at the end of the year we have

$$1000(1+0.02)=$1020. \nonumber$$

Compound interest is paid multiple times per year, depending on the compounding period. Therefore, if the bank compounds the interest every $6$ months, it credits half of the year’s interest to the account after $6$ months. During the second half of the year, the account earns interest not only on the initial $$1000$, but also on the interest earned during the first half of the year. Mathematically speaking, at the end of the year, we have

$$1000 \left(1+\dfrac{0.02}{2}\right)^2=$1020.10. \nonumber$$

Similarly, if the interest is compounded every $4$ months, we have

$$1000 \left(1+\dfrac{0.02}{3}\right)^3=$1020.13, \nonumber$$

and if the interest is compounded daily ($365$ times per year), we have $$1020.20$. If we extend this concept, so that the interest is compounded continuously, after $t$ years we have

$$1000\lim_{n→∞} \left(1+\dfrac{0.02}{n}\right)^{nt}. \nonumber$$

Now let’s manipulate this expression so that we have an exponential growth function. Recall that the number $e$ can be expressed as a limit:

$$e=\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m. \nonumber$$

Based on this, we want the expression inside the parentheses to have the form $(1+1/m)$. Let $n=0.02m$. Note that as $n→∞, m→∞$ as well. Then we get

$$1000\lim_{n→∞}\left(1+\dfrac{0.02}{n}\right)^{nt}=1000\lim_{m→∞}\left(1+\dfrac{0.02}{0.02m}\right)^{0.02mt}=1000\left[\lim_{m→∞}\left(1+\dfrac{1}{m}\right)^m\right]^{0.02t}. \nonumber$$

We recognize the limit inside the brackets as the number $e$. So, the balance in our bank account after $t$ years is given by $1000 e^{0.02t}$. Generalizing this concept, we see that if a bank account with an initial balance of $$P$ earns interest at a rate of $r%$, compounded continuously, then the balance of the account after $t$ years is

$$\text{Balance}\;=Pe^{rt}. \nonumber$$

Example $\PageIndex{2}$: Compound Interest

A 25-year-old student is offered an opportunity to invest some money in a retirement account that pays $5%$ annual interest compounded continuously. How much does the student need to invest today to have $$1$ million when she retires at age $65$? What if she could earn $6%$ annual interest compounded continuously instead?

Solution

We have

$$1,000,000=Pe^{0.05(40)} \nonumber$$

$$P=135,335.28. \nonumber$$

She must invest $$135,335.28$ at $5%$ interest.

If, instead, she is able to earn $6%,$ then the equation becomes

$$1,000,000=Pe^{0.06(40)} \nonumber$$

$$P=90,717.95. \nonumber$$

In this case, she needs to invest only $$90,717.95.$ This is roughly two-thirds the amount she needs to invest at $5%$. The fact that the interest is compounded continuously greatly magnifies the effect of the $1%$ increase in interest rate.

Exercise $\PageIndex{2}$

Suppose instead of investing at age $25\sqrt{b^2−4ac}$, the student waits until age $35$. How much would she have to invest at $5%$? At $6%$?

Hint

Use the process from the previous example.

Answer

At $5%$ interest, she must invest $$223,130.16$. At $6%$ interest, she must invest $$165,298.89.$

If a quantity grows exponentially, the time it takes for the quantity to double remains constant. In other words, it takes the same amount of time for a population of bacteria to grow from $100$ to $200$ bacteria as it does to grow from $10,000$ to $20,000$ bacteria. This time is called the doubling time. To calculate the doubling time, we want to know when the quantity reaches twice its original size. So we have

$$\begin{align*} 2y_0 &=y_0e^{kt} \\[4pt] 2 &=e^{kt} \\[4pt] \ln 2 &=kt \\[4pt] t &=\dfrac{\ln 2}{k}. \end{align*} \nonumber$$

Definition: Doubling Time

If a quantity grows exponentially, the doubling time is the amount of time it takes the quantity to double. It is given by

$$\text{Doubling time}=\dfrac{\ln 2}{k}. \nonumber$$

Example $\PageIndex{3}$: Using the Doubling Time

Assume a population of fish grows exponentially. A pond is stocked initially with $500$ fish. After $6$ months, there are $1000$ fish in the pond. The owner will allow his friends and neighbors to fish on his pond after the fish population reaches $10,000$. When will the owner’s friends be allowed to fish?

Solution

We know it takes the population of fish $6$ months to double in size. So, if $t$ represents time in months, by the doubling-time formula, we have $6=(\ln 2)/k$. Then, $k=(\ln 2)/6$. Thus, the population is given by $y=500e^{((\ln 2)/6)t}$. To figure out when the population reaches $10,000$ fish, we must solve the following equation:

$$\begin{align*} 10,000 &=500e^{(\ln 2/6)t} \\[4pt] 20 &=e^{(\ln 2/6)t} \\[4pt] \ln 20 &=\left(\frac{\ln 2}{6}\right)t \\[4pt] t &=\frac{6(\ln 20)}{\ln 2} \\[4pt] &≈25.93. \end{align*} \nonumber$$

The owner’s friends have to wait $25.93$ months (a little more than $2$ years) to fish in the pond.

Exercise $\PageIndex{3}$

Suppose it takes $9$ months for the fish population in Example $\PageIndex{3}$ to reach $1000$ fish. Under these circumstances, how long do the owner’s friends have to wait?

Hint

Use the process from the previous example.

Answer

$38.90$ months

Exponential Decay Model

Exponential functions can also be used to model populations that shrink (from disease, for example), or chemical compounds that break down over time. We say that such systems exhibit exponential decay, rather than exponential growth. The model is nearly the same, except there is a negative sign in the exponent. Thus, for some positive constant $k$, we have

$$y=y_0e^{−kt}. \nonumber$$

As with exponential growth, there is a differential equation associated with exponential decay. We have

$$y′=−ky_0e^{−kt}=−ky. \nonumber$$

Exponential Decay

Systems that exhibit exponential decay behave according to the model

$$y=y_0e^{−kt}, \nonumber$$

where $y_0$ represents the initial state of the system and $k>0$ is a constant, called the decay constant.

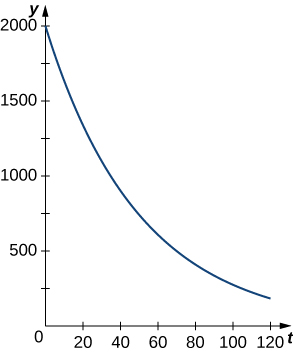
Figure $\PageIndex{2}$ shows a graph of a representative exponential decay function.

Figure $\PageIndex{2}$: An example of exponential decay.

Let’s look at a physical application of exponential decay. Newton’s law of cooling says that an object cools at a rate proportional to the difference between the temperature of the object and the temperature of the surroundings. In other words, if $T$ represents the temperature of the object and $T_a$ represents the ambient temperature in a room, then

$$T′=−k(T−T_a). \nonumber$$

Note that this is not quite the right model for exponential decay. We want the derivative to be proportional to the function, and this expression has the additional $T_a$ term. Fortunately, we can make a change of variables that resolves this issue. Let $y(t)=T(t)−T_a$. Then $y′(t)=T′(t)−0=T′(t)$, and our equation becomes

$$y′=−ky. \nonumber$$

From our previous work, we know this relationship between $y$ and its derivative leads to exponential decay. Thus,

$$y=y_0e^{−kt}, \nonumber$$

and we see that

$$T−T_a=(T_0−T_a)e^{−kt} \nonumber$$

$$T=(T_0−T_a)e^{−kt}+T_a \nonumber$$

where $T_0$ represents the initial temperature. Let’s apply this formula in the following example.

Example $\PageIndex{4}$: Newton’s Law of Cooling

According to experienced baristas, the optimal temperature to serve coffee is between $155°F$ and $175°F$. Suppose coffee is poured at a temperature of $200°F$, and after $2$ minutes in a $70°F$ room it has cooled to $180°F$. When is the coffee first cool enough to serve? When is the coffee too cold to serve? Round answers to the nearest half minute.

Solution

We have

$$\begin{align*} T &=(T_0−T_a)e^{−kt}+T_a \\[4pt] 180 &=(200−70)e^{−k(2)}+70 \\[4pt] 110 &=130e^{−2k} \\[4pt] \dfrac{11}{13} &=e^{−2k} \\[4pt] \ln \dfrac{11}{13} &=−2k \\[4pt] \ln 11−\ln 13 &=−2k \\[4pt] k &=\dfrac{\ln 13−\ln 11}{2} \end{align*}$$

Then, the model is

$$T=130e^{(\ln 11−\ln 13/2)t}+70. \nonumber$$

The coffee reaches $175°F$ when

$$\begin{align*} 175 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt]105 &=130e^{(\ln 11−\ln 13/2)t} \\[4pt] \dfrac{21}{26} &=e^{(\ln 11−\ln 13/2)t} \\[4pt] \ln \dfrac{21}{26} &=\dfrac{\ln 11−\ln 13}{2}t \\[4pt] \ln 21−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 21−\ln 26)}{\ln 11−\ln 13}\\[4pt] &≈2.56. \end{align*}$$

The coffee can be served about $2.5$ minutes after it is poured. The coffee reaches $155°F$ at

$$\begin{align*} 155 &=130e^{(\ln 11−\ln 13/2)t}+70 \\[4pt] 85 &=130e^{(\ln 11−\ln 13)t} \\[4pt] \dfrac{17}{26} &=e^{(\ln 11−\ln 13)t} \\[4pt] \ln 17−\ln 26 &=\left(\dfrac{\ln 11−\ln 13}{2}\right)t \\[4pt] t &=\dfrac{2(\ln 17−\ln 26)}{\ln 11−\ln 13} \\[4pt] &≈5.09.\end{align*}$$

The coffee is too cold to be served about $5$ minutes after it is poured.

Exercise $\PageIndex{4}$

Suppose the room is warmer $(75°F)$ and, after $2$ minutes, the coffee has cooled only to $185°F.$ When is the coffee first cool enough to serve? When is the coffee be too cold to serve? Round answers to the nearest half minute.

Hint

Use the process from the previous example.

Answer

The coffee is first cool enough to serve about $3.5$ minutes after it is poured. The coffee is too cold to serve about $7$ minutes after it is poured.

Just as systems exhibiting exponential growth have a constant doubling time, systems exhibiting exponential decay have a constant half-life. To calculate the half-life, we want to know when the quantity reaches half its original size. Therefore, we have

$\dfrac{y_0}{2}=y_0e^{−kt}$

$\dfrac{1}{2}=e^{−kt}$

$−\ln 2=−kt$

$t=\dfrac{\ln 2}{k}$.

Note: This is the same expression we came up with for doubling time.

Definition: Half-Life

If a quantity decays exponentially, the half-life is the amount of time it takes the quantity to be reduced by half. It is given by

$$\text{Half-life}=\dfrac{\ln 2}{k}. \nonumber$$

Example $\PageIndex{5}$: Radiocarbon Dating

One of the most common applications of an exponential decay model is carbon dating. Carbon-14 decays (emits a radioactive particle) at a regular and consistent exponential rate. Therefore, if we know how much carbon-14 was originally present in an object and how much carbon-14 remains, we can determine the age of the object. The half-life of carbon-14 is approximately 5730 years—meaning, after that many years, half the material has converted from the original carbon-14 to the new nonradioactive nitrogen-14. If we have 100 g carbon-14 today, how much is left in 50 years? If an artifact that originally contained 100 g of carbon-14 now contains 10 g of carbon-14, how old is it? Round the answer to the nearest hundred years.

Solution

We have

$$5730=\dfrac{\ln 2}{k} \nonumber$$

$$k=\dfrac{\ln 2}{5730}.\nonumber$$

So, the model says

$$y=100e^{−(\ln 2/5730)t}.\nonumber$$

In $50$ years, we have

$$y=100e^{−(\ln 2/5730)(50)}≈99.40\nonumber$$

Therefore, in $50$ years, $99.40$ g of carbon-14 remains.

To determine the age of the artifact, we must solve

$$\begin{align*} 10 &=100e^{−(\ln 2/5730)t} \\[4pt] \dfrac{1}{10} &= e^{−(\ln 2/5730)t} \\ t &≈19035. \end{align*}$$

The artifact is about $19,000$ years old.

Exercise $\PageIndex{5}$: Carbon-14 Decay

If we have 100 g of carbon-14 , how much is left after 500 years? If an artifact that originally contained 100 g of carbon-14 now contains 20 g of carbon-14, how old is it? Round the answer to the nearest hundred years.

Hint

Use the process from the previous example.

Answer

A total of 94.13 g of carbon-14 remains after 500 years. The artifact is approximately 13,300 years old.

Key Concepts

• Exponential growth and exponential decay are two of the most common applications of exponential functions.
• Systems that exhibit exponential growth follow a model of the form $y=y_0e^{kt}$.
• In exponential growth, the rate of growth is proportional to the quantity present. In other words, $y′=ky$.
• Systems that exhibit exponential growth have a constant doubling time, which is given by $(\ln 2)/k$.
• Systems that exhibit exponential decay follow a model of the form $y=y_0e^{−kt}.$
• Systems that exhibit exponential decay have a constant half-life, which is given by $(\ln 2)/k.$

Glossary

doubling time

if a quantity grows exponentially, the doubling time is the amount of time it takes the quantity to double, and is given by $(\ln 2)/k$

exponential decay

systems that exhibit exponential decay follow a model of the form $y=y_0e^{−kt}$

exponential growth

systems that exhibit exponential growth follow a model of the form $y=y_0e^{kt}$

half-life

if a quantity decays exponentially, the half-life is the amount of time it takes the quantity to be reduced by half. It is given by $(\ln 2)/k$