7.3: Trigonometric Substitution

Learning Objectives

• Solve integration problems involving the square root of a sum or difference of two squares.

In this section, we explore integrals containing expressions of the form $\sqrt{a^2−x^2}$, $\sqrt{a^2+x^2}$, and $\sqrt{x^2−a^2}$, where the values of $a$ are positive. We have already encountered and evaluated integrals containing some expressions of this type, but many still remain inaccessible. The technique of trigonometric substitution comes in very handy when evaluating these integrals. This technique uses substitution to rewrite these integrals as trigonometric integrals.

Integrals Involving $\sqrt{a^2−x^2}$

Before developing a general strategy for integrals containing $\sqrt{a^2−x^2}$, consider the integral $\displaystyle ∫\textstyle\sqrt{9−x^2}dx.$ This integral cannot be evaluated using any of the techniques we have discussed so far. However, if we make the substitution $x=3\sin θ$, we have $dx=3\cos θ \, dθ.$ After substituting into the integral, we have

$$∫\sqrt{9−x^2}\,dx=∫\textstyle\sqrt{ 9−(3\sin θ)^2}\cdot 3\cos θ \,dθ. \nonumber$$

After simplifying, we have

$$∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{1−\sin^2θ}\cdot\cos θ \, dθ. \nonumber$$

Letting $1−\sin^2θ=\cos^2θ,$ we now have

$$∫\sqrt{ 9−x^2}\,dx=∫ 9\textstyle\sqrt{\cos^2θ}\cos θ \, dθ. \nonumber$$

Assuming that $\cos θ≥0$, we have

$$∫\textstyle\sqrt{ 9−x^2}\,dx=∫ 9\cos^2θ \, dθ. \nonumber$$

At this point, we can evaluate the integral using the techniques developed for integrating powers and products of trigonometric functions. Before completing this example, let’s take a look at the general theory behind this idea.

To evaluate integrals involving $\sqrt{a^2−x^2}$, we make the substitution $x=a\sin θ$ and $dx=a\cos θ$. To see that this actually makes sense, consider the following argument: The domain of $\sqrt{a^2−x^2}$ is $[−a,a]$. Thus,

$$−a≤x≤a. \nonumber$$

Consequently,

$$−1≤\dfrac{x}{a}≤1. \nonumber$$

Since the range of $\sin x$ over $[−(π/2),π/2]$ is $[−1,1]$, there is a unique angle $θ$ satisfying $−(π/2)≤θ≤π/2$ so that $\sin θ=x/a$, or equivalently, so that $x=a\sin θ$. If we substitute $x=a\sin θ$ into $\sqrt{a^2−x^2}$, we get

$$\begin{align*} \sqrt{a^2−x^2} &= \sqrt{a^2−(a\sin θ)^2} & & \text{Let }x=a\sin θ\text{ where }−\dfrac{π}{2}≤θ≤\dfrac{π}{2}.\\[4pt] & & & \text{Simplify.} \\[4pt] &=\sqrt{a^2−a^2\sin^2θ} & & \text{Factor out }a^2. \\[4pt] &=\sqrt{a^2(1−\sin^2θ)} & & \text{Substitute }1−\sin^2x=\cos^2x.\\[4pt] &=\sqrt{a^2\cos^2θ} & & \text{Take the square root.}\\[4pt] &=|a\cos θ| \\[4pt] &=a\cos θ \end{align*}$$

Since $\cos x≥0$ on $−\dfrac{π}{2}≤θ≤\dfrac{π}{2}$ and $a>0, |a\cos θ|=a\cos θ.$ We can see, from this discussion, that by making the substitution $x=a\sin θ$, we are able to convert an integral involving a radical into an integral involving trigonometric functions. After we evaluate the integral, we can convert the solution back to an expression involving $x$. To see how to do this, let’s begin by assuming that $0<x<a$. In this case, $0<θ<\dfrac{π}{2}$. Since $\sin θ=\dfrac{x}{a}$, we can draw the reference triangle in Figure $\PageIndex{1}$ to assist in expressing the values of $\cos θ, \, \tan θ,$ and the remaining trigonometric functions in terms of $x$. It can be shown that this triangle actually produces the correct values of the trigonometric functions evaluated at $θ$ for all $θ$ satisfying $−\dfrac{π}{2}≤θ≤\dfrac{π}{2}$. It is useful to observe that the expression $\sqrt{a^2−x^2}$ actually appears as the length of one side of the triangle. Last, should $θ$ appear by itself, we use $θ=\sin^{−1}\left(\dfrac{x}{a}\right).$

Figure $\PageIndex{1}$: A reference triangle can help express the trigonometric functions evaluated at $θ$ in terms of $x$.

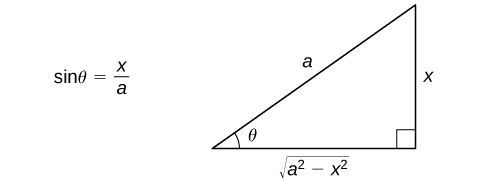
The essential part of this discussion is summarized in the following problem-solving strategy.

Problem-Solving Strategy: Integrating Expressions Involving $\sqrt{a^2−x^2}$

1. It is a good idea to make sure the integral cannot be evaluated easily in another way. For example, although this method can be applied to integrals of the form $\displaystyle ∫\dfrac{1}{\sqrt{a^2−x^2}}dx$, $\displaystyle ∫\dfrac{x}{\sqrt{a^2−x^2}}dx,$ and $\displaystyle ∫x\sqrt{a^2−x^2}\,dx,$ they can each be integrated directly either by formula or by a simple $u$-substitution.
2. Make the substitution $x=a \sin θ$ and $dx=a\cos θ \,dθ.$ Note: This substitution yields $\sqrt{a^2−x^2}=a\cos θ.$
3. Simplify the expression.
4. Evaluate the integral using techniques from the section on trigonometric integrals.
5. Use the reference triangle from Figure 1 to rewrite the result in terms of $x$. You may also need to use some trigonometric identities and the relationship $θ=\sin^{−1}\left(\dfrac{x}{a}\right).$

The following example demonstrates the application of this problem-solving strategy.

Example $\PageIndex{1}$: Integrating an Expression Involving $\sqrt{a^2−x^2}$

Evaluate

$$∫\sqrt{ 9−x^2}dx. \nonumber$$

Solution

Begin by making the substitutions $x=3\sin θ$ and $dx=3\cos θ \, dθ.$ Since $\sin θ=\dfrac{x}{3}$, we can construct the reference triangle shown in Figure 2.

Figure $\PageIndex{2}$: A reference triangle can be constructed for Example $\PageIndex{1}$.

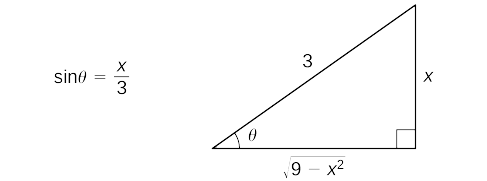
Thus,

$\displaystyle ∫\sqrt{9−x^2}\,dx=∫\sqrt{ 9−(3\sin θ)^2}3\cos θ\,dθ$  Substitute $x=3\sin θ$ and $dx=3\cos θ \,dθ$.

$=∫\sqrt{ 9(1−\sin^2θ)}\cdot 3\cos θ \, dθ$ Simplify.

$=∫\sqrt{ 9\cos^2θ}\cdot 3\cos θ \, dθ$ Substitute $\cos^2θ=1−\sin^2θ$.

$=∫ 3|\cos θ|3\cos θ \, dθ$ Take the square root.

$=∫ 9\cos^2θ \, dθ$ Simplify. Since $−\dfrac{π}{2}≤θ≤\dfrac{π}{2},\cos θ≥0$ and $|\cos θ|=\cos θ.$

$=∫ 9\left(\dfrac{1}{2}+\dfrac{1}{2}\cos(2θ)\right)\,dθ$ Use the strategy for integrating an even power of $\cos θ$.

$=\dfrac{9}{2}θ+\dfrac{9}{4}\sin(2θ)+C$ Evaluate the integral.

$=\dfrac{9}{2}θ+\dfrac{9}{4}(2\sin θ\cos θ)+C$  Substitute $\sin(2θ)=2\sin θ\cos θ$.

$=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{9}{2}⋅\dfrac{x}{3}⋅\dfrac{\sqrt{9−x^2}}{3}+C$ Substitute $\sin^{−1}\left(\dfrac{x}{3}\right)=θ$ and $\sin θ=\frac{x}{3}$.

Use the reference triangle to see that $\cos θ=\dfrac{\sqrt{9−x^2}}{3}$and make this substitution. Simplify.

$=\dfrac{9}{2}\sin^{−1}\left(\dfrac{x}{3}\right)+\dfrac{x\sqrt{9−x^2}}{2}+C.$ Simplify.

Example $\PageIndex{2}$: Integrating an Expression Involving $\sqrt{a^2−x^2}$

Evaluate

$$∫\dfrac{\sqrt{4−x^2}}{x}dx. \nonumber$$

Solution

First make the substitutions $x=2\sin θ$ and $dx=2\cos θ\,dθ$. Since $\sin θ=\dfrac{x}{2}$, we can construct the reference triangle shown in Figure $\PageIndex{3}$.

Figure $\PageIndex{3}$: A reference triangle can be constructed for Example $\PageIndex{2}$.

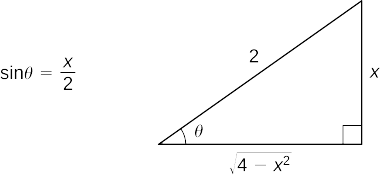
Thus,

$\displaystyle ∫\dfrac{\sqrt{4−x^2}}{x}dx=∫\dfrac{\sqrt{4−(2\sin θ)^2}}{2\sin θ}2\cos θ \, dθ$ Substitute $x=2\sin θ$ and $dx=2\cos θ\,dθ.$

$=∫\dfrac{2\cos^2θ}{\sin θ}\,dθ$ Substitute $\cos^2θ=1−\sin^2θ$ and simplify.

$=∫\dfrac{2(1−\sin^2θ)}{\sin θ}\,dθ$ Substitute $\cos^2θ=1−\sin^2θ$.

$=∫ (2\csc θ−2\sin θ)\,dθ$ Separate the numerator, simplify, and use $\csc θ=\dfrac{1}{\sin θ}$.

$=2 \ln |\csc θ−\cot θ|+2\cos θ+C$ Evaluate the integral.

$=2 \ln \left|\dfrac{2}{x}−\dfrac{\sqrt{4−x^2}}{x}\right|+\sqrt{4−x^2}+C.$ Use the reference triangle to rewrite the expression in terms of $x$ and simplify.

In the next example, we see that we sometimes have a choice of methods.

Example $\PageIndex{3}$: Integrating an Expression Involving $\sqrt{a^2−x^2}$ Two Ways

Evaluate $∫ x^3\sqrt{1−x^2}dx$ two ways: first by using the substitution $u=1−x^2$ and then by using a trigonometric substitution.

Method 1

Let $u=1−x^2$ and hence $x^2=1−u$. Thus, $du=−2x\,dx.$ In this case, the integral becomes

$∫ x^3\sqrt{1−x^2}\,dx=−\dfrac{1}{2}∫ x^2\sqrt{1−x^2}(−2x\,dx)$ Make the substitution.

$=−\dfrac{1}{2}∫ (1−u)\sqrt{u}\,du$ Expand the expression.

$=−\dfrac{1}{2}∫(u^{1/2}−u^{3/2})\,du$ Evaluate the integral.

$=−\dfrac{1}{2}(\dfrac{2}{3}u^{3/2}−\dfrac{2}{5}u^{5/2})+C$ Rewrite in terms of x.

$=−\dfrac{1}{3}(1−x^2)^{3/2}+\dfrac{1}{5}(1−x^2)^{5/2}+C.$

Method 2

Let $x=\sin θ$. In this case, $dx=\cos θ \, dθ.$ Using this substitution, we have

$∫ x^3\sqrt{1−x^2}dx=∫ \sin^3θ\cos^2θ \, dθ$

$=∫ (1−\cos^2θ)\cos^2θ\sin θ \, dθ$ Let $u=\cos θ$. Thus,$du=−\sin θ \, dθ.$

$=∫ (u^4−u^2)\,du$

$=\dfrac{1}{5}u^5−\dfrac{1}{3}u^3+C$ Substitute $\cos θ=u.$

$=\dfrac{1}{5}\cos^5θ−\dfrac{1}{3}\cos^3θ+C$ Use a reference triangle to see that $\cos θ=\sqrt{1−x^2}.$

$=\dfrac{1}{5}(1−x^2)^{5/2}−\dfrac{1}{3}(1−x^2)^{3/2}+C.$

Exercise $\PageIndex{1}$

Rewrite the integral $\displaystyle ∫\dfrac{x^3}{\sqrt{25−x^2}}\,dx$ using the appropriate trigonometric substitution (do not evaluate the integral).

Hint

Substitute $x=5\sin θ$ and $dx=5\cos θ \, dθ.$

Answer

$\displaystyle ∫ 125\sin^3θ \, dθ$

Integrating Expressions Involving $\sqrt{a^2+x^2}$

For integrals containing $\sqrt{a^2+x^2}$,let’s first consider the domain of this expression. Since $\sqrt{a^2+x^2}$ is defined for all real values of $x$, we restrict our choice to those trigonometric functions that have a range of all real numbers. Thus, our choice is restricted to selecting either $x=a\tan θ$ or $x=a\cot θ$. Either of these substitutions would actually work, but the standard substitution is $x=a\tan θ$ or, equivalently, $\tan θ=x/a$. With this substitution, we make the assumption that $−(π/2)<θ<π/2$, so that we also have $θ=\tan^{−1}(x/a).$ The procedure for using this substitution is outlined in the following problem-solving strategy.

Problem-Solving Strategy: Integrating Expressions Involving $\sqrt{a^2+x^2}$

1. Check to see whether the integral can be evaluated easily by using another method. In some cases, it is more convenient to use an alternative method.
2. Substitute $x=a\tan θ$ and $dx=a\sec^2θ \, dθ.$ This substitution yields $\sqrt{a^2+x^2}=\sqrt{a^2+(a\tan θ)^2}=\sqrt{a^2(1+\tan^2θ)}=\sqrt{a^2sec^2θ}=|a\sec θ|=a\sec θ.$ (Since $−\dfrac{π}{2}<θ<\dfrac{π}{2}$ and $\sec θ>0$ over this interval, $|a\sec θ|=a\sec θ$.)
3. Simplify the expression.
4. Evaluate the integral using techniques from the section on trigonometric integrals.
5. Use the reference triangle from Figure $\PageIndex{4}$ to rewrite the result in terms of $x$. You may also need to use some trigonometric identities and the relationship $θ=\tan^{−1}\left(\dfrac{x}{a}\right)$. (Note: The reference triangle is based on the assumption that $x>0$; however, the trigonometric ratios produced from the reference triangle are the same as the ratios for which $x≤0$.)

Figure $\PageIndex{4}$: A reference triangle can be constructed to express the trigonometric functions evaluated at $θ$ in terms of $x$.

Example $\PageIndex{4}$: Integrating an Expression Involving $\sqrt{a^2+x^2}$

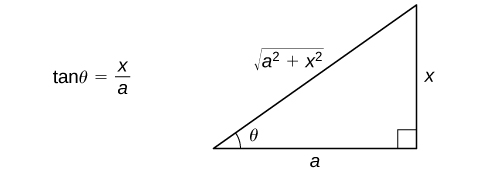
Evaluate $\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}$ and check the solution by differentiating.

Solution

Begin with the substitution $x=\tan θ$ and $dx=sec^2θ\,dθ$. Since $\tan θ=x$, draw the reference triangle in Figure $\PageIndex{5}$.

Figure $\PageIndex{5}$: The reference triangle for Example $\PageIndex{4}$.

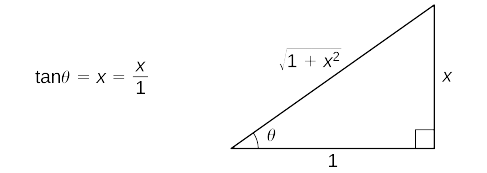
Thus,

$\displaystyle \begin{align*} ∫\dfrac{dx}{\sqrt{1+x^2}} &=∫\dfrac{\sec^2θ}{\sec θ}dθ & & \text{Substitute }x=\tan θ\text{ and }dx=\sec^2θ \, dθ. \\[4pt] & & &\text{This substitution makes }\sqrt{1+x^2}=\sec θ.\text{ Simplify.} \\[4pt] &=∫ \sec θ \, dθ & & \text{Evaluate the integral.} \\[4pt] &= \ln |\sec θ+\tan θ|+C & & \text{Use the reference triangle to express the result in terms of }x. \\[4pt] &= \ln |\sqrt{1+x^2}+x|+C \end{align*}$

To check the solution, differentiate:

$\dfrac{d}{dx}\Big( \ln |\sqrt{1+x^2}+x|\Big)=\dfrac{1}{\sqrt{1+x^2}+x}⋅\left(\dfrac{x}{\sqrt{1+x^2}}+1\right) =\dfrac{1}{\sqrt{1+x^2}+x}⋅\dfrac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}.$

Since $\sqrt{1+x^2}+x>0$ for all values of $x$, we could rewrite $\ln |\sqrt{1+x^2}+x|+C= \ln (\sqrt{1+x^2}+x)+C$, if desired.

Example $\PageIndex{5}$: Evaluating $∫\dfrac{dx}{\sqrt{1+x^2}}$ Using a Different Substitution

Use the substitution $x=\sinh θ$ to evaluate $\displaystyle ∫\dfrac{dx}{\sqrt{1+x^2}}.$

Solution

Because $\sinh θ$ has a range of all real numbers, and $1+\sinh^2θ=\cosh^2θ$, we may also use the substitution $x=\sinh θ$ to evaluate this integral. In this case, $dx=\cosh θ \,dθ.$ Consequently,

$\displaystyle \begin{align*} ∫\dfrac{dx}{\sqrt{1+x^2}}&=∫\dfrac{\cosh θ}{\sqrt{1+\sinh^2θ}}dθ & & \text{Substitute }x=\sinh θ\text{ and }dx=\cosh θ \, dθ.\\[4pt] & & & \text{Substitute }1+\sinh^2θ=\cosh^2θ. \\[4pt] &=∫\dfrac{\cosh θ}{\sqrt{\cosh^2θ}}dθ & & \text{Since }\sqrt{\cosh^2θ}=|\cosh θ| \\[4pt] &=∫\dfrac{\cosh θ}{|\cosh θ|}dθ & & |\cosh θ|=\cosh θ\text{ since }\cosh θ>0\text{ for all }θ.\\[4pt] &=∫\dfrac{\cosh θ}{\cosh θ}dθ & & \text{Simplify.} \\[4pt] &=∫ 1\,dθ & & \text{Evaluate the integral.} \\[4pt] &=θ+C & & \text{Since }x=\sinh θ,\text{ we know }θ=\sinh^{−1}x. \\[4pt] &=\sinh^{−1}x+C. \end{align*}$

Analysis

This answer looks quite different from the answer obtained using the substitution $x=\tan θ.$ To see that the solutions are the same, set $y=\sinh^{−1}x$. Thus, $\sinh y=x.$ From this equation we obtain:

$$\dfrac{e^y−e^{−y}}{2}=x. \nonumber$$

After multiplying both sides by $2e^y$ and rewriting, this equation becomes:

$$e^{2y}−2xe^y−1=0. \nonumber$$

Use the quadratic equation to solve for $e^y$:

$$e^y=\dfrac{2x±\sqrt{4x^2+4}}{2}. \nonumber$$

Simplifying, we have:

$$e^y=x±\sqrt{x^2+1}. \nonumber$$

Since $x−\sqrt{x^2+1}<0$, it must be the case that $e^y=x+\sqrt{x^2+1}$. Thus,

$$y= \ln (x+\sqrt{x^2+1}). \nonumber$$

Last, we obtain

$$\sinh^{−1}x= \ln (x+\sqrt{x^2+1}). \nonumber$$

After we make the final observation that, since $x+\sqrt{x^2+1}>0,$

$$\ln (x+\sqrt{x^2+1})= \ln ∣\sqrt{1+x^2}+x∣, \nonumber$$

we see that the two different methods produced equivalent solutions.

Example $\PageIndex{6}$: Finding an Arc Length

Find the length of the curve $y=x^2$ over the interval $[0,\dfrac{1}{2}]$.

Solution

Because $\dfrac{dy}{dx}=2x$, the arc length is given by

$$∫^{1/2}_0\sqrt{1+(2x)^2}dx=∫^{1/2}_0\sqrt{1+4x^2}dx. \nonumber$$

To evaluate this integral, use the substitution $x=\dfrac{1}{2}\tan θ$ and $dx=\tfrac{1}{2}\sec^2θ \, dθ$. We also need to change the limits of integration. If $x=0$, then $θ=0$ and if $x=\dfrac{1}{2}$, then $θ=\dfrac{π}{4}.$ Thus,

$∫^{1/2}_0\sqrt{1+4x^2}dx=∫^{π/4}_0\sqrt{1+\tan^2θ}\cdot \tfrac{1}{2}\sec^2θ \, dθ$ After substitution,$\sqrt{1+4x^2}=\sec θ$. (Substitute $1+\tan^2θ=\sec^2θ$ and simplify.)

$=\tfrac{1}{2}∫^{π/4}_0\sec^3θ \, dθ$ We derived this integral in the previous section.

$=\tfrac{1}{2}(\dfrac{1}{2}\sec θ\tan θ+ \dfrac{1}{2}\ln |\sec θ+\tan θ|)∣^{π/4}_0$ Evaluate and simplify.

$=\tfrac{1}{4}(\sqrt{2}+ \ln (\sqrt{2}+1)).$

Exercise $\PageIndex{2}$

Rewrite $\displaystyle ∫ x^3\sqrt{x^2+4}dx$ by using a substitution involving $\tan θ$.

Hint

Use $x=2\tan θ$ and $dx=2\sec^2θ \, dθ.$

Answer

$$∫ 32\tan^3θ\sec^3θ \, dθ \nonumber$$

Integrating Expressions Involving $\sqrt{x^2−a^2}$

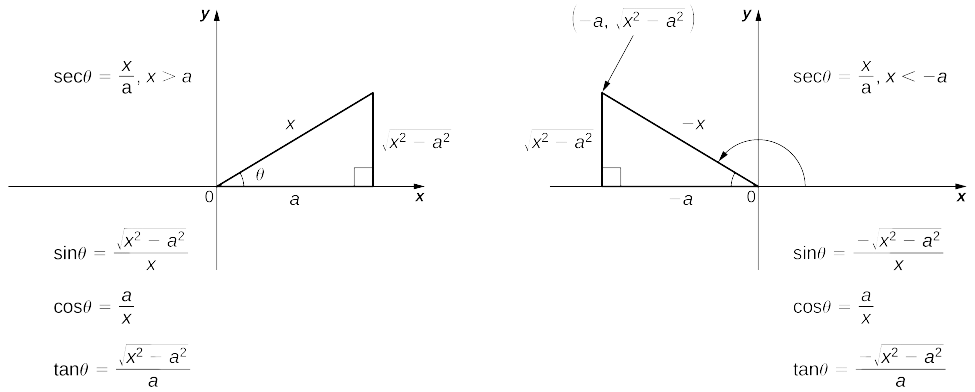
The domain of the expression $\sqrt{x^2−a^2}$ is $(−∞,−a]∪[a,+∞)$. Thus, either $x\le −a$ or $x\ge a.$ Hence, $\dfrac{x}{a}≤−1$ or $\dfrac{x}{a}≥1$. Since these intervals correspond to the range of $\sec θ$ on the set $[0,\dfrac{π}{2})∪(\dfrac{π}{2},π]$, it makes sense to use the substitution $\sec θ=\dfrac{x}{a}$ or, equivalently, $x=a\sec θ$, where $0≤θ<\dfrac{π}{2}$ or $\dfrac{π}{2}<θ≤π$. The corresponding substitution for $dx$ is $dx=a\sec θ\tan θ \, dθ$. The procedure for using this substitution is outlined in the following problem-solving strategy.

Problem-Solving Strategy: Integrals Involving $\sqrt{x^2−a^2}$

1. Check to see whether the integral cannot be evaluated using another method. If so, we may wish to consider applying an alternative technique.
2. Substitute $x=a\sec θ$ and $dx=a\sec θ\tan θ \, dθ$. This substitution yields $$\sqrt{x^2−a^2}=\sqrt{(a\sec θ)^2−a^2}=\sqrt{a^2(\sec^2θ-1)}=\sqrt{a^2\tan^2θ}=|a\tan θ|. \nonumber$$ For $x≥a, |a\tan θ|=a\tan θ$ and for $x≤−a, |a\tan θ|=−a\tan θ.$
3. Simplify the expression.
4. Evaluate the integral using techniques from the section on trigonometric integrals.
5. Use the reference triangles from Figure $\PageIndex{6}$ to rewrite the result in terms of $x$.
6. You may also need to use some trigonometric identities and the relationship $θ=\sec^{−1}\left(\dfrac{x}{a}\right)$. (Note: We need both reference triangles, since the values of some of the trigonometric ratios are different depending on whether $x>a$ or $x<−a$.)

Figure $\PageIndex{6}$: Use the appropriate reference triangle to express the trigonometric functions evaluated at $θ$ in terms of $x$.

Example $\PageIndex{7}$: Finding the Area of a Region

Find the area of the region between the graph of $f(x)=\sqrt{x^2−9}$ and the x-axis over the interval $[3,5].$

Solution

First, sketch a rough graph of the region described in the problem, as shown in the following figure.

Figure $\PageIndex{7}$: Calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution.

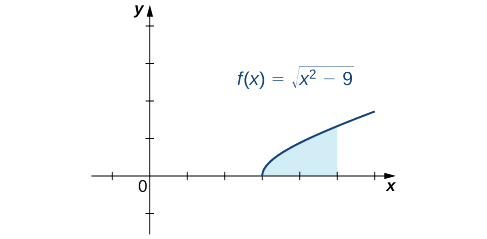
We can see that the area is $A=∫^5_3\sqrt{x^2−9}dx$. To evaluate this definite integral, substitute $x=3\sec θ$ and $dx=3\sec θ\tan θ \, dθ$. We must also change the limits of integration. If $x=3$, then $3=3\sec θ$ and hence $θ=0$. If $x=5$, then $θ=\sec^{−1}(\dfrac{5}{3})$. After making these substitutions and simplifying, we have

Area$=∫^5_3\sqrt{x^2−9}dx$

$=∫^{\sec^{−1}(5/3)}_09\tan^2θ\sec θ \, dθ$ Use $\tan^2θ=\sec^2θ - 1.$

$=∫^{\sec^{−1}(5/3)}_09(\sec^2θ−1)\sec θ \, dθ$ Expand.

$=∫^{\sec^{−1}(5/3)}_09(\sec^3θ−\sec θ)\,dθ$ Evaluate the integral.

$=(\dfrac{9}{2} \ln |\sec θ+\tan θ|+\dfrac{9}{2}\sec θ\tan θ)−9 \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0$ Simplify.

$=\dfrac{9}{2}\sec θ\tan θ−\dfrac{9}{2} \ln |\sec θ+\tan θ|∣^{\sec^{−1}(5/3)}_0$ Evaluate. Use $\sec(\sec^{−1}\dfrac{5}{3})=\dfrac{5}{3}$ and $\tan(\sec^{−1}\dfrac{5}{3})=\dfrac{4}{3}.$

$=\dfrac{9}{2}⋅\dfrac{5}{3}⋅\dfrac{4}{3}−\dfrac{9}{2} \ln ∣\dfrac{5}{3}+\dfrac{4}{3}∣−(\dfrac{9}{2}⋅1⋅0−\dfrac{9}{2} \ln |1+0|)$

$=10−\dfrac{9}{2} \ln 3$

Exercise $\PageIndex{3}$

Evaluate $$∫\dfrac{dx}{\sqrt{x^2−4}}. \nonumber$$ Assume that $x>2.$

Hint

Substitute $x=2\sec θ$ and $dx=2\sec θ\tan θ \, dθ.$

Answer

$$\ln |\dfrac{x}{2}+\dfrac{\sqrt{x^2−4}}{2}|+C \nonumber$$

Key Concepts

• For integrals involving $\sqrt{a^2−x^2}$, use the substitution $x=a\sin θ$ and $dx=a\cos θ \, dθ.$
• For integrals involving $\sqrt{a^2+x^2}$, use the substitution $x=a\tan θ$ and $dx=a\sec^2θ \, dθ$.
• For integrals involving $\sqrt{x^2−a^2}$, substitute $x=a\sec θ$ and $dx=a\sec θ\tan θ \,dθ$.

Glossary

trigonometric substitution

an integration technique that converts an algebraic integral containing expressions of the form $\sqrt{a^2−x^2}$, $\sqrt{a^2+x^2}$, or $\sqrt{x^2−a^2}$ into a trigonometric integral