14.8: Lagrange Multipliers

Learning Objectives

• Use the method of Lagrange multipliers to solve optimization problems with one constraint.
• Use the method of Lagrange multipliers to solve optimization problems with two constraints.

Solving optimization problems for functions of two or more variables can be similar to solving such problems in single-variable calculus. However, techniques for dealing with multiple variables allow us to solve more varied optimization problems for which we need to deal with additional conditions or constraints. In this section, we examine one of the more common and useful methods for solving optimization problems with constraints.

Lagrange Multipliers

In the previous section, an applied situation was explored involving maximizing a profit function, subject to certain constraints. In that example, the constraints involved a maximum number of golf balls that could be produced and sold in \(1\) month \((x),\) and a maximum number of advertising hours that could be purchased per month \((y)\). Suppose these were combined into a single budgetary constraint, such as \(20x+4y≤216\), that took into account both the cost of producing the golf balls and the number of advertising hours purchased per month. The goal is still to maximize profit, but now there is a different type of constraint on the values of \(x\) and \(y\). This constraint and the corresponding profit function

\[f(x,y)=48x+96y−x^2−2xy−9y^2 \nonumber \]

is an example of an optimization problem, and the function \(f(x,y)\) is called the objective function. A graph of various level curves of the function \(f(x,y)\) follows.

Figure \(\PageIndex{1}\): Graph showing level curves of the function \(f(x,y)=48x+96y−x^2−2xy−9y^2\) corresponding to \(c=150,250,350,\) and \(400.\)

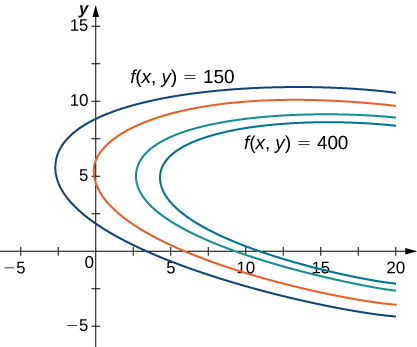
In Figure \(\PageIndex{1}\), the value \(c\) represents different profit levels (i.e., values of the function \(f\)). As the value of \(c\) increases, the curve shifts to the right. Since our goal is to maximize profit, we want to choose a curve as far to the right as possible. If there were no restrictions on the number of golf balls the company could produce or the number of units of advertising available, then we could produce as many golf balls as we want, and advertise as much as we want, and there would be not be a maximum profit for the company. Unfortunately, we have a budgetary constraint that is modeled by the inequality \(20x+4y≤216.\) To see how this constraint interacts with the profit function, Figure \(\PageIndex{2}\) shows the graph of the line \(20x+4y=216\) superimposed on the previous graph.

Figure \(\PageIndex{2}\): Graph of level curves of the function \(f(x,y)=48x+96y−x^2−2xy−9y^2\) corresponding to \(c=150,250,350,\) and \(395\). The red graph is the constraint function.

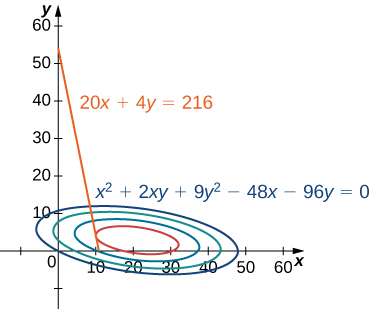
As mentioned previously, the maximum profit occurs when the level curve is as far to the right as possible. However, the level of production corresponding to this maximum profit must also satisfy the budgetary constraint, so the point at which this profit occurs must also lie on (or to the left of) the red line in Figure \(\PageIndex{2}\). Inspection of this graph reveals that this point exists where the line is tangent to the level curve of \(f\). Trial and error reveals that this profit level seems to be around \(395\), when \(x\) and \(y\) are both just less than \(5\). We return to the solution of this problem later in this section. From a theoretical standpoint, at the point where the profit curve is tangent to the constraint line, the gradient of both of the functions evaluated at that point must point in the same (or opposite) direction. Recall that the gradient of a function of more than one variable is a vector. If two vectors point in the same (or opposite) directions, then one must be a constant multiple of the other. This idea is the basis of the method of Lagrange multipliers.

Method of Lagrange Multipliers: One Constraint

Theorem \(\PageIndex{1}\): Let \(f\) and \(g\) be functions of two variables with continuous partial derivatives at every point of some open set containing the smooth curve \(g(x,y)=0.\) Suppose that \(f\), when restricted to points on the curve \(g(x,y)=0\), has a local extremum at the point \((x_0,y_0)\) and that \(\vecs ∇g(x_0,y_0)≠0\). Then there is a number \(λ\) called a Lagrange multiplier, for which

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0). \nonumber \]

Proof

Assume that a constrained extremum occurs at the point \((x_0,y_0).\) Furthermore, we assume that the equation \(g(x,y)=0\) can be smoothly parameterized as

\(x=x(s) \; \text{and}\; y=y(s)\)

where \(s\) is an arc length parameter with reference point \((x_0,y_0)\) at \(s=0\). Therefore, the quantity \(z=f(x(s),y(s))\) has a relative maximum or relative minimum at \(s=0\), and this implies that \(\dfrac{dz}{ds}=0\) at that point. From the chain rule,

\[\begin{align*} \dfrac{dz}{ds} &=\dfrac{∂f}{∂x}⋅\dfrac{∂x}{∂s}+\dfrac{∂f}{∂y}⋅\dfrac{∂y}{∂s} \\[4pt] &=\left(\dfrac{∂f}{∂x}\hat{\mathbf i}+\dfrac{∂f}{∂y}\hat{\mathbf j}\right)⋅\left(\dfrac{∂x}{∂s}\hat{\mathbf i}+\dfrac{∂y}{∂s}\hat{\mathbf j}\right)\\[4pt] &=0, \end{align*}\]

where the derivatives are all evaluated at \(s=0\). However, the first factor in the dot product is the gradient of \(f\), and the second factor is the unit tangent vector \(\vec{\mathbf T}(0)\) to the constraint curve. Since the point \((x_0,y_0)\) corresponds to \(s=0\), it follows from this equation that

\[\vecs ∇f(x_0,y_0)⋅\vecs{\mathbf T}(0)=0, \nonumber \]

which implies that the gradient is either the zero vector \(\vecs 0\) or it is normal to the constraint curve at a constrained relative extremum. However, the constraint curve \(g(x,y)=0\) is a level curve for the function \(g(x,y)\) so that if \(\vecs ∇g(x_0,y_0)≠0\) then \(\vecs ∇g(x_0,y_0)\) is normal to this curve at \((x_0,y_0)\) It follows, then, that there is some scalar \(λ\) such that

\[\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0) \nonumber \]

\(\square\)

To apply Theorem \(\PageIndex{1}\) to an optimization problem similar to that for the golf ball manufacturer, we need a problem-solving strategy.

Problem-Solving Strategy: Steps for Using Lagrange Multipliers

1. Determine the objective function \(f(x,y)\) and the constraint function \(g(x,y).\) Does the optimization problem involve maximizing or minimizing the objective function?
2. Set up a system of equations using the following template: \[\begin{align} \vecs ∇f(x_0,y_0) &=λ\vecs ∇g(x_0,y_0) \\[4pt] g(x_0,y_0) &=0 \end{align}. \nonumber \]
3. Solve for \(x_0\) and \(y_0\).
4. The largest of the values of \(f\) at the solutions found in step \(3\) maximizes \(f\); the smallest of those values minimizes \(f\).

Example \(\PageIndex{1}\): Using Lagrange Multipliers

Use the method of Lagrange multipliers to find the minimum value of \(f(x,y)=x^2+4y^2−2x+8y\) subject to the constraint \(x+2y=7.\)

Solution

Let’s follow the problem-solving strategy:

1. The objective function is \(f(x,y)=x^2+4y^2−2x+8y.\) To determine the constraint function, we must first subtract \(7\) from both sides of the constraint. This gives \(x+2y−7=0.\) The constraint function is equal to the left-hand side, so \(g(x,y)=x+2y−7\). The problem asks us to solve for the minimum value of \(f\), subject to the constraint (Figure \(\PageIndex{3}\)).

Figure \(\PageIndex{3}\): Graph of level curves of the function \(f(x,y)=x^2+4y^2−2x+8y\) corresponding to \(c=10\) and \(26\). The red graph is the constraint function.

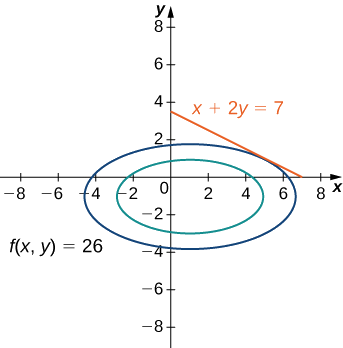
2. We then must calculate the gradients of both \(f\) and \(g\):

\[\begin{align*} \vecs \nabla f \left( x, y \right) &= \left( 2x - 2 \right) \hat{\mathbf{i}} + \left( 8y + 8 \right) \hat{\mathbf{j}} \\ \vecs \nabla g \left( x, y \right) &= \hat{\mathbf{i}} + 2 \hat{\mathbf{j}}. \end{align*}\]

The equation \(\vecs \nabla f \left( x_0, y_0 \right) = \lambda \vecs \nabla g \left( x_0, y_0 \right)\) becomes

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \left( \hat{\mathbf{i}} + 2 \hat{\mathbf{j}} \right), \nonumber \]

which can be rewritten as

\[\left( 2 x_0 - 2 \right) \hat{\mathbf{i}} + \left( 8 y_0 + 8 \right) \hat{\mathbf{j}} = \lambda \hat{\mathbf{i}} + 2 \lambda \hat{\mathbf{j}}. \nonumber \]

Next, we set the coefficients of \(\hat{\mathbf{i}}\) and \(\hat{\mathbf{j}}\) equal to each other:

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda. \end{align*}\]

The equation \(g \left( x_0, y_0 \right) = 0\) becomes \(x_0 + 2 y_0 - 7 = 0\). Therefore, the system of equations that needs to be solved is

\[\begin{align*} 2 x_0 - 2 &= \lambda \\ 8 y_0 + 8 &= 2 \lambda \\ x_0 + 2 y_0 - 7 &= 0. \end{align*}\]

3. This is a linear system of three equations in three variables. We start by solving the second equation for \(λ\) and substituting it into the first equation. This gives \(λ=4y_0+4\), so substituting this into the first equation gives \[2x_0−2=4y_0+4.\nonumber \] Solving this equation for \(x_0\) gives \(x_0=2y_0+3\). We then substitute this into the third equation:

\[\begin{align*} (2y_0+3)+2y_0−7 =0 \\[4pt]4y_0−4 =0 \\[4pt]y_0 =1. \end{align*}\]

Since \(x_0=2y_0+3,\) this gives \(x_0=5.\)

4. Next, we evaluate \(f(x,y)=x^2+4y^2−2x+8y\) at the point \((5,1)\), \[f(5,1)=5^2+4(1)^2−2(5)+8(1)=27. \nonumber \]To ensure this corresponds to a minimum value on the constraint function, let’s try some other points on the constraint from either side of the point \((5,1)\), such as the intercepts of \(g(x,y)=0\), Which are \((7,0)\) and \((0,3.5)\).

We get \(f(7,0)=35 \gt 27\) and \(f(0,3.5)=77 \gt 27\).

So it appears that \(f\) has a relative minimum of \(27\) at \((5,1)\), subject to the given constraint.

Exercise \(\PageIndex{1}\)

Use the method of Lagrange multipliers to find the maximum value of

\[f(x,y)=9x^2+36xy−4y^2−18x−8y \nonumber \]

subject to the constraint \(3x+4y=32.\)

Hint

Use the problem-solving strategy for the method of Lagrange multipliers.

Answer

Subject to the given constraint, \(f\) has a maximum value of \(976\) at the point \((8,2)\).

Let’s now return to the problem posed at the beginning of the section.

Example \(\PageIndex{2}\): Golf Balls and Lagrange Multipliers

The golf ball manufacturer, Pro-T, has developed a profit model that depends on the number \(x\) of golf balls sold per month (measured in thousands), and the number of hours per month of advertising y, according to the function

\[z=f(x,y)=48x+96y−x^2−2xy−9y^2, \nonumber \]

where \(z\) is measured in thousands of dollars. The budgetary constraint function relating the cost of the production of thousands golf balls and advertising units is given by \(20x+4y=216.\) Find the values of \(x\) and \(y\) that maximize profit, and find the maximum profit.

Solution:

Again, we follow the problem-solving strategy:

1. The objective function is \(f(x,y)=48x+96y−x^2−2xy−9y^2.\) To determine the constraint function, we first subtract \(216\) from both sides of the constraint, then divide both sides by \(4\), which gives \(5x+y−54=0.\) The constraint function is equal to the left-hand side, so \(g(x,y)=5x+y−54.\) The problem asks us to solve for the maximum value of \(f\), subject to this constraint.
2. So, we calculate the gradients of both \(f\) and \(g\): \[\begin{align*} \vecs ∇f(x,y) &=(48−2x−2y)\hat{\mathbf i}+(96−2x−18y)\hat{\mathbf j}\\[4pt]\vecs ∇g(x,y) &=5\hat{\mathbf i}+\hat{\mathbf j}. \end{align*}\] The equation \(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\) becomes \[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ(5\hat{\mathbf i}+\hat{\mathbf j}),\nonumber \] which can be rewritten as \[(48−2x_0−2y_0)\hat{\mathbf i}+(96−2x_0−18y_0)\hat{\mathbf j}=λ5\hat{\mathbf i}+λ\hat{\mathbf j}.\nonumber \] We then set the coefficients of \(\hat{\mathbf i}\) and \(\hat{\mathbf j}\) equal to each other: \[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ. \end{align*}\] The equation \(g(x_0,y_0)=0\) becomes \(5x_0+y_0−54=0\). Therefore, the system of equations that needs to be solved is \[\begin{align*} 48−2x_0−2y_0 =5λ \\[4pt] 96−2x_0−18y_0 =λ \\[4pt]5x_0+y_0−54 =0. \end{align*}\]
3. We use the left-hand side of the second equation to replace \(λ\) in the first equation: \[\begin{align*} 48−2x_0−2y_0 &=5(96−2x_0−18y_0) \\[4pt]48−2x_0−2y_0 &=480−10x_0−90y_0 \\[4pt] 8x_0 &=432−88y_0 \\[4pt] x_0 &=54−11y_0. \end{align*}\] Then we substitute this into the third equation: \[\begin{align*} 5(54−11y_0)+y_0−54 &=0\\[4pt] 270−55y_0+y_0-54 &=0\\[4pt]216−54y_0 &=0 \\[4pt]y_0 &=4. \end{align*}\] Since \(x_0=54−11y_0,\) this gives \(x_0=10.\)
4. We then substitute \((10,4)\) into \(f(x,y)=48x+96y−x^2−2xy−9y^2,\) which gives \[\begin{align*} f(10,4) &=48(10)+96(4)−(10)^2−2(10)(4)−9(4)^2 \\[4pt] &=480+384−100−80−144 \\[4pt] &=540.\end{align*}\] Therefore the maximum profit that can be attained, subject to budgetary constraints, is \($540,000\) with a production level of \(10,000\) golf balls and \(4\) hours of advertising bought per month. Let’s check to make sure this truly is a maximum. The endpoints of the line that defines the constraint are \((10.8,0)\) and \((0,54)\) Let’s evaluate \(f\) at both of these points: \[\begin{align*} f(10.8,0) &=48(10.8)+96(0)−10.8^2−2(10.8)(0)−9(0^2) \\[4pt] &=401.76 \\[4pt] f(0,54) &=48(0)+96(54)−0^2−2(0)(54)−9(54^2) \\[4pt] &=−21,060. \end{align*}\] The second value represents a loss, since no golf balls are produced. Neither of these values exceed \(540\), so it seems that our extremum is a maximum value of \(f\), subject to the given constraint.

Exercise \(\PageIndex{2}\): Optimizing the Cobb-Douglas function

A company has determined that its production level is given by the Cobb-Douglas function \(f(x,y)=2.5x^{0.45}y^{0.55}\) where \(x\) represents the total number of labor hours in \(1\) year and \(y\) represents the total capital input for the company. Suppose \(1\) unit of labor costs \($40\) and \(1\) unit of capital costs \($50\). Use the method of Lagrange multipliers to find the maximum value of \(f(x,y)=2.5x^{0.45}y^{0.55}\) subject to a budgetary constraint of \($500,000\) per year.

Hint

Use the problem-solving strategy for the method of Lagrange multipliers.

Answer

Subject to the given constraint, a maximum production level of \(13890\) occurs with \(5625\) labor hours and \($5500\) of total capital input.

In the case of an objective function with three variables and a single constraint function, it is possible to use the method of Lagrange multipliers to solve an optimization problem as well. An example of an objective function with three variables could be the Cobb-Douglas function in Exercise \(\PageIndex{2}\): \(f(x,y,z)=x^{0.2}y^{0.4}z^{0.4},\) where \(x\) represents the cost of labor, \(y\) represents capital input, and \(z\) represents the cost of advertising. The method is the same as for the method with a function of two variables; the equations to be solved are

\[\begin{align*} \vecs ∇f(x,y,z) &=λ\vecs ∇g(x,y,z) \\[4pt] g(x,y,z) &=0. \end{align*}\]

Example \(\PageIndex{3}\): Lagrange Multipliers with a Three-Variable objective function

Maximize the function \(f(x,y,z)=x^2+y^2+z^2\) subject to the constraint \(x+y+z=1.\)

Solution

1. The objective function is \(f(x,y,z)=x^2+y^2+z^2.\) To determine the constraint function, we subtract \(1\) from each side of the constraint: \(x+y+z−1=0\) which gives the constraint function as \(g(x,y,z)=x+y+z−1.\)

2. Next, we calculate \(\vecs ∇f(x,y,z)\) and \(\vecs ∇g(x,y,z):\) \[\begin{align*} \vecs ∇f(x,y,z) &=⟨2x,2y,2z⟩ \\[4pt] \vecs ∇g(x,y,z) &=⟨1,1,1⟩. \end{align*}\] This leads to the equations \[\begin{align*} ⟨2x_0,2y_0,2z_0⟩ &=λ⟨1,1,1⟩ \\[4pt] x_0+y_0+z_0−1 &=0 \end{align*}\] which can be rewritten in the following form: \[\begin{align*} 2x_0 &=λ\\[4pt] 2y_0 &=λ \\[4pt] 2z_0 &=λ \\[4pt] x_0+y_0+z_0−1 &=0. \end{align*}\]

3. Since each of the first three equations has \(λ\) on the right-hand side, we know that \(2x_0=2y_0=2z_0\) and all three variables are equal to each other. Substituting \(y_0=x_0\) and \(z_0=x_0\) into the last equation yields \(3x_0−1=0,\) so \(x_0=\frac{1}{3}\) and \(y_0=\frac{1}{3}\) and \(z_0=\frac{1}{3}\) which corresponds to a critical point on the constraint curve.

4. Then, we evaluate \(f\) at the point \(\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)\): \[f\left(\frac{1}{3},\frac{1}{3},\frac{1}{3}\right)=\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2+\left(\frac{1}{3}\right)^2=\dfrac{3}{9}=\dfrac{1}{3} \nonumber \] Therefore, a possible extremum of the function is \(\frac{1}{3}\). To verify it is a minimum, choose other points that satisfy the constraint from either side of the point we obtained above and calculate \(f\) at those points. For example, \[\begin{align*} f(1,0,0) &=1^2+0^2+0^2=1 \\[4pt] f(0,−2,3) &=0^2+(−2)^2+3^2=13. \end{align*}\] Both of these values are greater than \(\frac{1}{3}\), leading us to believe the extremum is a minimum, subject to the given constraint.

Exercise \(\PageIndex{3}\)

Use the method of Lagrange multipliers to find the minimum value of the function

\[f(x,y,z)=x+y+z \nonumber \]

subject to the constraint \(x^2+y^2+z^2=1.\)

Hint

Use the problem-solving strategy for the method of Lagrange multipliers with an objective function of three variables.

Answer

Evaluating \(f\) at both points we obtained, gives us, \[\begin{align*} f\left(\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3}\right) =\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}+\dfrac{\sqrt{3}}{3}=\sqrt{3} \\ f\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right) =−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}−\dfrac{\sqrt{3}}{3}=−\sqrt{3}\end{align*}\] Since the constraint is continuous, we compare these values and conclude that \(f\) has a relative minimum of \(−\sqrt{3}\) at the point \(\left(−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3},−\dfrac{\sqrt{3}}{3}\right)\), subject to the given constraint.

Problems with Two Constraints

The method of Lagrange multipliers can be applied to problems with more than one constraint. In this case the objective function, \(w\) is a function of three variables:

\[w=f(x,y,z) \nonumber \]

and it is subject to two constraints:

\[g(x,y,z)=0 \; \text{and} \; h(x,y,z)=0. \nonumber \]

There are two Lagrange multipliers, \(λ_1\) and \(λ_2\), and the system of equations becomes

\[\begin{align*} \vecs ∇f(x_0,y_0,z_0) &=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0) \\[4pt] g(x_0,y_0,z_0) &=0\\[4pt] h(x_0,y_0,z_0) &=0 \end{align*}\]

Example \(\PageIndex{4}\): Lagrange Multipliers with Two Constraints

Find the maximum and minimum values of the function

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

subject to the constraints \(z^2=x^2+y^2\) and \(x+y−z+1=0.\)

Solution

Let’s follow the problem-solving strategy:

1. The objective function is \(f(x,y,z)=x^2+y^2+z^2.\) To determine the constraint functions, we first subtract \(z^2\) from both sides of the first constraint, which gives \(x^2+y^2−z^2=0\), so \(g(x,y,z)=x^2+y^2−z^2\). The second constraint function is \(h(x,y,z)=x+y−z+1.\)
2. We then calculate the gradients of \(f,g,\) and \(h\): \[\begin{align*} \vecs ∇f(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}+2z\hat{\mathbf k} \\[4pt] \vecs ∇g(x,y,z) &=2x\hat{\mathbf i}+2y\hat{\mathbf j}−2z\hat{\mathbf k} \\[4pt] \vecs ∇h(x,y,z) &=\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}. \end{align*}\] The equation \(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\) becomes \[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=λ_1(2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}−2z_0\hat{\mathbf k})+λ_2(\hat{\mathbf i}+\hat{\mathbf j}−\hat{\mathbf k}), \nonumber \] which can be rewritten as \[2x_0\hat{\mathbf i}+2y_0\hat{\mathbf j}+2z_0\hat{\mathbf k}=(2λ_1x_0+λ_2)\hat{\mathbf i}+(2λ_1y_0+λ_2)\hat{\mathbf j}−(2λ_1z_0+λ_2)\hat{\mathbf k}. \nonumber \] Next, we set the coefficients of \(\hat{\mathbf i}\) and \(\hat{\mathbf j}\) equal to each other: \[\begin{align*}2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2. \end{align*}\] The two equations that arise from the constraints are \(z_0^2=x_0^2+y_0^2\) and \(x_0+y_0−z_0+1=0\). Combining these equations with the previous three equations gives \[\begin{align*} 2x_0 &=2λ_1x_0+λ_2 \\[4pt]2y_0 &=2λ_1y_0+λ_2 \\[4pt]2z_0 &=−2λ_1z_0−λ_2 \\[4pt]z_0^2 &=x_0^2+y_0^2 \\[4pt]x_0+y_0−z_0+1 &=0. \end{align*}\]
3. The first three equations contain the variable \(λ_2\). Solving the third equation for \(λ_2\) and replacing into the first and second equations reduces the number of equations to four: \[\begin{align*}2x_0 &=2λ_1x_0−2λ_1z_0−2z_0 \\[4pt] 2y_0 &=2λ_1y_0−2λ_1z_0−2z_0\\[4pt] z_0^2 &=x_0^2+y_0^2\\[4pt] x_0+y_0−z_0+1 &=0. \end{align*}\] Next, we solve the first and second equation for \(λ_1\). The first equation gives \(λ_1=\dfrac{x_0+z_0}{x_0−z_0}\), the second equation gives \(λ_1=\dfrac{y_0+z_0}{y_0−z_0}\). We set the right-hand side of each equation equal to each other and cross-multiply: \[\begin{align*} \dfrac{x_0+z_0}{x_0−z_0} &=\dfrac{y_0+z_0}{y_0−z_0} \\[4pt](x_0+z_0)(y_0−z_0) &=(x_0−z_0)(y_0+z_0) \\[4pt]x_0y_0−x_0z_0+y_0z_0−z_0^2 &=x_0y_0+x_0z_0−y_0z_0−z_0^2 \\[4pt]2y_0z_0−2x_0z_0 &=0 \\[4pt]2z_0(y_0−x_0) &=0. \end{align*}\] Therefore, either \(z_0=0\) or \(y_0=x_0\). If \(z_0=0\), then the first constraint becomes \(0=x_0^2+y_0^2\). The only real solution to this equation is \(x_0=0\) and \(y_0=0\), which gives the ordered triple \((0,0,0)\). This point does not satisfy the second constraint, so it is not a solution. Next, we consider \(y_0=x_0\), which reduces the number of equations to three: \[\begin{align*}y_0 &= x_0 \\[4pt] z_0^2 &= x_0^2 +y_0^2 \\[4pt] x_0 + y_0 -z_0+1 &=0. \end{align*} \nonumber \] We substitute the first equation into the second and third equations: \[\begin{align*} z_0^2 &= x_0^2 +x_0^2 \\[4pt] &= x_0+x_0-z_0+1 &=0. \end{align*} \nonumber \] Then, we solve the second equation for \(z_0\), which gives \(z_0=2x_0+1\). We then substitute this into the first equation, \[\begin{align*} z_0^2 &= 2x_0^2 \\[4pt] (2x_0^2 +1)^2 &= 2x_0^2 \\[4pt] 4x_0^2 + 4x_0 +1 &= 2x_0^2 \\[4pt] 2x_0^2 +4x_0 +1 &=0, \end{align*}\] and use the quadratic formula to solve for \(x_0\): \[ x_0 = \dfrac{-4 \pm \sqrt{4^2 -4(2)(1)} }{2(2)} = \dfrac{-4\pm \sqrt{8}}{4} = \dfrac{-4 \pm 2\sqrt{2}}{4} = -1 \pm \dfrac{\sqrt{2}}{2}. \nonumber \] Recall \(y_0=x_0\), so this solves for \(y_0\) as well. Then, \(z_0=2x_0+1\), so \[z_0 = 2x_0 +1 =2 \left( -1 \pm \dfrac{\sqrt{2}}{2} \right) +1 = -2 + 1 \pm \sqrt{2} = -1 \pm \sqrt{2} . \nonumber \] Therefore, there are two ordered triplet solutions: \[\left( -1 + \dfrac{\sqrt{2}}{2} , -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) \; \text{and} \; \left( -1 -\dfrac{\sqrt{2}}{2} , -1 -\dfrac{\sqrt{2}}{2} , -1 -\sqrt{2} \right). \nonumber \]
4. We substitute \(\left(−1+\dfrac{\sqrt{2}}{2},−1+\dfrac{\sqrt{2}}{2}, −1+\sqrt{2}\right) \) into \(f(x,y,z)=x^2+y^2+z^2\), which gives \[\begin{align*} f\left( -1 + \dfrac{\sqrt{2}}{2}, -1 + \dfrac{\sqrt{2}}{2} , -1 + \sqrt{2} \right) &= \left( -1+\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 + \dfrac{\sqrt{2}}{2} \right)^2 + (-1+\sqrt{2})^2 \\[4pt] &= \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + \left( 1-\sqrt{2}+\dfrac{1}{2} \right) + (1 -2\sqrt{2} +2) \\[4pt] &= 6-4\sqrt{2}. \end{align*}\] Then, we substitute \(\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2}\right)\) into \(f(x,y,z)=x^2+y^2+z^2\), which gives \[\begin{align*} f\left(−1−\dfrac{\sqrt{2}}{2}, -1+\dfrac{\sqrt{2}}{2}, -1+\sqrt{2} \right) &= \left( -1-\dfrac{\sqrt{2}}{2} \right)^2 + \left( -1 - \dfrac{\sqrt{2}}{2} \right)^2 + (-1-\sqrt{2})^2 \\[4pt] &= \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + \left( 1+\sqrt{2}+\dfrac{1}{2} \right) + (1 +2\sqrt{2} +2) \\[4pt] &= 6+4\sqrt{2}. \end{align*}\] \(6+4\sqrt{2}\) is the maximum value and \(6−4\sqrt{2}\) is the minimum value of \(f(x,y,z)\), subject to the given constraints.

Exercise \(\PageIndex{4}\)

Use the method of Lagrange multipliers to find the minimum value of the function

\[f(x,y,z)=x^2+y^2+z^2 \nonumber \]

subject to the constraints \(2x+y+2z=9\) and \(5x+5y+7z=29.\)

Hint

Use the problem-solving strategy for the method of Lagrange multipliers with two constraints.

Answer

\(f(2,1,2)=9\) is a minimum value of \(f\), subject to the given constraints.

Key Concepts

• An objective function combined with one or more constraints is an example of an optimization problem.
• To solve optimization problems, we apply the method of Lagrange multipliers using a four-step problem-solving strategy.

Key Equations

• Method of Lagrange multipliers, one constraint

\(\vecs ∇f(x_0,y_0)=λ\vecs ∇g(x_0,y_0)\)

\(g(x_0,y_0)=0\)

• Method of Lagrange multipliers, two constraints

\(\vecs ∇f(x_0,y_0,z_0)=λ_1\vecs ∇g(x_0,y_0,z_0)+λ_2\vecs ∇h(x_0,y_0,z_0)\)

\(g(x_0,y_0,z_0)=0\)

\(h(x_0,y_0,z_0)=0\)

Glossary

constraint

an inequality or equation involving one or more variables that is used in an optimization problem; the constraint enforces a limit on the possible solutions for the problem

Lagrange multiplier

the constant (or constants) used in the method of Lagrange multipliers; in the case of one constant, it is represented by the variable \(λ\)

method of Lagrange multipliers

a method of solving an optimization problem subject to one or more constraints

objective function

the function that is to be maximized or minimized in an optimization problem

optimization problem

calculation of a maximum or minimum value of a function of several variables, often using Lagrange multipliers