6.3: Trigonometric Integrals

Functions involving trigonometric functions are useful as they are good at describing periodic behavior. This section describes several techniques for finding antiderivatives of certain combinations of trigonometric functions.

Integrals of the form $\int \sin^m x\cos^n x\ dx$

In learning the technique of Substitution, we saw the integral $\int \sin x\cos x\ dx$ in Example 6.1.4. The integration was not difficult, and one could easily evaluate the indefinite integral by letting $u=\sin x$ or by letting $u = \cos x$. This integral is easy since the power of both sine and cosine is 1.

We generalize this integral and consider integrals of the form $\int \sin^mx\cos^nx\ dx$, where $m,n$ are nonnegative integers. Our strategy for evaluating these integrals is to use the identity $\cos^2x+\sin^2x=1$ to convert high powers of one trigonometric function into the other, leaving a single sine or cosine term in the integrand. We summarize the general technique in the following Key Idea.

Key Idea 11: Integrals Involving Powers of Sine and Cosine

Consider $\int \sin^mx\cos^nx\ dx$, where $m,n$ are nonnegative integers.

1. If $m$ is odd, then $m=2k+1$ for some integer $k$. Rewrite $$\sin^mx = \sin^{2k+1}x = \sin^{2k}x\sin x = (\sin^2x)^k\sin x = (1-\cos^2x)^k\sin x.$$ Then $$\int \sin^mx\cos^nx\ dx = \int (1-\cos^2x)^k\sin x\cos^nx\ dx = -\int (1-u^2)^ku^n\ du,$$ where $u = \cos x$ and $du = -\sin x\ dx$.
2. If $n$ is odd, then using substitutions similar to that outlined above we have $$\int \sin^mx\cos^nx\ dx = \int u^m(1-u^2)^k\ du,$$ where $u = \sin x$ and $du = \cos x\ dx$.
3. If both $m$ and $n$ are even, use the power--reducing identities $$\cos^2x = \frac{1+\cos (2x)}{2} \quad \text{and}\quad \sin^2x = \frac{1-\cos(2x)}2$$ to reduce the degree of the integrand. Expand the result and apply the principles of this Key Idea again.

We practice applying Key Idea 11 in the next examples.

Example $\PageIndex{1}$: Integrating powers of sine and cosine

Evaluate $\int\sin^5x\cos^8x\ dx$.

Solution

The power of the sine term is odd, so we rewrite $\sin^5x$ as

$$\sin^5x = \sin^4x\sin x = (\sin^2x)^2\sin x = (1-\cos^2x)^2\sin x. \nonumber$$

Our integral is now $\int (1-\cos^2x)^2\cos^8x\sin x\ dx$. Let $u = \cos x$, hence $du = -\sin x\ dx$. Making the substitution and expanding the integrand gives

$$\int (1-\cos^2)^2\cos^8x\sin x\ dx = -\int (1-u^2)^2u^8\ du = -\int \big(1-2u^2+u^4\big)u^8\ du = -\int \big(u^8-2u^{10}+u^{12}\big)\ du. \nonumber$$

This final integral is not difficult to evaluate, giving

$$\begin{align*} -\int \big(u^8-2u^{10}+u^{12}\big)\ du &= -\frac19u^9 + \frac2{11}u^{11} - \frac1{13}u^{13} + C \\[4pt] &=-\frac19\cos^9 x + \frac2{11}\cos^{11} x - \frac1{13}\cos^{13} x + C.\end{align*}$$

Example $\PageIndex{2}$: Integrating powers of sine and cosine

Evaluate $\int\sin^5x\cos^9x\ dx$.

Solution

The powers of both the sine and cosine terms are odd, therefore we can apply the techniques of Key Idea 11 to either power. We choose to work with the power of the cosine term since the previous example used the sine term's power.

We rewrite $\cos^9x$ as

$$\begin{align*} \cos^9 x &= \cos^8x\cos x \\[4pt] &= (\cos^2x)^4\cos x \\[4pt] &= (1-\sin^2x)^4\cos x \\[4pt] &= (1-4\sin^2x+6\sin^4x-4\sin^6x+\sin^8x)\cos x.\end{align*}$$

We rewrite the integral as

$$\int\sin^5x\cos^9x\ dx = \int\sin^5x\big(1-4\sin^2x+6\sin^4x-4\sin^6x+\sin^8x\big)\cos x\ dx. \nonumber$$

Now substitute and integrate, using $u = \sin x$ and $du = \cos x\ dx$.

$$\begin{align*} \int u^5(1-4u^2+6u^4-4u^6+u^8)\ du &= \int\big(u^5-4u^7+6u^9-4u^{11}+u^{13}\big)\ du \\[4pt]&= \frac16u^6-\frac12u^8+\frac35u^{10}-\frac13u^{12}+\frac{1}{14}u^{14}+C\\[4pt] &= \frac16\sin^6 x-\frac12\sin^8 x+\frac35\sin^{10} x+\ldots\\[4pt]&\phantom{=}-\frac13\sin^{12} x+\frac{1}{14}\sin^{14} x+C.\end{align*}$$

Technology Note: The work we are doing here can be a bit tedious, but the skills developed (problem solving, algebraic manipulation, etc.) are important. Nowadays problems of this sort are often solved using a computer algebra system. The powerful program Mathematica integrates $\int \sin^5x\cos^9x\ dx$ as

$$f(x)=-\frac{45 \cos (2 x)}{16384}-\frac{5 \cos (4 x)}{8192}+\frac{19 \cos (6x)}{49152}+\frac{\cos (8x)}{4096}-\frac{\cos (10 x)}{81920}-\frac{\cos (12 x)}{24576}-\frac{\cos (14 x)}{114688},$$

which clearly has a different form than our answer in Example $\PageIndex{2}$, which is

$$g(x)=\frac16\sin^6 x-\frac12\sin^8 x+\frac35\sin^{10} x-\frac13\sin^{12} x+\frac{1}{14}\sin^{14} x.$$

Figure $\PageIndex{1}$ shows a graph of $f$ and $g$; they are clearly not equal, but they differ only by a constant. That is $g(x) = f(x) + C$ for some constant $C$. So we have two different antiderivatives of the same function, meaning both answers are correct.

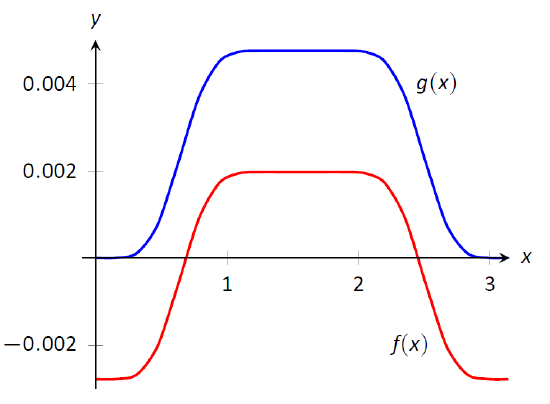
Figure $\PageIndex{1}$: A plot of $f(x)$ and $g(x)$ from Example $\PageIndex{2}$ and the Technology Note.

Example $\PageIndex{3}$: Integrating powers of sine and cosine

Evaluate $\int\cos^4x\sin^2x\ dx$.

Solution

The powers of sine and cosine are both even, so we employ the power--reducing formulas and algebra as follows.

$$\begin{align*}\int \cos^4x\sin^2x\ dx &= \int\left(\frac{1+\cos(2x)}{2}\right)^2\left(\frac{1-\cos(2x)}2\right)\ dx \\[4pt] &= \int\frac{1+2\cos(2x)+\cos^2(2x)}4\cdot\frac{1-\cos(2x)}2\ dx\\[4pt] &= \int \frac18\big(1+\cos(2x)-\cos^2(2x)-\cos^3(2x)\big)\ dx\end{align*}$$

The $\cos(2x)$ term is easy to integrate, especially with Key Idea 10. The $\cos^2(2x)$ term is another trigonometric integral with an even power, requiring the power--reducing formula again. The $\cos^3(2x)$ term is a cosine function with an odd power, requiring a substitution as done before. We integrate each in turn below.

$$\int\cos(2x)\ dx = \frac12\sin(2x)+C.\nonumber$$

$$\int\cos^2(2x)\ dx = \int \frac{1+\cos(4x)}2\ dx = \frac12\big(x+\frac14\sin(4x)\big)+C. \nonumber$$

Finally, we rewrite $\cos^3(2x)$ as

$$\cos^3(2x) = \cos^2(2x)\cos(2x) = \big(1-\sin^2(2x)\big)\cos(2x).$$

Letting $u=\sin(2x)$, we have $du = 2\cos(2x)\ dx$, hence

$$\begin{align*} \int \cos^3(2x)\ dx &= \int\big(1-\sin^2(2x)\big)\cos(2x)\ dx\\[4pt] &= \int \frac12(1-u^2)\ du\\[4pt] &= \frac12\Big(u-\frac13u^3\Big)+C\\[4pt] &= \frac12\Big(\sin(2x)-\frac13\sin^3(2x)\Big)+C\end{align*}$$

Putting all the pieces together, we have

$$\begin{align*}\int \cos^4x\sin^2x\ dx &=\int \frac18\big(1+\cos(2x)-\cos^2(2x)-\cos^3(2x)\big)\ dx \\[4pt] &= \frac18\Big[x+\frac12\sin(2x)-\frac12\big(x+\frac14\sin(4x)\big)-\frac12\Big(\sin(2x)-\frac13\sin^3(2x)\Big)\Big]+C \\[4pt] &=\frac18\Big[\frac12x-\frac18\sin(4x)+\frac16\sin^3(2x)\Big]+C\end{align*}$$

The process above was a bit long and tedious, but being able to work a problem such as this from start to finish is important.

Integrals of the form $\int\sin(mx)\sin(nx)\ dx,$ $\int \cos(mx)\cos(nx)\ dx$, and $\int \sin(mx)\cos(nx)\ dx$.

Functions that contain products of sines and cosines of differing periods are important in many applications including the analysis of sound waves. Integrals of the form

$$\int\sin(mx)\sin(nx)\ dx,\quad \int \cos(mx)\cos(nx)\ dx \quad \text{and}\quad\int \sin(mx)\cos(nx)\ dx$$

are best approached by first applying the Product to Sum Formulas found in the back cover of this text, namely

$$\begin{align*} \sin(mx)\sin(nx) &= \frac12\Big[\cos\big((m-n)x\big)-\cos\big((m+n)x\big)\Big] \\[4pt]\cos(mx)\cos(nx) &= \frac12\Big[\cos\big((m-n)x\big)+\cos\big((m+n)x\big)\Big] \\[4pt]\sin(mx)\cos(nx) &= \frac12\Big[\sin\big((m-n)x\big)+\sin\big((m+n)x\big)\Big]\end{align*}$$

Example $\PageIndex{4}$: Integrating products of $\sin(mx)$ and $\cos(nx)$

Evaluate $\int\sin(5x)\cos(2x)\ dx$.

Solution

The application of the formula and subsequent integration are straightforward:

$$\begin{align*}\int\sin(5x)\cos(2x)\ dx &= \int \frac12\Big[\sin(3x)+\sin(7x)\Big]\ dx \\[4pt] &= -\frac16\cos(3x) - \frac1{14}\cos(7x) + C\end{align*}$$

Integrals of the form $\int\tan^mx\sec^nx\ dx$.

When evaluating integrals of the form $\int \sin^mx\cos^nx\ dx$, the Pythagorean Theorem allowed us to convert even powers of sine into even powers of cosine, and vise--versa. If, for instance, the power of sine was odd, we pulled out one $\sin x$ and converted the remaining even power of $\sin x$ into a function using powers of $\cos x$, leading to an easy substitution.

The same basic strategy applies to integrals of the form $\int \tan^mx\sec^n x\ dx$, albeit a bit more nuanced. The following three facts will prove useful:

1. $\frac{d}{dx}(\tan x) = \sec^2x$,
2. $\frac{d}{dx}(\sec x) = \sec x\tan x$, and
3. $1+\tan^2x = \sec^2x$ (the Pythagorean Theorem).

If the integrand can be manipulated to separate a $\sec^2x$ term with the remaining secant power even, or if a $\sec x\tan x$ term can be separated with the remaining $\tan x$ power even, the Pythagorean Theorem can be employed, leading to a simple substitution. This strategy is outlined in the following Key Idea.

Key Idea 12: Integrals Involving Powers of Tangent and Secant

Consider $\int\tan^mx\sec^nx\ dx$, where $m,n$ are nonnegative integers.

1. If $n$ is even, then $n=2k$ for some integer $k$. Rewrite $\sec^nx$ as $$\sec^nx = \sec^{2k}x = \sec^{2k-2}x\sec^2x = (1+\tan^2x)^{k-1}\sec^2x.$$ Then $$\int\tan^mx\sec^nx\ dx=\int\tan^mx(1+\tan^2x)^{k-1}\sec^2x\ dx = \int u^m(1+u^2)^{k-1}\ du,$$ where $u = \tan x$ and $du = \sec^2x\ dx$.
2. If $m$ is odd, then $m=2k+1$ for some integer $k$. Rewrite $\tan^mx\sec^nx$ as $$\tan^mx\sec^nx = \tan^{2k+1}x\sec^nx = \tan^{2k}x\sec^{n-1}x\sec x\tan x = (\sec^2x-1)^k\sec^{n-1}x\sec x\tan x.$$ Then $$\int\tan^mx\sec^nx\ dx=\int(\sec^2x-1)^k\sec^{n-1}x\sec x\tan x\ dx = \int(u^2-1)^ku^{n-1}\ du,$$ where $u = \sec x$ and $du = \sec x\tan x\ dx$.
3. If $n$ is odd and $m$ is even, then $m=2k$ for some integer $k$. Convert $\tan^mx$ to $(\sec^2x-1)^k$. Expand the new integrand and use Integration By Parts, with $dv = \sec^2x\ dx$.
4. If $m$ is even and $n=0$, rewrite $\tan^mx$ as $$\tan^mx = \tan^{m-2}x\tan^2x = \tan^{m-2}x(\sec^2x-1) = \tan^{m-2}\sec^2x-\tan^{m-2}x.$$ So $$\int\tan^mx\ dx = \underbrace{\int\tan^{m-2}\sec^2x\ dx}_{\text{\small apply rule \#1}}\quad - \underbrace{\int\tan^{m-2}x\ dx}_{\text{\small apply rule \#4 again}}.$$

The techniques described in items 1 and 2 of Key Idea 12 are relatively straightforward, but the techniques in items 3 and 4 can be rather tedious. A few examples will help with these methods.

Example $\PageIndex{5}$: Integrating powers of tangent and secant

Evaluate $\int \tan^2x\sec^6x\ dx$.

Solution

Since the power of secant is even, we use rule #1 from Key Idea 12 and pull out a $\sec^2x$ in the integrand. We convert the remaining powers of secant into powers of tangent.

$$\begin{align*}\int \tan^2x\sec^6x\ dx &= \int\tan^2x\sec^4x\sec^2x\ dx \\[4pt] &= \int \tan^2x\big(1+\tan^2x\big)^2\sec^2x\ dx \end{align*}$$

Now substitute, with $u=\tan x$, with $du = \sec^2x\ dx$.

$$=\int u^2\big(1+u^2\big)^2\ du \nonumber$$

We leave the integration and subsequent substitution to the reader. The final answer is

$$=\frac13\tan^3x+\frac25\tan^5x+\frac17\tan^7x+C. \nonumber$$

Example $\PageIndex{6}$: Integrating powers of tangent and secant

Evaluate $\int \sec^3x\ dx$.

Solution

We apply rule #3 from Key Idea 12 as the power of secant is odd and the power of tangent is even (0 is an even number). We use Integration by Parts; the rule suggests letting $dv = \sec^2x\ dx$, meaning that $u = \sec x$.

$$\begin{align*}u&= \sec x & v&=\text{?}\\[4pt]du&= \text{?} & dv&=\sec^2 x\ dx\end{align*}$$

Figure $\PageIndex{2}$: Setting up Integration by Parts.

Employing Integration by Parts, we have

$$\begin{align*}\int \sec^3x\ dx &= \int \underbrace{\sec x}_u\cdot\underbrace{\sec^2 x\ dx}_{dv}\\[4pt] &= \sec x\tan x - \int \sec x\tan^2x\ dx. \end{align*}$$

This new integral also requires applying rule \#3 of Key Idea:

$$\begin{align*} &= \sec x\tan x - \int \sec x \big(\sec^2 x-1\big)\ dx\\[4pt] &= \sec x\tan x - \int \sec^3x\ dx + \int \sec x\ dx \\[4pt] &= \sec x\tan x -\int \sec^3x\ dx + \ln|\sec x+\tan x| \\[4pt] \end{align*}$$

In previous applications of Integration by Parts, we have seen where the original integral has reappeared in our work. We resolve this by adding $\int \sec^3x\ dx$ to both sides, giving:

$$\begin{align*} 2\int \sec^3x\ dx &= \sec x\tan x + \ln|\sec x+\tan x| \\[4pt]\int \sec^3x\ dx &= \frac12\Big(\sec x\tan x + \ln|\sec x+\tan x|\Big)+C\end{align*}$$

We give one more example.

Example $\PageIndex{7}$: Integrating powers of tangent and secant

Evaluate $\int\tan^6x\ dx$.

Solution

We employ rule #4 of Key Idea 12.

$$\begin{align*} \int \tan^6x\ dx &= \int \tan^4x\tan^2x\ dx \\[4pt] &= \int\tan^4x\big(\sec^2x-1\big)\ dx\\[4pt] &= \int\tan^4x\sec^2x\ dx - \int\tan^4x\ dx \end{align*}$$

Integrate the first integral with substitution, $u=\tan x$; integrate the second by employing rule #4 again.

$$\begin{align*} &= \frac15\tan^5x-\int\tan^2x\tan^2x\ dx\\[4pt] &= \frac15\tan^5x-\int\tan^2x\big(\sec^2x-1\big)\ dx \\[4pt]&= \frac15\tan^5x -\int\tan^2x\sec^2x\ dx + \int\tan^2x\ dx\\[4pt] \end{align*}$$

Again, use substitution for the first integral and rule \#4 for the second.

$$\begin{align*} &= \frac15\tan^5x-\frac13\tan^3x+\int\big(\sec^2x-1\big)\ dx \\[4pt] &= \frac15\tan^5x-\frac13\tan^3x+\tan x - x+C. \end{align*}$$

These latter examples were admittedly long, with repeated applications of the same rule. Try to not be overwhelmed by the length of the problem, but rather admire how robust this solution method is. A trigonometric function of a high power can be systematically reduced to trigonometric functions of lower powers until all antiderivatives can be computed.

The next section introduces an integration technique known as Trigonometric Substitution, a clever combination of Substitution and the Pythagorean Theorem.

Contributors and Attributions

• Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/

• Integrated by Justin Marshall.