5.1: The Equation of a Tangent Line
- Page ID
- 121106
- Given a simple function \(y=f(x)\) and a point \(x\), be able to find the equation of the tangent line to the graph at that point.
- Graph both a function and its tangent line using a spreadsheet or your favorite software.
In the following examples, the equation of the tangent line is easily found.
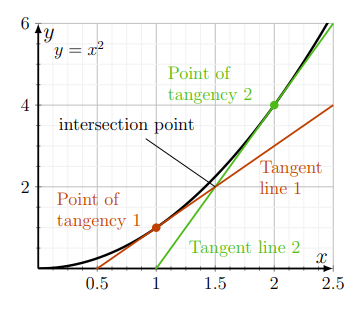
Find the equations of the tangent lines to the parabola \(y=f(x)=x^{2}\) at the points:
- \(x=1\) and \(x=2\) ("Line 1" and "Line 2 ").
- Determine whether these tangent lines intersect, and if so, where.
Solution
a) This means \(m_{1}=f^{\prime}(1)=2 \cdot 1=2\) (for Line 1) and \(m_{2}=f^{\prime}(2)=2 \cdot 2=4\) (for Line 2). The points of tangency are on the curve \(\left(x, x^{2}\right)\). Thus these are \((1,1)\) for Line 1 and \((2,4)\) for Line 2 .
With the slope and a point for each line, we find that
Line 1: \(\frac{y-1}{x-1}=m_{1}=2, \quad \Rightarrow \quad y=1+2(x-1) \quad \Rightarrow \quad y=2 x-1\),
Line 2: \(\frac{y-4}{x-2}=m_{2}=4 \quad \Rightarrow \quad y=4+4(x-2) \quad \Rightarrow \quad y=4 x-4\).
b) Two lines intersect if their \(y\) values (and \(x\) values) are the same. Equating \(y\) values and solving for \(x\), we get
\[2 x-1=4 x-4 \quad \Rightarrow \quad-2 x=-3 \quad \Rightarrow \quad x=\frac{3}{2} . \nonumber \]
Hence, the two tangent lines intersect at \(x=3 / 2\) as shown in Fig 5.1.The next example illustrates how a tangent line can be used to approximate the zero of a function. This idea is developed into a useful approximation method called Newton’s method in Section 5.4.
What are the slope and \(y\)-intercept of the generic tangent line (given in Equation (5.1))?
Solution
The slopes of a tangent line is a derivative, which in this case is \(f^{\prime}(x)=2 x\).
- Draw the graph of the function \(y=f(x)=x^{3}-x\) together with its tangent line at the point \(x=1.5\).
- Where does that tangent line intersect the \(x\)-axis?
- Compare that point of intersection with a zero of the function.
Solution
a) The function is \(f(x)=x^{3}-x\), its derivative is \(f^{\prime}(x)=3 x^{2}-1\), and the point of interest is \((x, f(x))=(1.5,1.875)\). A tangent line at \(x=1.5\) has slope \(f^{\prime}(1.5)=3(1.5)^{2}-1=5.75\), so its equation is
\[\begin{aligned} \frac{y-1.875}{x-1.5}=5.75 & \Rightarrow & y & =1.875+5.75(x-1.5) \\ & \Rightarrow & y & =5.75 x-6.75 . \end{aligned} \nonumber \]
The function and this tangent line are shown in Figure 5.2.
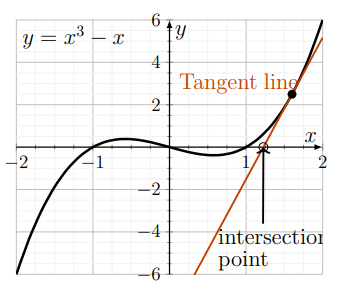
b) The tangent line intersects the \(x\)-axis when \(y=0\), which occurs at
\[0=5.75 x-6.75 \quad \Rightarrow \quad x=\frac{6.75}{5.75}=1.174 \nonumber \]
c) A true zero of the function is a value of \(x\) for which \(x^{3}-x=0\), and the one closest to the result in (b) is \(x=1\). Thus the point \((1.174,0)\) where the tangent line intersects the \(x\)-axis is close but not quite equal to \((1,0)\). (But Newton’s method will help us fix this gap.)
In many cases, directly solving for roots of functions (as in Example 5.2c) is not possible. In Section 5.4 we discuss how a repetition of this idea can be used to refine the approximation of a zero using Newton’s method.
Manipulate the slider to see the tangent line at various points on the graph of this function. Here \(D(x)\) represents the derivative, \(D(x)=d f / d x\), and \(x_{0}\) is the point of tangency. You can zoom in or out, change the range of the slider, or try a different function.
- Under what circumstance do two lines not intersect?
- Find the equation of the tangent line to \(y=f(x)=x^{3}-\rho x\) for \(\rho>0\) constant, at the point \(x=1\).
- Find where that tangent line intersects the \(x\)-axis.
Solution
This is the same type of calculation, but the constant, \(\rho\) - chosen to develop familiarity with alternative constant choices - makes the example slightly less straightforward.
a) The derivative of \(f(x)=x^{3}-\rho x\) is \(f^{\prime}(x)=3 x^{2}-\rho\) so at \(x=1\), the slope is \(m=f^{\prime}(1)=3-\rho\). The point of tangency is \((1, f(1))=(1,1-\rho)\). Then, the equation of the tangent line is
\[\begin{aligned} \frac{y-(1-\rho)}{x-1}=3-\rho . & \Rightarrow \quad y=(3-\rho)(x-1)+(1-\rho) \\ & \Rightarrow \quad y=(3-\rho) x-2 . \end{aligned} \nonumber \]
b) To find the point of intersection, set \(y=(3-\rho) x-2=0\) and solve for \(x\) to obtain \(x=2 /(3-\rho)\).
Find the equation of the tangent line to the function \(y=f(x)=\) \(\sqrt{x}\) at the point \(x=4\).
Solution
By Equation (3.5), the derivative of \(y=f(x)=\sqrt{x}\) is
\[f^{\prime}(x)=\frac{1}{(2 \sqrt{x})} \nonumber \]
At \(x=4\), the slope is \(f^{\prime}(4)=1 /(2 \sqrt{4})=1 / 4\) and the point of tangency is \((4, \sqrt{4})=(4,2)\). Given this point and the slope, we calculate that the tangent line is:
\[\frac{y-2}{x-4}=0.25 \Rightarrow y=2+0.25(x-4) . \nonumber \]
- How many zeros does the function depicted in Figure \(5.2\) have?
- Check that the tangent line goes through the desired point and has the slope we found. One way to do this is to pick a simple value for \(\rho\), e.g. \(\rho=1\) and do a quick check that the answer matches what we have found.
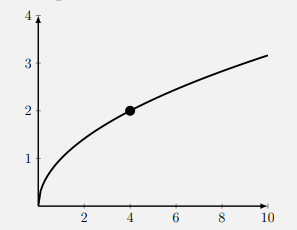
- The following graph depicts \(f(x)=\sqrt{x}\) on the interval \([0,10]\). Draw its tangent line at the point \(x=4\).
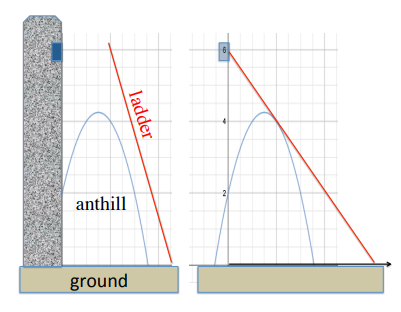
Featured Problem 5.1 (Shortest ladder): In Figure 5.3, what is the shortest ladder that you can use to reach the window at 6 meters height in the tower if there is an anthill in the way? Assume that the equation of the anthill is \(y=f(x)=-x^{2}+3 x+2\)