6.1: Overall Shape of the Graph of a Function

Learning Objectives

1. Identify that the sign of the first derivative corresponds to the increasing or decreasing trend of a function.
2. Recognize that the sign of the second derivative corresponds to the concavity (curvature) of a function.

Increasing and decreasing functions

Consider a function given by \(y=f(x)\). We first make the following observations:

1. If \(f^{\prime}(x)>0\) then \(f(x)\) is increasing.
2. If \(f^{\prime}(x)<0\) then \(f(x)\) is decreasing.

By convention, we read graphs from left to right, i.e. in the direction of the positive \(x\)-axis, so when we say "increasing" we mean that, as we move from left to right, the value of the function gets larger.

We can use the same ideas to relate the second derivative to the first derivative.

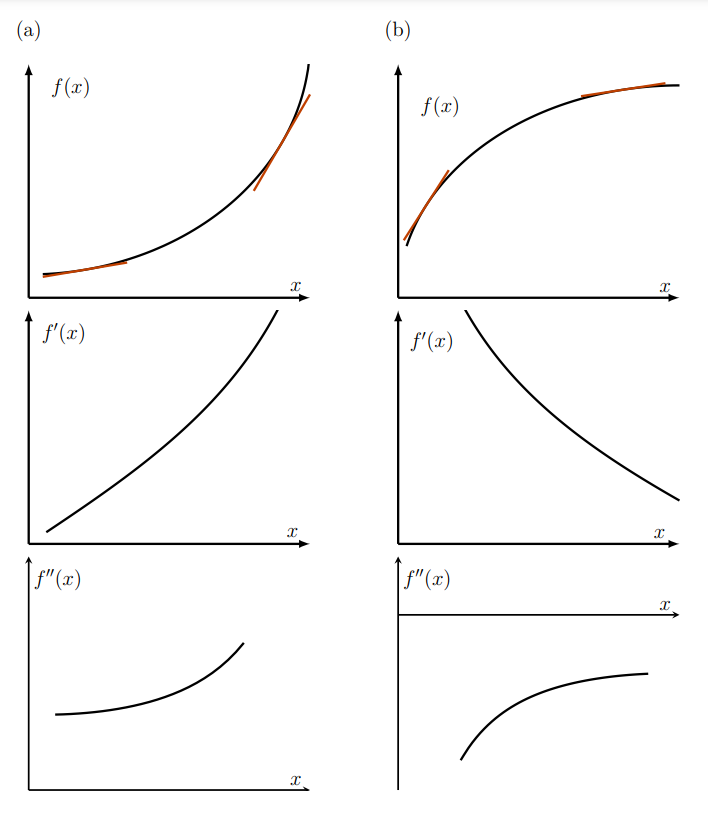
1. If \(f^{\prime \prime}(x)>0\) then \(f^{\prime}(x)\) is increasing. This means that the slope of the original function is getting steeper (more positive, from left to right). The function curves upwards: we say that it is concave up. See Figure 6.1(a).
2. If \(f^{\prime \prime}(x)<0\) then \(f^{\prime}(x)\) is decreasing. This means that the slope of the original function is getting shallower (more negative or less positive from left to right). The function curves downwards: we say that it is concave down. See Figure 6.1(b).

Figure 6.1: In (a) the function is concave up, and its derivative increases (in the positive direction). In (b), the function is concave down, and its derivative decreases.

Mastered Material Check

1. Draw the graphs of two different functions that are increasing on the interval \([0,1]\).
2. Without using the derivative, how do you identify when a function is decreasing?

Concavity and points of inflection

The second derivative of a function provides information about the curvature of the graph of the function, also called the concavity of the function.

• In Figure 6.1(a), \(f(x)\) is concave up, so its second derivative is positive.
• In Figure 6.1(b), \(f(x)\) is concave down, so second derivative is negative.

See video summarizing the connection between the shape of the graph of \(y = f(x)\), and the derivatives of the function, \(f^{\prime}(x)\), \(f^{\prime \prime}(x)\) of the function.

Definition 6.1

A point of inflection of a function \(f(x)\) is a point \(x\) at which the concavity of the function changes (Figure 6.2). We can deduce from the definition and previous remarks that at a point of inflection the second derivative changes sign. This is illustrated in Figure 6.2. Note: It is not enough to show that \(f^{\prime \prime}(x)=0\) to conclude that \(x\) is an inflection point. We summarize the one-way nature of this relationship in the box and discuss it further in Example 6.1.

Figure 6.2: An inflection point is a place where the concavity of a function changes.

Inflection points

1. If the function \(y=f(x)\) has a point of inflection at \(x_{0}\) then \(f^{\prime \prime}\left(x_{0}\right)=0\).
2. If the function \(y=f(x)\) satisfies \(f^{\prime \prime}\left(x_{0}\right)=0\), we cannot conclude that it has a point of inflection at \(x_{0}\). We must actually check that \(f^{\prime \prime}(x)\) changes sign at \(x_{0}\).

Example 6.1

Consider the the functions (a) \(f_{1}(x)=x^{3}\) and \((b) f_{2}(x)=x^{4}\). Show that for both functions, the second derivative is zero at the origin \(\left(f^{\prime \prime}(0)=0\right)\) but that only one of these functions actually has an inflection point at \(x=0\).

Solution

The functions are

(a) \(f_{1}(x)=x^{3}\)

(b) \(f_{2}(x)=x^{4}\).

The first derivatives are

(a) \(f_{1}^{\prime}(x)=3 x^{2}\)

(b) \(f_{2}^{\prime}(x)=4 x^{3}\).

The second derivatives are

(a) \(f_{1}^{\prime \prime}(x)=6 x\) (

b) \(f_{2}^{\prime \prime}(x)=12 x^{2}\).

Figure 6.3: The functions (a) \(f_{1}(x)=x^{3}\) and (b) \(f_{2}(x)=x^{4}\) both satisfy \(f^{\prime \prime}(0)=0\). However, only \(x^{3}\) has an inflection point at \(x=0\), whereas \(x^{4}\) has a local minimum at that point. This is not a contradiction, since \(f_{2}^{\prime \prime}(x)\) does not change sign at \(x=0\).

Thus, at \(x=0\) we have \(f_{1}^{\prime \prime}(0)=0, f_{2}^{\prime \prime}(0)=0\). However, \(x=0\) is NOT an inflection point of \(x^{4}\). In fact, it is a local minimum, as shown in Figure 6.3.

A summary of Example \(6.1\) reinforcing the fact that \(f^{\prime \prime}(x)=0\) is not enough to guarantee an inflection point! We have to check that \(f^{\prime \prime}(x)\) changes sign.

Mastered Material Check

3. Check that \(f(x)=x^{4}\) does not change sign at \(x=0\) by comparing the signs of \(f(-0.1)\) and \(f(0.1)\). Determining whether \(f^{\prime \prime}(x)\) changes sign

Determining whether \(f^{\prime \prime}(x)\) changes sign

We defined an inflection point as a point on the graph of a function where the second derivative changes sign. But how do we detect if this sign change occurs at a given point?

We first state the following result

Sign change in a product of factors

If an expression is a product of factors, e.g. \(g(x)=\left(x-a_{1}\right)^{n_{1}}\left(x-a_{2}\right)^{n_{2}} \ldots(x-\) \(\left.a_{m}\right)^{n_{m}}\), then

1. The expression can be zero only at the points \(x=a_{1}, a_{2}, \ldots, a_{m}\).
2. The expression changes sign only at points \(x=a_{i}\) for which \(n_{i}\) is an odd integer power.

How we check where \(f^{\prime \prime}(x)\) changes sign (to identify inflection points).

Example 6.2

Determine where \(g(x)=x^{2}(x+2)(x-3)^{4}\) changes sign.

Solution

The zeros of \(g(x)\) are \(x=0,-2,3\). At \(x=0\) and at \(x=3\) there is no sign change as the terms \(x^{2}\) and \((x-3)^{4}\) are always positive. The factor \((x+2)\) goes from negative through zero to positive when \(x\) goes from \(x<-2\) to \(x=-2\) to \(x>-2\). Hence, \(g(x)\) only changes sign at \(x=-2\).

Example 6.3

Where does the function \(f(x)=(2 / 5) x^{6}-x^{4}+x\) have inflection point(s)?

Solution

The derivatives of the function are

\[\begin{aligned} f^{\prime}(x) & =(12 / 5) x^{5}-4 x^{3}+1 \\ f^{\prime \prime}(x) & =12 x^{4}-14 x^{2}=12 x^{2}\left(x^{2}-1\right)=12 x^{2}(x+1)(x-1) \end{aligned} \nonumber \]

Here we have completely factored the second derivative. Sign changes can only occur when there are factors with odd powers, such as \((x+1)\) and \((x-1)\). These change sign at \(x=-1,1\), respectively - making both inflection points. There is NO sign change at \(x=0\), since the factor \(x^{2}\) is always positive.

Mastered Material Check

4. How might you determine sign changes for a function which is not given as product of factors?
5. Circle the places where the function depicted below changes sign.