7.2: Optimization with a constraint

Learning Objectives

1. Set up an optimization word problem involving formulae for volume and surface area of geometric solids.
2. Identify a constraint in an optimization problem.
3. Use the constraint to eliminate one of the independent variables, and find a desired critical point. (As before, this includes classifying the critical point as a local minimum, maximum or neither.)

In the next examples, identifying the function to optimize is part of the challenge. We also consider cases with more than one independent variable, where a constraint is used to eliminate all but one.

A cylindrical cell with minimal surface area

Not all cells are spherical. Some are cylindrical or sausage shaped. We explore how minimization of surface area would determine the overall shape of a cylindrical cell with a circular cross-section.

The volume of the cell is assumed to be fixed, because the cytoplasm in its interior cannot be "compressed". However, suppose that the cell has a "rubbery" membrane that tends to take on the smallest surface area possible. In physical language, the elastic energy stored in the membrane tends to a minimum. We want to find the proportions of the cylinder (that is, the ratio of length to radius) so that the cell has minimal surface area.

Figure 7.2: Properties of a cylinder

Recall the following properties for a cylinder of length \(L\) and radius \(r\) :

• The volume of a cylinder is the product of its base area, \(A\), and its height, \(L\). That is, \(V=A L\). For a cylinder with circular cross-section, \(V=\pi r^{2} L\).
• As in Figure 7.2, a cylinder can be "cut and unrolled" into a rectangle with side lengths \(L\) and \(2 \pi r\), where \(r\) is the radius of the circular cross-section. The surface area is the product of these side lengths, \(S_{\text {side }}=2 \pi r L\).
• If the "ends" of the cylinder are two flat circular caps then the sum of the areas of these two ends is \(S_{\text {ends }}=2 \pi r^{2}\). While in a real cell, the end caps would not be actually flat, for simplicity, we assume flat, circular ends.
• The total surface area of the cylinder with flat ends is then \[S=2 \pi r L+2 \pi r^{2} . \nonumber \]

Mastered Material Check

5. If a cylindrical cell has volume \(100 \mu \mathrm{m}^{3}\) and length \(10 \mu \mathrm{m}\), what is its radius?
6. What is the surface area of a cylindrical cell with volume \(100 \mu \mathrm{m}^{3}\) and length \(10 \mu \mathrm{m}\) ?

Mathematically, our problem can be restated as follows

Example 7.3

Minimize the surface area \(S=2 \pi r L+2 \pi r^{2}\) of the cell, given that its volume \(V=\pi r^{2} L=K\) is constant \({ }^{1}\).

Solution

The shape of the cell depends on both the length, \(L\), and the radius, \(r\), of the cylinder. However, these are not independent. They are related to one another because the volume of the cell has to be constant. This is an example of an optimization problem with a constraint, i.e., a condition that has to be satisfied. The constraint is "the volume is fixed", i.e.,

\[V=\pi r^{2} L=K, \nonumber \]

where \(K>0\) is a constant. This constraint allows us to eliminate one variables. For example, solving for \(L\), we have

\[L=\frac{K}{\pi r^{2}}\]

substituting this into the function \(S\) yields

\(S=2 \pi r L+2 \pi r^{2} . \Rightarrow S(r)=2 \pi r \frac{K}{\pi r^{2}}+2 \pi r^{2} \quad \Rightarrow \quad S(r)=2 \frac{K}{r}+2 \pi r^{2}\),

where \(S\) is now a function of a single independent variable, \(r\) ( \(K\) and \(\pi\) are constants).

We have formulated the mathematical problem: find the minimum of \(S(r)\).

We compute derivatives to find and classify the critical points:

\[S^{\prime}(r)=-2 \frac{K}{r^{2}}+4 \pi r, \quad S^{\prime \prime}(r)=4 \frac{K}{r^{3}}+4 \pi . \nonumber \]

Since \(K, r>0\), the second derivative is always positive, so \(S(r)\) is concave up. Any critical point we find is thus automatically a minimum. (In Exercise 7 we also consider the first derivative test as practice.) Setting \(S^{\prime}(r)=0\) :

\[S^{\prime}(r)=-2 \frac{K}{r^{2}}+4 \pi r=0 . \nonumber \]

Solving for \(r\), we obtain

\[2 \frac{K}{r^{2}}=4 \pi r \quad \Rightarrow \quad r^{3}=\frac{K}{2 \pi} \quad \Rightarrow \quad r=\left(\frac{K}{2 \pi}\right)^{1 / 3} . \nonumber \]

We can also find the length of this cell from Equation 7.2.1.

\[L=\left(\frac{4 K}{\pi}\right)^{1 / 3} . \nonumber \]

(Details are left for Exercise 7).

We can finally characterize the shape of the cell. One way is to specify the ratio of its radius to its length. Based on our previous results, we find that ratio to be:

\[\frac{L}{r}=2 \nonumber \]

(Exercise 7). This implies that \(L=2 r\) which coincides with the length of a diameter of the same circle.

This means the "cylindrical cell" with rubbery membrane would be short and fat - something almost like a sphere of radius \(r\) with flattened ends. Some cells do grow as long cylindrical filaments, but such growth is inconsistent with an elastic membrane or a minimal surface area. (In fact, filamentous growth is one way for cells to maximize their surface area, and reduce the challenge of absorbing nutrients.)

I would like to thank Prof Nima Geffen (Tel Aviv University) for providing the inspiration for this example.

Mastered Material Check

7. Redo Example \(7.3\) for a cell with fixed volume \(100 \mu \mathrm{m}^{3}\).

Wine for Kepler’s wedding

In 1613, Kepler set out to purchase a few barrels of wine for his wedding party. To compute the cost, the merchant would plunge a measuring rod through the tap hole, as shown in Figure \(7.3\) and measure the length \(L\) of the "wet" part of rod. The cost would be set at a value proportional to \(L\).

Kepler noticed that barrels come in different shapes. Some are tall and skinny, while others are squat and fat. He conjectured that some shapes would contain larger volumes for a given length \(L\), i.e. would contain more wine for the same price. Knowing mathematics, he set out to determine which barrel shape would be the best bargain for his wedding.

Figure 7.3: Barrels come in various shapes. But the cost of a barrel of wine was determined by the length \(L\) (dashed blue line segment) of the wet portion of the rod inserted into the tap hole. Kepler figured out which barrels contain the most wine for a given price.

Kepler sought the wine barrel that contains the most wine for a given cost. This is equivalent to asking which cylinder has the largest volume for a fixed (constant) length L. Below, we solve this optimization problem. An alternate approach is to seek the wine barrel that costs least for a given volume (Exercise 14), which leads to the same result.

Mastered Material Check

8. Give two different examples of barrel dimensions which would both yield a volume of 160L.

Example 7.4

Find the proportions (height:radius) of the cylinder with largest volume for a fixed length L (dashed line segment in Figure 7.3).

Solution

We make the following assumptions:

1. the barrel is a simple cylinder, as shown in Figure \(7.4\),
2. the tap-hole (normally sealed to avoid leaks) is half-way up the height of the barrel, and
3. the barrel is full to the top with wine.

Let \(r, h\) denote the radius and height of the barrel. These two variables uniquely determine the shape as well as the volume of the barrel. Note that because the barrel is assumed to be full, the volume of the cylinder is the same as the volume of wine, namely

\[V=\text { base area } \times \text { height. } \Rightarrow V=\pi r^{2} h \]

Figure 7.4: We simplify the problem to a cylindrical barrel with diameter \(2 r\) and height \(h\). We assumed that the height of the tap-hole is \(h / 2\). Length \(L\) denotes the "wet" portion of the merchant’s rod, used to determine the cost. We observe a Pythagorean triangle formed by the dashed line segments.

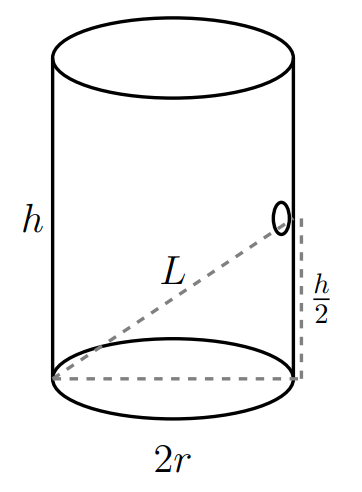
The rod used to "measure" the amount of wine (and hence determine the cost of the barrel) is shown as the diagonal of length \(L\) in Figure 7.4. Because the cylinder walls are perpendicular to its base, the length \(L\) is the hypotenuse of a right-angle triangle whose other sides have lengths \(2 r\) and \(h / 2\). (This follows from the assumption that the tap hole is half-way up the side.) Thus, by the Pythagorean theorem,

\[L^{2}=(2 r)^{2}+\left(\frac{h}{2}\right)^{2} \]

The problem can now be stated mathematically: maximize \(V\) in Equation (7.2.2) subject to a fixed value of \(L\) in Equation (7.2.3). The fact that \(L\) is fixed means that we have a constraint, as before, that we use to reduce the number of variables in the problem.

Expanding the squares in the constraint and solving for \(r^{2}\) leads to

\[L^{2}=4 r^{2}+\frac{h^{2}}{4} \quad \Rightarrow \quad r^{2}=\frac{1}{4}\left(L^{2}-\frac{h^{2}}{4}\right) . \nonumber \]

When we use this to eliminate \(r\) from the expression for \(V\), we obtain

\[V=\pi r^{2} h=\frac{\pi}{4}\left(L^{2}-\frac{h^{2}}{4}\right) h=\frac{\pi}{4}\left(L^{2} h-\frac{1}{4} h^{3}\right) \nonumber \]

The mathematical problem to solve is now: find \(h\) that maximizes

\[V(h)=\frac{\pi}{4}\left(L^{2} h-\frac{1}{4} h^{3}\right) . \nonumber \]

The function \(V(h)\) is positive for \(h\) in the range \(0 \leq h \leq 2 L\), and \(V=0\) at the two endpoints of the interval. We can restrict attention to this interval since otherwise \(V<0\), which makes no physical sense. Since \(V(h)\) is a smooth function, we anticipate that somewhere inside this range of values there should be a maximal volume.

Computing first and second derivatives, we find

\[V^{\prime}(h)=\frac{\pi}{4}\left(L^{2}-\frac{3}{4} h^{2}\right), \quad V^{\prime \prime}(h)=\frac{\pi}{4}\left(0-2 \cdot \frac{3}{4} h\right)=-\frac{3}{8} \pi h<0 . \nonumber \]

Setting \(V^{\prime}(h)=0\) to find critical points, we then solve for \(h\) :

\[\begin{aligned} V^{\prime}(h)=0 \quad & \Rightarrow \quad L^{2}-\frac{3}{4} h^{2}=0 \quad \Rightarrow \quad 3 h^{2}=4 L^{2} \\ & \Rightarrow \quad h^{2}=4 \frac{L^{2}}{3} \quad \Rightarrow \quad h=2 \frac{L}{\sqrt{3}} . \end{aligned} \nonumber \]

We verify that this solution is a local maximum by the following reasoning.

The second derivative \(V^{\prime \prime}(h)=-\frac{3}{8} \pi h<0\) is always negative for any positive value of \(h\), so \(V(h)\) is concave down for \(h>0\), which confirms a local maximum. We also noted that \(V(r)\) is smooth, positive within the range of interest and zero at the endpoints. As there is only one critical point in that range, it must be a local maximum.

Finally, we find the radius of the barrel by plugging the optimal \(h\) into the constraint equation, i.e. using

\[\begin{gathered} r^{2}=\frac{1}{4}\left(L^{2}-\frac{h^{2}}{4}\right)=\frac{1}{4}\left(L^{2}-\frac{L^{2}}{3}\right)=\frac{1}{4}\left(\frac{2}{3} L^{2}\right) \\ \Rightarrow \quad r=\frac{1}{\sqrt{3} \sqrt{2}} L . \end{gathered} \nonumber \]

The shape of the optimal barrel can now be characterized. One way to do so is to specify the ratio of its height to its radius. (Tall skinny barrels have a large \(h / r\) ratio, and squat fat ones have a low ratio.) By the above reasoning, the ratio of \(h / r\) for the optimal barrel is

\[\frac{h}{r}=\frac{2 \frac{L}{\sqrt{3}}}{\frac{1}{\sqrt{3} \sqrt{2}} L}=2 \sqrt{2} \]

Hence, for greatest economy, Kepler would have purchased barrels with height to radius ratio of \(2 \sqrt{2}=2.82 \approx 3\).

Mastered Material Check

9. If all barrels had a radius of \(25 \mathrm{~cm}\), given the result Example 7.4, what would be the best barrel height?
10. What would the volume of such a barrel be?
11. Consider a barrel with radius \(25 \mathrm{~cm}\) and height \(100 \mathrm{~cm}\). What is this barrel’s volume?