9.1: Applications of the Chain Rule to “Related Rates”

Learning Objectives

1. Given a geometric relationship and a rate of change of one of the variables, use the chain rule to find the rate of change of a related variable.
2. Use descriptive information about rates of change to set up the required relationships, and to solve a word problem involving an application of the chain rule ("related rates problem").

See A brief introduction

In many applications of the chain rule, we are interested in processes that take place over time. We ask how the relationships between certain geometric (or physical) variables affects the rates at which they change over time. Many of these examples are given as word problems, and we must assemble the required relationships to solve the problem. Some useful geometric relationships are presented in Table \(9.1\).

Table 9.1: Geometric relationships used in various related rates problems.

Volume of sphere	\(V=\frac{4}{3} \pi r^3\)
Surface area of sphere	\(S=4 \pi r^2\)
Area of circle	\(A=\pi r^2\)
Perimeter of circle	\(P=2 \pi r\)
Volume of cylinder	\(V=\pi r^2 h\)
Volume of cone	\(V=\frac{1}{3} \pi r^2 h\)
Area of rectangle	\(A=x y\)
Perimeter of rectangle	\(P=2 x+2 y\)
Volume of box	\(V=x y z\)
Sides of right triangle	\(c^2=a^2+b^2\)

Example 9.1 (Tumor growth)

The radius of a solid tumor expands at a constant rate, \(k\). Determine the rate of growth of the volume of the tumor when the radius is \(r=1 \mathrm{~cm}\). Assume that the tumor is approximately spherical as depicted in Figure 9.1.

Figure 9.1: Growth of a spherical tumor. Since the radius changes with time, the volume, too, changes with time. We use the chain rule to link \(d V / d t\) to \(d r / d t\).

Solution

The volume of a sphere of radius \(r\), is \(V(r)=(4 / 3) \pi r^{3}\). Here, \(r\) changes with time, so \(V\) changes with time. We indicate this chain of dependencies with the notation \(r(t)\) and \(V(r(t))\). Then function composition is apparent:

\[V(r(t))=\frac{4}{3} \pi[r(t)]^{3} \nonumber \]

Then, using the chain rule,

\[\frac{d}{d t} V(r(t))=\frac{d V}{d r} \frac{d r}{d t}=\frac{d}{d r}\left(\frac{4}{3} \pi r^{3}\right) \frac{d r}{d t}=\frac{4}{3} \pi \cdot 3 r^{2} \frac{d r}{d t}=4 \pi r^{2} \frac{d r}{d t} \nonumber \]

But we are told that the radius expands at a constant rate, \(k\), so that

\[\frac{d r}{d t}=k . \quad \Rightarrow \quad \frac{d V}{d t}=4 \pi r^{2} k \nonumber \]

Hence, the rate of growth of the volume is proportional to the square of the radius; in fact, it is proportional to the surface area of the sphere. At the instant that \(r=1 \mathrm{~cm}\),

\[\frac{d V}{d t}=4 \pi k . \nonumber \]

Importantly, the numerical value \(r=1 \mathrm{~cm}\) holds only at one instant and is used at the end of the calculation, after the differentiation and simplification steps are completed.

Featured Problem 9.1 (Growth of a cell): The mass of a cell is \(m=\rho V\) where \(V\) is cell volume and \(\rho\) is cell density. (Usually, cell density is constant and close to that of water, \(\rho \approx 1 \mathrm{~g} / \mathrm{cm}^{3}\).) Relate the cell rate of change of mass to rate of change of volume and to rate of change of radius. Assume that the cell is spherical.

Tumor growth example: See the calculation in action.

Mastered Material Check

1. What is \(d V / d t\) when the radius is \(r=2 \mathrm{~cm}\) ?
2. What are the units of \(d V / d t\) ?

Example 9.2 (Convergent extension)

Most animals are longer head to tail than side to side. To obtain relative elongation along one axis, an embryo undergoes a process called convergent extension whereby a block of tissue elongates (extends) along one axis and narrows (converges) along the other axis as shown in Figure 9.2. Here we consider this process.

Suppose that a rectangular block of tissue, with dimensions \(L=w=10 \mathrm{~mm}\) and thickness \(\tau=1 \mathrm{~mm}\), extends at the rate of \(1 \mathrm{~mm}\) per day, while the volume \(V\) and thickness \(\tau\) remain fixed. At what rate is the width \(w\) changing when the length is \(L=20 \mathrm{~mm}\) ?

Figure 9.2: Convergent extension of tissue in embryonic development. Cells elongate along one axis (which increases \(L\) ) while contracting along the other axis (decreasing w). Since the volume and thickness remain fixed, the changes in \(L\) can be related to changes in \(w\).

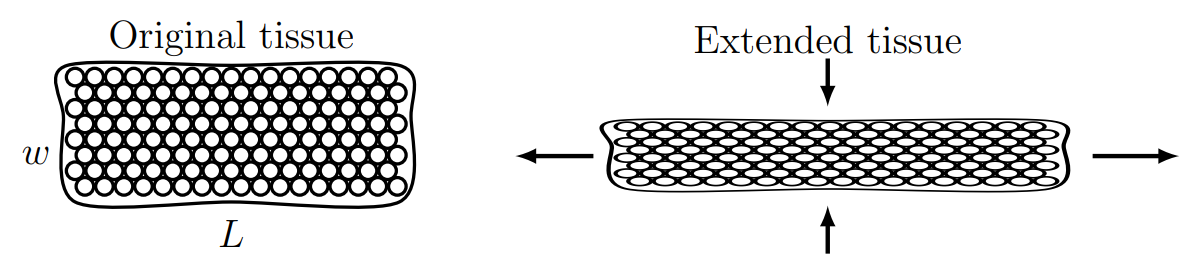
Solution

We are told that the volume \(V\) and the thickness \(\tau\) remain constant. We find, using the initial length, width and thickness, that the volume is \(V=10 \cdot 10 \cdot 1 \mathrm{~mm}^{3}\). Further, at any given time \(t\), the volume of the rectangular block is

\[V=L(t) \cdot w(t) \cdot \tau . \nonumber \]

\(V\) depends on \(L\) and \(w\), both of which depend on time. Hence, there is a chain of dependencies \(t \rightarrow L, w, \rightarrow V\), Differentiating both sides with respect to \(t\) leads to

\[\frac{d V}{d t}=\frac{d}{d t}(L(t) \cdot w(t) \tau) \quad \Rightarrow \quad 0=\left(L^{\prime}(t) \cdot w(t)+L(t) \cdot w^{\prime}(t)\right) \tau \nonumber \]

(Here we have used the product rule to differentiate \(L(t) \cdot w(t)\) with respect to \(t\). We also used the fact that \(V\) is constant so its derivative is zero, and \(\tau\) is constant, so it multiplies the derivative of \(L(t) w(t)\) as would any multiplicative constant.) Consequently, canceling the constant factor and solving for \(w^{\prime}(t)\) results in

\[L^{\prime}(t) w(t)+L(t) w^{\prime}(t)=0 \quad \Rightarrow \quad w^{\prime}(t)=-\frac{L^{\prime}(t) w(t)}{L(t)} \nonumber \]

At the instant that \(L(t)=20, w(t)=V /(L(t) \tau)=100 / 20=5\). Hence we find that

\[w^{\prime}(t)=-\frac{L^{\prime}(t) w(t)}{L(t)}=-\frac{1 \mathrm{~mm} / \text { day } \cdot 5 \mathrm{~mm}}{20 \mathrm{~mm}}=-0.25 \mathrm{~mm} / \text { day } \nonumber \]

The negative sign indicates that \(w\) is decreasing while \(L\) is increasing.

Mastered Material Check

3. How wide is the tissue when \(L=20 \mathrm{~mm}\) if thickness \(\tau\) and volume \(V\) remain fixed?

Example 9.3 (A spider’s thread)

A spider moves horizontally across the ground at a constant rate, \(k\), pulling a thin silk thread with it. One end of the thread is tethered to a vertical wall at height h above ground and does not move. The other end moves with the spider. Determine the rate of elongation of the thread.

Solution

Figure 9.3: The length of a spider’s thread.

Figure \(9.3\) illustrates the geometry, where \(x\) is the distance of the spider from the wall. We use the Pythagorean Theorem to relate the height of the tether point \(h\), the spider’s location \(x\), and the length of the thread \(\ell\) :

\[\ell^{2}=h^{2}+x^{2} . \nonumber \]

Here, \(h\) is constant, while \(x, \ell\) change with time, so that

\[[\ell(t)]^{2}=h^{2}+[x(t)]^{2} . \nonumber \]

Differentiating with respect to \(t\) leads to

\[\begin{gathered} \frac{d}{d t}\left([\ell(t)]^{2}\right)=\frac{d}{d t}\left(h^{2}+[x(t)]^{2}\right), \\ 2 \ell \frac{d \ell}{d t}=0+2 x \frac{d x}{d t} \Rightarrow \frac{d \ell}{d t}=\frac{2 x}{2 \ell} \frac{d x}{d t} . \end{gathered} \nonumber \]

Simplifying and using the fact that

\[\frac{d x}{d t}=k \nonumber \]

leads to

\[\frac{d \ell}{d t}=\frac{x}{\ell} k=k \frac{x}{\sqrt{h^{2}+x^{2}}} \nonumber \]

Mastered Material Check

4. Repeat Example \(9.3\) given that the thread is tethered \(0.5 \mathrm{~m}\) above the ground and the spider is walking at a constant rate of \(30 \mathrm{~cm} / \mathrm{min}\).

A Spider silk example: See the calculation in action.

Example 9.4 (A conical cup)

Water is leaking at a constant rate out of a conical cup of height \(H\) and radius \(R\). Find the rate of change of the height of water in the cup at the instant that the cup is full, if the volume is decreasing at a constant rate, \(k\).

Figure 9.4: The geometry of a conical cup of (constant) height \(H\) and (constant) radius \(R\). The surface of the water is indicated with dashed line. The water occupies a conical volume of height \(h(t)\) and radius \(r(t)\), which both get smaller as waters leaks out of the cup. The diagram on the left strongly suggests that similar triangles would be helpful in finding a relationship between the variables.

Solution

Let us define \(h\) and \(r\) as the height and radius of water inside the cone. Then we know that the volume of this (conically shaped) water in the cone is

\[V=\frac{1}{3} \pi r^{2} h \nonumber \]

or, in terms of functions of time,

\[V(t)=\frac{1}{3} \pi[r(t)]^{2} h(t) . \nonumber \]

We are told that

\[\frac{d V}{d t}=-k, \nonumber \]

where the negative sign indicates that volume is decreasing. By similar triangles, we note that

\[\frac{r}{h}=\frac{R}{H} \quad \Rightarrow \quad r=\frac{R}{H} h, \nonumber \]

so we use this substitution to write the volume in terms of the height alone:

\[V(t)=\frac{1}{3} \pi\left[\frac{R}{H}\right]^{2}[h(t)]^{3} \nonumber \]

Then the chain rule leads to

\[\frac{d V}{d t}=\frac{1}{3} \pi\left[\frac{R}{H}\right]^{2} \cdot 3[h(t)]^{2} \frac{d h}{d t} \nonumber \]

Now using the fact that volume decreases at a constant rate, we get

\[-k=\pi\left[\frac{R}{H}\right]^{2}[h(t)]^{2} \frac{d h}{d t} \Rightarrow \frac{d h}{d t}=\frac{-k H^{2}}{\pi R^{2} h^{2}} \nonumber \]

The rate computed above holds at any time as the water leaks out of the container. At the instant that the cup is full, \(h(t)=H\) and \(r(t)=R\), so that

\[\frac{d h}{d t}=\frac{-k H^{2}}{\pi R^{2} H^{2}}=\frac{-k}{\pi R^{2}} . \nonumber \]

For example, for a cone of height \(H=4\) and radius \(R=3\),

\[\frac{d h}{d t}=\frac{-k}{9 \pi} \nonumber \]

It is important to use information about a specific instant only after derivatives are computed.

Draining Cone Example: See the calculation in action.

Mastered Material Check

5. What volume of water can be contained in a cone of height \(5 \mathrm{~cm}\) and radius \(3 \mathrm{~cm}\) ?
6. What are the units of the constant \(k\) ?
7. What is meant by similar triangles?

Featured Problem \(9.2\) (Growth of a Tree Trunk): Consider a cylindrical tree trunk of radius \(R\). Living cells occupy a thin shell (thickness d) just inside the tree bark. The interior of the trunk consists of dead cells that have turned into wood.

Figure 9.5: A thin shell of living tissue (phloem) surrounds the dead wooden part of a tree trunk (xylem). The fraction \(F\) of living tissue changes as the tree grows.

1. What fraction \(F\) of the trunk volume is living tissue?
2. How does the fraction \(F\) change with time as the tree grows? Assume that the radius of the trunk grows at a constant rate, and that the thickness \(d\) does not change. Compute the rate of change of \(F\) at the instant that the radius is 5 times the thickness \(d\).

Figure 9.6: The radius of the trunk is \(R\) and the thickness of the phloem (living part of the trunk) is \(d\). We assume a cylindrical geometry. \(F\) = fraction of volume in the thin (blue) cylindrical shell.

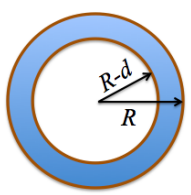
An explanation of how to set up the tree trunk problem.

Some further steps, and an outline of what we are asked to do.

Hints and setting up the problem

• Assume that the wooden interior is cylindrical, as is the trunk. Find the volume of the shell by subtracting the volumes of these two cylinders, and now write down the fraction \(F\). You should get \[F=\frac{\pi h\left[R^{2}-(R-d)^{2}\right]}{\pi h R^{2}} \nonumber \] Simplify this expression.
• Compute the derivative \(d F / d t\), remembering to use the Chain Rule. You may want to use the quotient rule for practice, or to first simplify the expression as much as possible and then compute a derivative.