14: Periodic and Trigonometric Functions

Last updated
Save as PDF

Page ID: 121156

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Nature abounds with examples of cyclic processes. Perhaps most familiar is the continually repeating heartbeat that accompanies us through life. Electrically active muscles power the heart. That electrical activity can be recorded on the surface of the body by an electrocardiogram (ECG), as shown in Figure 14.1. In a normal healthy human at rest, the electrical activity pattern associated with a complete cycle repeats itself with roughly 1 heartbeat per second. At exercise, the beating heart pumps faster, so the pattern repeats more frequently.

To study the behavior shown in Figure 14.1, we must first develop language that describes such periodic phenomena. For example, we need to quantify what is meant by "more frequent repetition" of a heart beat, "skipping a beat," or other shifts in the pattern of this or of any other cycling system.

Figure 14.1: An electrocardiogram (ECG) shows the pattern of electrical activity of the heart. Vertical axis: millivolts, horizontal axis: time in seconds. At rest (top), the heart beats approximately 60 times per minute, but in exercise (lower trace), the heart rate increases.

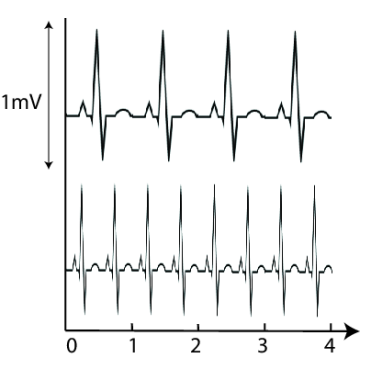
Before trying to understand intricate examples such as ECG’s, we begin with simple prototypes of periodic functions: the trigonometric functions, sine and cosine. Belonging to a wider class of periodic functions, these cases illustrate ideas of amplitude, frequency, period, and phase. Many cyclic phenomena can be described approximately by suitably adjusting such basic functions. Our study in this elementary context then aids in the goal of analyzing periodic functions in general - and periodicity of the ECG’s in particular (we return to this in Example 14.2).

As a second theme, we return to inverse functions and show that restrictions must be applied to ensure the existence of an inverse, particularly for trigonometric functions. Then, in Chapter 15 , we calculate the derivatives of trigonometric functions and explore applications to rates of change of periodic phenomena or changing angles.