14.1: Basic Trigonometry

Learning Objectives

1. Define radian as a measure for angles.
2. Describe the correspondence between a point moving on a unit circle and the sine and cosine of the angle it forms at the origin.
3. Make correspondence between ratios of sides of a Pythagorean triangle and the trigonometric functions of one of its angles.
4. Review properties of the functions \(\sin (x)\) and \(\cos (x)\) and other trigonometric functions. State and apply the connections between these functions ("trigonometric identities").

Trigonometric functions are closely associated with angles and ratios of sides of a right-angle triangle. They are also connected to the motion of a point moving around a unit circle. Before we articulate these connections, we must agree on a universal way of measuring angles.

Angles and circles

Angles can be measured in a number of ways. One is to assign a value in degrees, with the convention that one complete revolution is represented by \(360^{\circ}\). It turns out that this measure is not particularly convenient, and we instead replace it with a more universal quantity.

Figure 14.2: Circumference, diameter and radius of a circle.

Our definition of angles will be based on the fact that circles of all sizes have one common geometric feature: they have the same ratio of circumference, to diameter, no matter what their size (or where in the universe they occur). We call that ratio \(\pi\), that is

\[\pi=\frac{\text { Circumference of circle }}{\text { Diameter of circle }} . \nonumber \]

By construction, the diameter \(D\) of a circle is a distance that corresponds to twice the radius \(R\) of that circle, so

\[D=2 R \text {. } \nonumber \]

This leads to the familiar relationship of circumference \(C\), to radius \(R\),

\[C=2 \pi R . \nonumber \]

This statement is merely a definition of the constant \(\pi\).

Figure 14.3: The angle \(\theta\) in radians is related to the radius \(R\) of the circle, and the length of the \(\operatorname{arc} S\) by the simple formula, \(S=R \theta\).

As shown in Figure 14.3, an angle \(\theta\) can be put into correspondence with an arc along the edge of a circle. For a circle of radius \(R\) and angle \(\theta\) we define the arclength, \(S\) by the relation \(S=R \theta\) where \(\theta\) is measured in a convenient way that we now select. Both \(S\) and \(R\) carry units of "distance" or "length". But their ratio is,

\[\theta=\frac{S}{R}, \nonumber \]

so the units in numerator and denominator cancel, and the angle \(\theta\) is dimensionless (carries no units).

Now consider a circle of radius \(R=1\) (called a unit circle) and denote by \(s\) a length of arc around the entire perimeter of this unit circle. Then

\[\theta=\frac{s}{1} . \nonumber \]

In particular, for one complete revolution around the circle, the arclength is \(s=2 \pi \cdot 1=2 \pi\), which is just the circumference of the unit circle. In that case, it makes sense to consider the angle corresponding to one revolution as

\[\theta=\frac{2 \pi}{1}=2 \pi . \nonumber \]

This leads naturally to the definition of the radian: we identify an angle of \(2 \pi\) radians with one complete revolution around the circle. Note that (like degrees or other measures of angles), a radian is a number that carries no "units".

We can now use this measure for angles to assign values to any fraction of a revolution, and thus, to any angle. For example, an angle of \(90^{\circ}\) corresponds to one quarter of a revolution around the perimeter of a unit circle, so we identify the angle \(\pi / 2\) radians with it. One degree is \(1 / 360\) of a revolution, corresponding to \(2 \pi / 360\) radians, and so on.

We summarize the properties of radians:

1. The length of an arc along the perimeter of a circle of radius \(R\) corresponding to an angle \(\theta\) between two radii is \(S=R \theta\) for \(\theta\) in radians.
2. An angle in radians is the ratio of the arclength it subtends in a circle to the radius of that circle (and hence, a radian carries no units).
3. One complete revolution, or one full cycle corresponds to an angle of \(2 \pi\) radians.

We can convert between degrees and radians by remembering that \(360^{\circ}\) corresponds to \(2 \pi\) radians \(\left(180^{\circ}\right.\) then corresponds to \(\pi\) radians, \(90^{\circ}\) to \(\pi / 2\) radians, etc.)

Mastered Material Check

1. What angle \(\theta\) corresponds to a \(1 / 6\) revolution around the perimeter of a circle?
2. Sketch an angle of \(\pi / 4\) radians.
3. If the radius of a circle is 2 and an arc on its perimeter has length \(0.5\), what is the angle corresponding to that arc (in radians)?

Defining the trigonometric functions \(\sin (t)\) and \(\cos (t)\)

Consider a point \((x, y)\) moving around the rim of a circle of radius 1 , and let \(t\) be some angle (measured in radians) formed by the \(x\)-axis and the radius vector to the point \((x, y)\) as shown in Figure 14.4.

Figure 14.4: The equation of a circle of radius 1 , with center at the origin is \(x^{2}+y^{2}=1\). The radius vector to the point \((x, y)\) forms an angle \(t\) (radians) with the \(x\)-axis. In the triangle, shown enlarged on the right, lengths of sides are labeled. The trigonometric functions are just ratios of two sides of this triangle.

Mastered Material Check

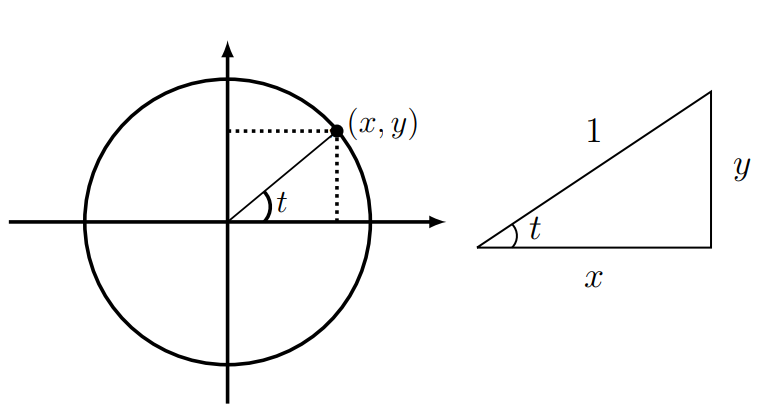
4. How many radians does \(270^{\circ}\) correspond to?
5. Label \(\cos (t)\) and \(\sin (t)\) where appropriate on Figure 14.4.

We define the functions sine and cosine, both dependent on the angle \(t\) (abbreviated \(\sin (t)\) and \(\cos (t)\) ) as follows:

\[\sin (t)=\frac{y}{1}=y, \quad \cos (t)=\frac{x}{1}=x \nonumber \]

That is, the function sine tracks the y coordinate of the point as it moves around the unit circle, and the function cosine tracks its \(x\) coordinate.

Note: A review and definitions of trigonometric quantities is given in Figure F.1, Appendix F as ratios of sides in a right angle triangle. The hypotenuse in our diagram is simply the radius \(r=1\) of the circle.

Featured Problem \(14.1\) (Cosine as motion around circle): Adapt the interactive sine graph to represent the link between the graph of \(y=\cos (x)\) and the \(x\) coordinate of a point moving around a circle.

A demonstration of the link between motion on a circle and the function \(y=\sin (x)\). Click on the arrow left of the parameter \(a\) or shift the slider on \(a\) to see the moving point.

Properties of \(\sin (t)\) and \(\cos (t)\)

We now explore the consequences of these definitions:

Values of sine and cosine

• The radius of the unit circle is 1 . This means that the \(x\) coordinate of any point \((x, y)\) on the unit circle cannot be larger than 1 or smaller than \(-1\). The same holds for the \(y\) coordinate. Thus, the functions \(\sin (t)\) and \(\cos (t)\) are always swinging between \(-1\) and 1. \((-1 \leq \sin (t) \leq 1\) and \(-1 \leq\) \(\cos (t) \leq 1\) for all angles \(t\) ). The maximum value of each function is 1 , the minimum is \(-1\), and the average is 0 .
• We adopt the convention that when the radius vector points along the \(x\)-axis, the angle is \(t=0\), and coordinates of the point are \(x=1, y=0\). This implies that \(\cos (0)=1, \sin (0)=0\).
• When the radius vector points up the \(y\)-axis, the angle is \(\pi / 2\) (corresponding to one quarter of a complete revolution), and coordinates of the point are \(x=0, y=1\) so that \(\cos (\pi / 2)=0, \sin (\pi / 2)=1\).
• Through geometry, we can also determine the lengths of all sides - and hence the ratios of the sides - of particular triangles, namely
  • equilateral triangles (in which all angles are \(60^{\circ}\) ), and
  • right triangles (two equal angles of \(45^{\circ}\) ).

These types of calculations (omitted here) lead to some easily determined values for the sine and cosine of such special angles. These are shown in Table F.1 of the Appendix F.

Characteristics of sine and cosine

• Both \(\sin (t)\) and \(\cos (t)\) go through the same values every time the angle \(t\) completes another cycle around the circle. We refer to such functions as periodic functions.
• The two functions, sine and cosine depict the same underlying motion, viewed from two perspectives: \(\cos (t)\) represents the projection of the circularly moving point onto the \(x\)-axis, while \(\sin (t)\) is the projection of the same point onto the \(y\)-axis. In this sense, the functions are "twins", and as such we expect many relationships connecting them.
• The cosine has its largest value at the beginning of the cycle, when \(t=0\) \((\) since \(\cos (0)=1)\), while sine has its peak value a little later \((\sin (\pi / 2)=\) 1). Throughout their circular race, the sine function is \(\pi / 2\) radians ahead of the cosine, that is, \[\cos (t)=\sin \left(t+\frac{\pi}{2}\right) \nonumber \] See Figure \(14.5\) for graphs of both functions showing this shift by \(\pi / 2\).
• The period \(T\) of the sine function \(\sin (t)\) is defined as the value of \(t\) for which one whole cycle (around the circle) has been completed. Accordingly, this period is \(T=2 \pi\). Similarly the period of the cosine function \(\cos (t)\) is also \(2 \pi\). (See Figure 14.5.)

Figure 14.5: Periodicity of the sine and cosine. Note that the two curves are just shifted versions of one another.

• The point \((x, y)=(\cos (t), \sin (t))\) is on a circle of radius 1 , and, thus, its coordinates satisfy \[x^{2}+y^{2}=1 \nonumber \] This implies that \[\sin ^{2}(t)+\cos ^{2}(t)=1 \] for any angle \(t\). This is an important relation, (also called a trigonometric identity), and one that is frequently used. See Appendix F for a review of other trigonometric identities.
• The sine and cosine functions have symmetries that we already encountered: \(\sin (t)\) is an odd function (symmetric about the origin) and the \(\cos (t)\) is an even function (symmetric about the \(y\)-axis). These symmetries also imply that \(\sin (-t)=-\sin (t)\) and \(\cos (-t)=\cos (t)\).

Mastered Material Check

6. Review Appendix \(\mathrm{F}\) and then use triangles to determine the \(x\) and \(y\) coordinates of angles of \(60^{\circ}\) and \(45^{\circ}\) in the unit circle.
7. Why does cosine have its largest value when the angle \(t=0\), at the beginning of the cycle?

Other trigonometric functions

Although we shall mostly be concerned with the two basic functions described above, several others are historically important and are encountered frequently in integral calculus. These include the following:

\[\begin{aligned} & \tan (t)=\frac{\sin (t)}{\cos (t)}, \cot (t)=\frac{1}{\tan (t)}, \\ & \sec (t)=\frac{1}{\cos (t)}, \quad \csc (t)=\frac{1}{\sin (t)} . \end{aligned} \nonumber \]

We review these and the identities that they satisfy in Appendix F. We also include the Law of Cosines in Equation (F.2), and angle-sum identities in the same appendix. Sine and cosine are the functions we focus on here.

You can use this desmos graph to see all the trigonometric functions. Turn the graphs on or off by clicking on the (grey) circles to the left of the formulae. Notice the vertical asymptotes on some of these functions and think about where these asymptotes occur. Although we shall mostly be concerned with the two basic functions d