4.4: Homework- Second Derivatives and Interpreting the Derivative
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Given each
- Let
- Let
- Let
- Let
- Let
- Let
- For each of the functions below, compute the derivative twice. That is, compute
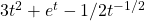 ,
, 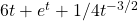 ans
ans- ans
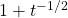 ,
, 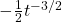 ans
ans
- For each graph, circle any inflection points (if any). Label each region between the inflection points has having either a positive or negative second derivative.
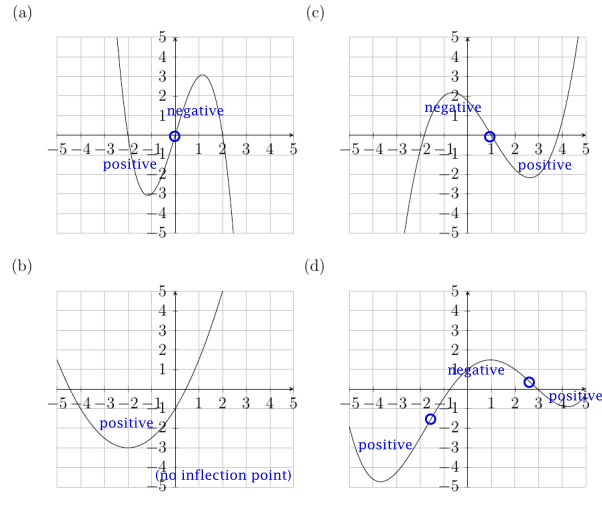 ans
ans - A river bank is eroding. Let
- What is
- Sketch the derivative.
- Find the derivative
ans
- How quickly is material being lost on day
- What is
- The stock price for Math Nerds, Inc, over the course of an 8 hour trading day (
- What is
- Sketch the graph of
- Compute
- How quickly is the stock gaining in price at
- At
- What is
- A tank has
- Sketch the graphs of
- What is
- Sketch the graphs of


