1.4: Arc Length

We can find the arc length of a curve by cutting it up into tiny pieces and adding up the length of each of the pieces. If the pieces are small and the curve is differentiable then each piece will be approximately linear.

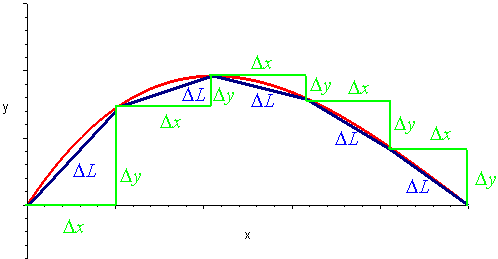
We can use the distance formula to find the length of each piece:

$$L = \sqrt{ \left(\Delta{x}\right)^2+ \left(\Delta{y}\right)^2}. \nonumber$$

Multiplying and dividing by $\Delta{t}$ gives

$$L = \sqrt{ \left(\dfrac{\Delta{x}}{\Delta{t}}\right)^2+ \left(\dfrac{\Delta{y}}{\Delta{t}}\right)^2} \, \Delta {t}. \nonumber$$

Adding up all the lengths and taking the limit as $\Delta{t}$ approaches 0 gives the formula

$$L = \int _a^b {\sqrt{ \left(\frac{dx}{dt}\right)^2+ \left(\frac{dy}{dt}\right)^2} \, dt}. \nonumber$$

Example $\PageIndex{1}$

Find the arc length of the curve defined parametrically by $x(t) = t^2 + 4t$ and $y(t) = 1 - t^2,$ from $0 < t < 2$.

Solution

We calculate the derivatives:

$$x' = 2t + 4 \;\;\; \text{and}\;\;\; y' = -2t. \nonumber$$

Hence, the integrand to integrate is

$$\sqrt{ \left(\dfrac{dx}{dt}\right)^2+ \left(\dfrac{dy}{dt}\right)^2} = \sqrt{ 8\,t^2 + 16\, t + 16} \nonumber$$

and the full integral to solve, with limits,

$$\int_0^2 \sqrt{ 8\,t^2 + 16\, t + 16} \, dt \nonumber$$

is difficult (but not impossible) to do by hand. Either by hand or by computer we get

$$L \approx 12.74. \nonumber$$

Larry Green (Lake Tahoe Community College)

• Integrated by Justin Marshall.