Smooth Vector-Valued Functions
- Last updated
- Dec 21, 2020
- Save as PDF
- Page ID
- 10924
( \newcommand{\kernel}{\mathrm{null}\,}\)
Definition: smoothness
Let ⇀r(t)=f(t)ˆi+g(t)ˆj+h(t)ˆk be the parameterization of a curve that is differentiable on an open interval I.
Then ⇀r(t) is smooth on the open interval I, if
⇀r′(t)≠⇀0, for any value of t in the interval I.
To put this another way, ⇀r(t) is smooth on the open interval I if:
- ⇀r(t) is defined and continuous on I, and
- f′,g′ and h′ are all continuous on I, that is, ⇀r′(t) is defined and continuous on I, and
- ⇀r′(t)≠⇀0 for all values of t in the interval I.
The concept of smoothness is very closely connected to the application of vector-valued functions to motion. If you have ever ridden rides at an amusement park, you can probably identify some where the ride felt smooth, and others where there are moments during the ride where it was not smooth. These moments often correspond to points in the motion where the relevant parameterization is not smooth by the definition above.
To identify open intervals in the domain of ⇀r on which ⇀r is smooth, we usually identify values of t for which ⇀r is not smooth.
In addition to using the definition above to identify these points, it is often apparent from the graph of the vector-valued function ⇀r(t). A cusp, i.e., a sharp turning point, is a common occurrence at points where a curve is not smooth. In Figure 3 below, you can quickly identify points at which the parameterization fails to be smooth by locating cusps in the graph.
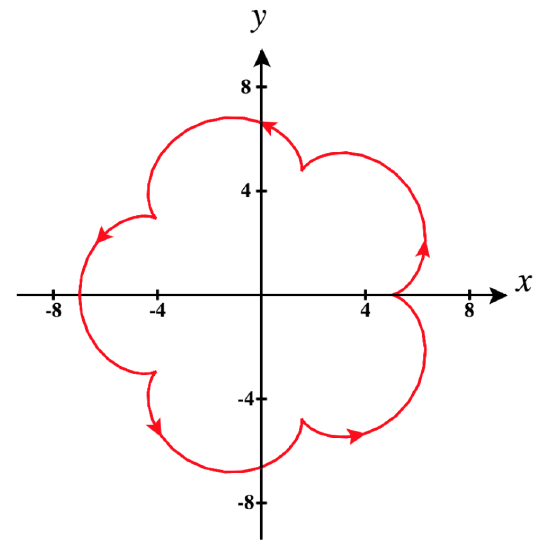
When we consider the motion described by ⇀r(t), there are at least two additional events that can occur at points where the parameterization fails to be smooth: a reversal of motion or a momentary pause in the motion. To summarize these events:
If a vector-valued function ⇀r(t) is not smooth at time t, we will observe that:
- There is a cusp at the associated point on the graph of ⇀r(t), or
- The motion reverses itself at the associated point, causing the motion to travel back along the same path in the opposite direction, or
- The motion actually stops and starts up again, with no visual cue, that is, where the curve appears smooth.
Let's consider a couple examples to see how this can look.
Example 4: Determining open intervals on which a vector-valued function is smooth
Determine the open intervals on which each of the following vector-valued functions is smooth:
- ⇀r(t)=(2t3−3t2)ˆi+(t2−2t)ˆj+2ˆk
- ⇀r(t)=t3ˆi+√t2−1ˆj
- ⇀r(t)=t4ˆi+ln(t2+1)ˆj
- ⇀r(t)=(6cost−cos(6t))ˆi+(6sint−sin(6t))ˆj, for 0≤t≤2π
Solution
a. First we need to consider the domain of ⇀r. In this case, D⇀r:(−∞,∞).
Then we need to find ⇀r′(t). Since ⇀r(t)=(2t3−3t2)ˆi+(t2−2t)ˆj+2ˆk,
⇀r′(t)=(6t2−6t)ˆi+(2t−2)ˆj
Next we need to consider the domain of ⇀r′. Here, D⇀r′:(−∞,∞).
Finally we need to determine if there are any values of t in D⇀r where ⇀r′(t)=⇀0.
To do this, we set each component of ⇀r′(t) equal to 0 and solve for t.
6t2−6t=0and2t−2=06t(t−1)=02(t−1)=0t=0ort=1t=1
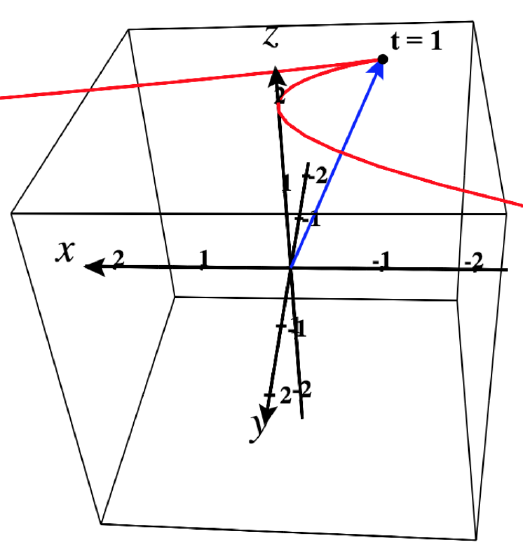
Since t=1 makes both components of ⇀r′ equal 0, we have ⇀r′(1)=⇀0, so we know that ⇀r is not smooth at t=1.
Note however that ⇀r is smooth at t=0, because although one of the components of ⇀r′ is 0, the other one is not.
Therefore we can conclude that ⇀r is smooth on the open intervals:
(−∞,1)and(1,∞)
Note in the figure that there is a cusp in the curve when t=1.
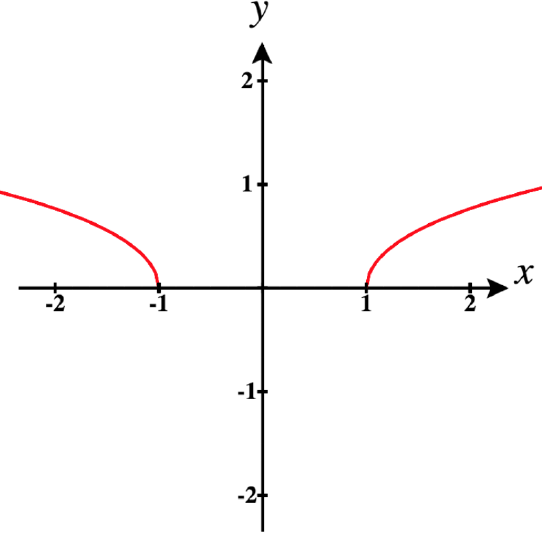
b. Next let ⇀r(t)=t3ˆi+√t2−1ˆj.
The domain of ⇀r is D⇀r:(−∞,−1]∪[1,∞), since t2−1 is less than 0 between −1 and 1.
Now we calculate ⇀r′(t). Since ⇀r(t)=t3ˆi+√t2−1ˆj, we have
⇀r′(t)=3t2ˆi+t√t2−1ˆj
Then, since we cannot have zero in the denominator, t=−1 and t=1 are not in the domain of ⇀r′. Thus, D⇀r′:(−∞,−1)∪(1,∞).
Lastly we determine if there are any values of t in D⇀r where ⇀r′(t)=⇀0.
Setting each component of ⇀r′(t) equal to 0 and solving for t we get:
3t2=0andt√t2−1=0t=0t=0
If t=0 were in the domain of ⇀r′, then ⇀r would not be smooth there, but since it is not in the domain, we have nothing to remove, and we can conclude that ⇀r is smooth on the entire domain of its derivative ⇀r′, that is,
⇀ris smooth on the open intervals:(−∞,−1)and(1,∞).
Observe the two separate smooth pieces of this function in the graph below.
c. Now let's consider, ⇀r(t)=t4ˆi+ln(t2+1)ˆj.
The domain of ⇀r is D⇀r:(−∞,∞), since the argument of the natural log function, t2+1, is always greater than 0 (In fact, it's always at least 1).
Now we calculate ⇀r′(t). Here
⇀r′(t)=4t3ˆi+2tt2+1ˆj
Then, since t2+1 cannot be 0, the domain of ⇀r′ is also all real numbers, D⇀r′:(−∞,∞).
Lastly we determine if there are any values of t in D⇀r where ⇀r′(t)=⇀0.
Setting each component of ⇀r′(t) equal to 0 and solving for t we get:
4t3=0and2tt2+1=0t=0t=0
Note that in this example, we have ⇀r′(0)=⇀0, so ⇀r is not smooth when t=0.
Therefore we conclude that ⇀r is smooth on the open intervals: (−∞,0)and(0,∞)
In this example, note that the motion reverses itself when t=0. We can't see this very well just by looking at its graph (see Figure 6). But if you evaluate ⇀r(t) for various values of t from −2 to 2, you'll see that the motion comes in towards the origin when t is negative, arrives at the origin when t=0, and then moves away from the origin as t becomes more positive.
d. Finally, let's look at a really interesting example: ⇀r(t)=(6cost−cos(6t))ˆi+(6sint−sin(6t))ˆj.
Its graph is the epicycloid shown above in Figure 3.
Again, ⇀r has no issues with its domain. We have D⇀r:(−∞,∞).
Calculating ⇀r′(t), we get:
⇀r′(t)=(−6sint+6sin(6t))ˆi+(6cost−6cos(6t))ˆj
There are still no issues, so D⇀r′:(−∞,∞).
Now for the most interesting part! For what values of t is ⇀r′(t)=⇀0?
Setting the two components equal to 0, we get:
−6sint+6sin(6t)=0and6cost−6cos(6t)=0
This time it's not as easy to quickly solve each of these equations for all values of t that make these component functions equal to 0. But if you read carefully, you'll see that it's really not that difficult to work out.
Rewriting the first equation gives us
sin(6t)=sint
To solve this equation, note that the periodic nature of the sine function means that its value is the same every 2π radians.
That is, for any integer n, we know
sin(t+2nπ)=sint
This means that one way for Equation ??? to be true would be for us to have
t+2nπ=6t
Solving this equation for t, we have:
t=2nπ5 for any integer n
On the interval 0≤t≤2π, this would give us the following solutions of Equation ???:
t=0,2π5,4π5,6π5,8π5,10π5=2π
Verifying that t=2π5 is a solution, we have:
sin(6⋅2π5)=sin(2π+2π5)=sin(2π5).✓
Note that the sine value (as the y-coordinate of a point on the unit circle) is the same for reflected angles about the \(y)-axis (e.g., in the first and second quadrants). That is,
sin(π−t)=sint
Incorporating the periodic nature of the sine function again, we obtain
sin((2n+1)π−t)=sint
Applying this identity to Equation ???, yields
sin((2n+1)π−t)=sin(6t)
So, another way for Equation ??? to be true would be for us to have
(2n+1)π−t=6t
Solving this equation for t, we have:
t=(2n+1)π7 for any integer n
On the interval 0≤t≤2π, this would give us the following solutions of Equation ???:
t=π7,3π7,5π7,7π7=π,9π7,11π7,13π7
Verifying that t=π7 is a solution, we have:
sin(6⋅π7)=sin(π−π7)=sin(π7).✓
Next we need to solve the equation from the setting the other component of ⇀r′(t) to 0. That is
6cost−6cos(6t)=0
Remember that not all values of t that make one of these components equal to 0 will cause ⇀r not to be smooth, but only those values of t that make both components equal to 0 at the same time. Once we solve this equation, we'll need to look for any values of t that are solutions to both of these equations.
Rewriting the equation above gives us
cos(6t)=cost
We can solve this equation using a similar process to what was shown for Equation ??? above.
As the cosine function is periodic in the same way that sine is, we have
cos(t+2nπ)=cost
which tells us Equation ??? will be true when
t+2nπ=6t
Solving this equation for t, we have:
t=2nπ5 for any integer n
Note that these values for t also made the first component of ⇀r′(t) equal to 0! Try verifying that one of these solutions satisfies Equation ???, as we showed for Equation ??? above.
Since the cosine values (as the x-coordinates of points on the unit circle) are the same for reflected angles about the x-axis (e.g. in the first and fourth quadrants). This is represented in the identity:
cos(−t)=cos(t)
Incorporating the periodic nature of the cosine function (as we did before), we obtain
cos(2nπ−t)=cos(t)
Applying this identity to Equation ???, yields
cos(2nπ−t)=cos(6t)
This is true when
2nπ−t=6t
Solving this equation for t, we have:
t=2nπ7 for any integer n
Although these may at first look like the same values as we found solved Equation ??? above, they are not.
On the interval 0≤t≤2π, this would give us the following solutions of Equation ???:
t=0,2π7,4π7,6π7,8π7,10π7,12π7,14π7=2π
Except for t=0 and t=2π that are already contained in the first set of solutions t=2nπ5 above, this second set of solutions does not add any additional values of t that would make both components of ⇀r′(t) equal to 0 at the same time.
We have now determined that ⇀r′(t)=⇀0 and therefore ⇀r is not smooth when t=2nπ5 for any integer n.
Removing these values from the interval 0≤t≤2π, we can say that ⇀r is smooth on the open intervals:
(0,2π5),(2π5,4π5),(4π5,6π5),(6π5,8π5), and (8π5,2π).
More generally, we can state that r is smooth on the open intervals:
(2nπ5,(2n+2)π5)for any integer n
Note in Figure 7, how there are cusps on the plot of this vector-valued function for each value of t at which ⇀r is not smooth.

Exercises:
For questions 32 - 40,
a. Determine any values of t at which ⇀r is not smooth.
b. Determine the open intervals on which ⇀r is smooth.
c. Graph the vector-valued function and describe its behavior at the points where it is not smooth.
32) ⇀r(t)=⟨3t,5t2−1⟩
33) ⇀r(t)=t3ˆi+5t2ˆj
- Answer
- a. ⇀r is not smooth at t=0, since ⇀r′(0)=⇀0.
b. ⇀r is smooth on the open intervals (−∞,0) and (0,∞).
c. There is a cusp when t=0.
34) ⇀r(t)=⟨5,2sin(t),cos(t)⟩
35) ⇀r(t)=⟨t3−3t2,7⟩
- Answer
- a. ⇀r is not smooth at t=0 and t=2, since ⇀r′(0)=⇀0 and ⇀r′(2)=⇀0.
b. ⇀r is smooth on the open intervals (−∞,0), (0,2), and (2,∞).
c. The motion on the curve reverses along the same path at both t=0 and t=2.
36) ⇀r(t)=t2ˆi+t3ˆj−5e−4tˆk
37) ⇀r(t)=⟨ln(t2+4t+5),t33−4t,5⟩
- Answer
- a. ⇀r is not smooth at t=−2, since ⇀r′(−2)=⇀0.
Since the domain of ⇀r is (−∞,∞), this is all we have to remove.
b. ⇀r is smooth on the open intervals (−∞,−2) and (−2,∞).
c. There is a cusp when t=−2.
38) ⇀r(t)=(5cost−cos5t)ˆi+(5sint−sin5t)ˆj, for 0≤t≤2π
39) ⇀r(t)=√t3+9t2ˆi+(t2+12t)ˆj+7ˆk
- Answer
- a. The domain of ⇀r is [−9,∞).
And ⇀r is not smooth at t=−6, since ⇀r′(−6)=⇀0.
The domain of ⇀r′ is (−9,∞), since ⇀r′ is undefined at t=−9.
b. ⇀r is smooth on the open intervals (−9,−6) and (−6,∞).
c. There is a cusp when t=−6.
40) ⇀r(t)=cos3tˆi+sintˆj, for 0≤t≤2π
- Answer
- a. The domain of ⇀r is (−∞,∞).
⇀r′(t)=−3(cos2t)(sint)ˆi+costˆj. It's domain is also (−∞,∞).
But note that both components have a factor of cost, so both components will be 0 when cost=0.
Therefore, ⇀r is not smooth at t=π2 and at t=3π2, since ⇀r′(π2)=⇀0 and ⇀r′(3π2)=⇀0. Note then that ⇀r is not smooth for any odd multiple of π2, that is for t=(2n+1)π2, for any integer value n.
b. ⇀r is smooth on the open intervals ((2n−1)π2,(2n+1)π2), for any integer value n.
c. There is a cusp when t=(2n+1)π2, for any integer value n.


