1.6: Lines and Planes

Lines

Our goal is to come up with the equation of a line given a vector v parallel to the line and a point (a,b,c) on the line. The figure (shown in 2D for simplicity) shows that if P is a point on the line then

\[ \langle x,y \rangle = P + tv\]

for some number \(t\).

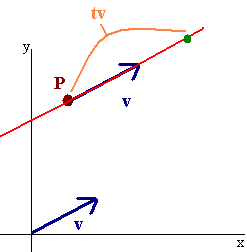
The picture is the same for 3D. The formula is given below.

Parametric Equations of a Line

The parametric equations for the line through the point \((a,b,c)\) and parallel to the vector v are

\[\langle x,y,z\rangle = \langle a,b,c\rangle + t\textbf{v}.\]

Example \(\PageIndex{1}\)

Find the parametric equations of the line that passes through the point \((1, 2, 3)\) and is parallel to the vector \(\langle 4, -2, 1\rangle\).

Solution

We write:

\[\langle x, y, z\rangle = \langle 1, 2, 3\rangle + t \langle 4, -2, 1\rangle = \langle 1 + 4t, 2 - 2t, 3 + t\rangle \]

or

\[ x(t) = 1 + 4t,\]

\[y(t) = 2 - 2t,\]

\[z(t) = 3 + t.\]

Exercise \(\PageIndex{1}\)

Find the parametric equations of the line through the two points \((2,1,7)\) and \((1,3,5)\).

Hint: a vector parallel to the line has tail at \((2,1,7)\) and head at \((1,3,5)\).

Planes

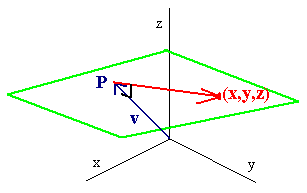
If S is a plane then a vector n is normal (perpendicular) to the plane if it is orthogonal to every vector that lies on the plane. Suppose that n is a normal vector to a plane and \((a,b,c)\) is a point on the plane. Let \((x,y,z)\) be a general point on the plane, then

\[ \langle x - a, y - b, z - c\rangle \]

is parallel to the plane, hence

\[\vec{n} \cdot \langle x - a, y - b, z - c\rangle = 0.\]

This defines the equation of the plane.

Example \(\PageIndex{2}\)

Find the equation of the plane that contains the point \((2,1,0)\) and has normal vector \(\langle 1,2,3\rangle \).

Solution

We have

\[\langle 1,2,3\rangle \cdot \langle x - 2,y - 1,z - 0\rangle = 0\]

so that

\[1(x - 2) + 2(y - 1) + 3z = 0\]

or

\[ x + 2y + 3z = 4.\]

Example \(\PageIndex{3}\)

Find the equation of the plane through the points

• \(P = (0,0,1)\)
• \(Q = (2,1,0)\)
• \(R = (1,1,1)\)

Solution

Let

\[\textbf{v} = Q-P = \langle 2,1,-1\rangle \]

and

\[\textbf{w} = R-P = \langle 1,1,0\rangle \]

then to find a vector normal to the plane, we find the cross product of \(v\) and \(w\):

\[v \times w = \begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{i}} & \hat{\textbf{i}} \\ 2 & 1 &-1 \\ 1 &1 0 \end{vmatrix} = \hat{\textbf{i}} - \hat{\textbf{j}} + \hat{\textbf{k}} \]

or

\[\langle 1, -1, 1\rangle .\]

We can now use the formula:

\[\langle 1, -1, 1\rangle \cdot \langle x, y, z - 1\rangle = 0\]

or

\[x - y + z - 1 = 0\]

or

\[x - y + z = 1\]

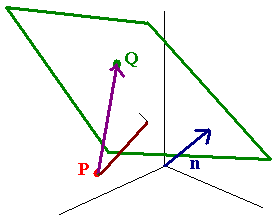
Distance Between a Point and a Plane

Let P be a point and Q be a point on a plane with normal vector n, then the distance between P and the plane is given by

Distance Between a Point \(P\) and a Plane With Normal Vector n

Let \(Q\) be a point on the plane with normal vector \(\vec{n}\). The the distance from the point \(P\) to this plane is given by

\[ Proj_nPQ = \dfrac{ ||PQ \cdot \vec{n}|| }{ || \vec{n}|| }.\]

Example \(\PageIndex{4}\)

Find the distance between the point \((1,2,3)\) and the plane

\[2x - y - 2z = 5.\]

Solution

The normal vector can be read off from the equation as

\[\vec{n} = \langle 2, -1, -2\rangle .\]

Now find a convenient point on the plane such as \(Q = (0, -5, 0)\). We have

\[Q = \langle -1, -7, -3\rangle \]

and

\[ \vec{n} \cdot PQ = -2 + 7 + 6 = 11.\]

We find the magnitude of n by taking the square root of the sum of the squares. The sum is

\[4 + 1 + 4 = 9\]

so

\[|| \vec{n} || = 3.\]

Hence the distance from the point to the plane is \(\frac{11}{3}\).

The Angle Between Two Planes

The angle between two planes is given by the angle between the normal vectors.

Example \(\PageIndex{5}\)

Find the angle between the two planes

\[ 3x - 2y + 5z = 1\]

and

\[4x + 2y - z = 4.\]

We have the two normal vectors are

\[ \vec{n} = \langle 3,-2,5\rangle \]

and

\[\vec{m} = \langle 4,2,-1\rangle .\]

We have

\[\vec{n} \cdot \vec{ m} = 3\]

\[ || \vec{n} || = \sqrt{38}\]

\[ || \vec{m} || = \sqrt{21}\]

hence the angle is

\[ \cos^{-1} \left(\dfrac{3}{\sqrt{38}\sqrt{21}} \right) = 1.46 \, rad.\]

Larry Green (Lake Tahoe Community College)

• Integrated by Justin Marshall.