1.7: Tangent Planes and Normal Lines

Tangent Planes

Let \(z = f(x,y)\) be a function of two variables. We can define a new function \(F(x,y,z)\) of three variables by subtracting \(z\). This has the condition

\[ F(x,y,z) = 0.\]

Now consider any curve defined parametrically by

\[x = x(t), \;\;\; y = y(t), \;\;\; z = z(t).\]

We can write,

\[F(x(t), y(t), z(t)) = 0.\]

Differentiating both sides with respect to \(t\), and using the chain rule gives

\[F_x(x, y, z) x' + F_y(x, y, z) y' + F_z(x, y, z) z' = 0\]

Notice that this is the dot product of the gradient function and the vector \(\langle x',y',z'\rangle \),

\[\nabla F \cdot \langle x', y', z'\rangle = 0.\]

In particular the gradient vector is orthogonal to the tangent line of any curve on the surface. This leads to:

Definition: Tangent Plane

Let \(F(x,y,z)\) define a surface that is differentiable at a point \((x_0,y_0,z_0)\), then the tangent plane to \(F ( x, y, z )\) at \(( x_0, y_0, z_0)\) is the plane with normal vector

\[ \nabla \, F(x_0,y_0,z_0) \]

that passes through the point \((x_0,y_0,z_0)\) . In particular, the equation of the tangent plane is

\[ \nabla \, F(x_0,y_0,z_0) \cdot \langle x - x_0 , y - y_0 , z - z_0 \rangle = 0. \]

Example \(\PageIndex{1}\)

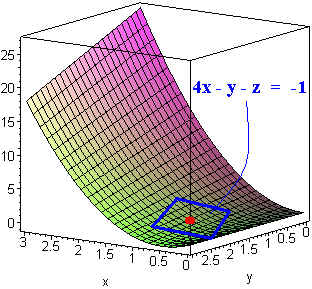
Find the equation of the tangent plane to

\[ z = 3x^2 - xy \]

at the point \((1,2,1)\).

Solution

We let

\[F(x,y,z) = 3x^2 - xy - z\]

then

\[\nabla F = \langle 6x - y, -x, -1\rangle . \]

At the point \((1,2,1)\), the normal vector is

\[\nabla F(1,2,1) = \langle 4, -1, -1\rangle . \]

Now use the point normal formula for a plan

\[\langle 4, -1, -1\rangle \cdot \langle x - 1, y - 2, z - 1\rangle = 0\]

or

\[4(x - 1) - (y - 2) - (z - 1) = 0.\]

Finally we get

\[ 4x - y - z = 1.\]

Normal Lines

Given a vector and a point, there is a unique line parallel to that vector that passes through the point. In the context of surfaces, we have the gradient vector of the surface at a given point. This leads to the following definition.

Definition: Normal Line

Let \(F(x,y,z)\) define a surface that is differentiable at a point \((x_0,y_0,z_0)\), then the normal line to \(F(x,y,z)\) at \((x_0,y_0,z_0)\) is the line with normal vector

\[ \nabla \, F(x_0,y_0,z_0) .\]

that passes through the point \((x_0,y_0,z_0)\) . In Particular the equation of the normal line is

\[ x(t) = x_0 + F_x(x_0,y_0,z_0) t, \]

\[ y(t) = y_0 + F_y(x_0,y_0,z_0) t, \]

\[ z(t) = z_0 + F_z(x_0,y_0,z_0) t. \]

Example \(\PageIndex{2}\)

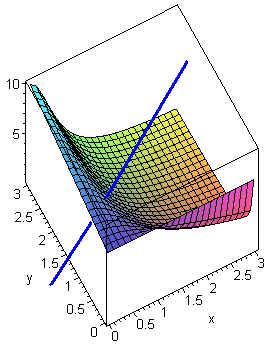
Find the parametric equations for the normal line to

\[ x^2yz - y + z - 7 = 0 \]

at the point \((1,2,3)\).

Solution

We compute the gradient:

\[\nabla F = \langle 2xyz, x^2z - 1, x^2y + 1\rangle = \langle 12, 2, 3\rangle .\]

Now use the formula to find

\[x(t) = 1 + 12t, \;\;\; y(t) = 2 + 2t, \;\;\; z(t) = 3 + 3t.\]

The diagram below displays the surface and the normal line.

Angle of Inclination

Given a plane with normal vector n the angle of inclination, \(q\) is defined by

\[\cos q = \dfrac{|\textbf{n} \cdot k|}{ ||\textbf{n} ||}. \]

More generally, if \( F(x,y,z) = 0 \) is a surface, then the angle of inclination at the point \((x_0,y_0,z_0)\) is defined by the angle of inclination of the tangent plane at the point with

\[ \cos\,q = \dfrac{ | \nabla F(x_0, y_0, z_0) \cdot \textbf{k}| }{|| \nabla F(x_0, y_0, z_0)||}. \]

Example \(\PageIndex{3}\)

Find the angle of inclination of

\[ \dfrac{x^2}{4} + \dfrac{y^2}{4} + \dfrac{z^2}{8} = 1\]

at the point \((1,1,2)\).

Solution

First compute

\[ \nabla F = \langle \dfrac{x}{2}, \dfrac{y}{2}, \dfrac{z}{4}\rangle .\]

Now plug in to get

\[\nabla F(1,1,2) = \langle \dfrac{1}{2}, \dfrac{1}{2}, \dfrac{1}{2} \rangle .\]

We have

\[|\langle \dfrac{1}{2} , \dfrac{1}{2} , \dfrac{1}{2} \rangle \cdot \hat{\textbf{k}} | = \dfrac{1}{2} .\]

Also,

\[||\langle \dfrac{1}{2} , \dfrac{1}{2} , \dfrac{1}{2} \rangle || = \dfrac{\sqrt{3}}{2} .\]

Hence

\[ \cos q = \dfrac{\frac{1}{2}}{( \frac{\sqrt{3}}{2} )} = \dfrac{1}{\sqrt{3}} . \]

So the angle of inclination is

\[q = \cos^{-1}(\dfrac{1}{\sqrt{3}}) = 0.955 \text{ radians} .\]

The Tangent Line to a Curve

Example \(\PageIndex{4}\)

Find the tangent line to the curve of intersection of the sphere

\[x^2 + y^2 + z^2 = 30\]

and the paraboloid

\[z = x^2 + y^2\]

at the point \((1,2,5)\).

Solution

We find the gradient of the two surfaces at the point

\[ \nabla(x^2 + y^2 + z^2) = \langle 2x, 2y, 2z\rangle = \langle 2, 4,10\rangle \]

and

\[\nabla (x^2 + y^2 - z) = \langle 2x, 2y, -1\rangle = \langle 2, 4, -1\rangle .\]

These two vectors will both be perpendicular to the tangent line to the curve at the point, hence their cross product will be parallel to this tangent line. We compute

\[ \begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{j}} & \hat{\textbf{k}} \\ 2 & 4 & 10 \\ 2 & 4 & -1 \end{vmatrix} = -44 \hat{\textbf{i}} + 22 \hat{\textbf{j}}. \]

Hence the equation of the tangent line is

\[x(t) = 1 - 44t y(t) = 2 + 22t z(t) = 5.\]

Larry Green (Lake Tahoe Community College)

• Integrated by Justin Marshall.