1.1: Divisors and Congruences

Last updated
Save as PDF

Page ID: 60294

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Definition 1.1

Given two numbers $a$ and $b$. A multiple $b$ of $a$ is a number that satisfies $b = ac$. A divisor $a$ of $b$ is an integer that satisfies $ac = b$ where $c$ is an integer. We write $a|b$. This reads as $a$ divides $b$ or a is $a$ divisor of $b$.

Definition 1.2

Let $a$ and $b$ non-zero. The greatest common divisor of two integers $a$ and $b$ is the maximum of the numbers that are divisors of both $a$ and $b$. It is denoted by $\gcd(a, b)$. The least common multiple of $a$ and $b$ is the least of the positive numbers that are multiples of both $a$ and $b$. It is denoted by $\mbox{lcm}(a ,b)$.

Note that for any $a$ and $b$ in $\mathbb{Z}$, $\gcd(a, b) \ge 1$, as 1 is a divisor of every integer. Similarly $\mbox{lcm} (a, b) \le |ab|$.

Definition 1.3

A number $a > 1$ is prime in $\mathbb{N}$ if its only divisors in $\mathbb{N}$ are $a$ and 1 (the so-called trivial divisors). A number $a > 1$ is composite if it has more than 2 divisors. (The number 1 is neither.)

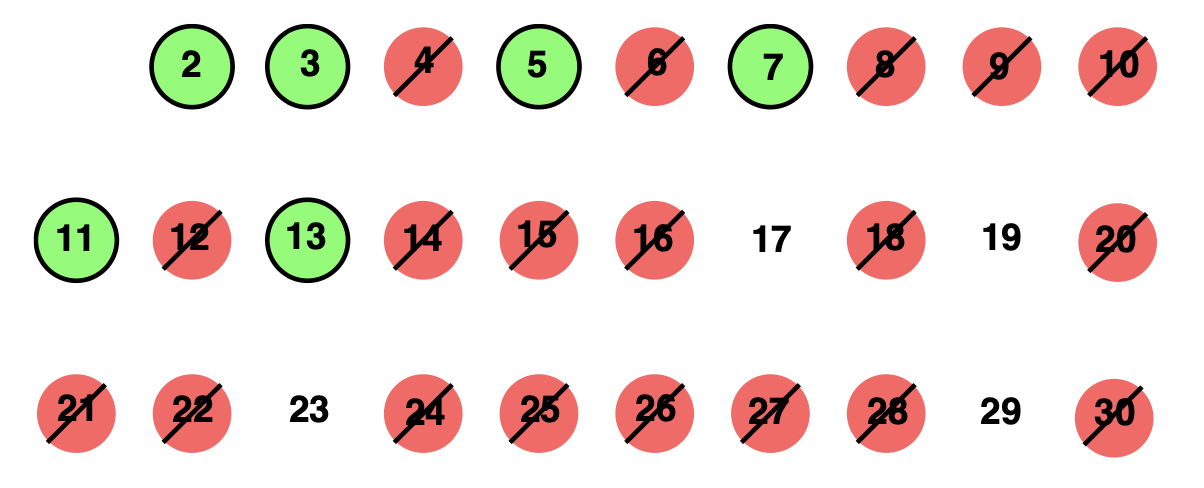
$Screen Shot 2021-04-02 at 3.42.15 PM.png$

Figure 1. Eratosthenes’ sieve up to $n = 30$. All multiples of a less than $\sqrt{31}$ are cancelled. The remainder are the primes less than $n = 31$.

An equivalent definition of prime is a natural number with precisely two (distinct) divisors. Eratosthenes’ sieve is a simple and ancient method to generate a list of primes for all numbers less than, say, 225. First, list all integers from 2 to 225. Start by circling the number 2 and crossing out all its remaining multiples: 4, 6, 8, etcetera. At each step, circle the smallest unmarked number and cross out all its remaining multiples in the list. It turns out that we need to sieve out only multiples of $\sqrt{225} = 15$ and less (see exercise 2.4). This method is illustrated if Figure 1. When done, the primes are those numbers that are circled or unmarked in the list.

Definition 1.4

Let $a$ and $b$ in $\mathbb{Z}$. Then $a$ and $b$ are relatively prime if $\gcd(a, b) = 1$.

Definition 1.5

Let $a$ and $b$ in $\mathbb{Z}$ and $m \in \mathbb{N}$. Then $a$ is congruent to $b$ modulo m if $a+my = b$ for some $y \in \mathbb{Z}$ or $m | (b-a)$. We write

\[\begin{array}{ccccc} {a = _{m}b}&{\mbox{or}}&{a = b \mod m}&{\mbox{or}}&{a \in b+m \mathbb{Z}} \end{array} \nonumber\]

Definition 1.6

The residue of $a$ modulo $m$ is the (unique) integer $r$ in $\{0, \cdots, m-1\}$ such that $a = _{m}r$. It is denoted by $\mbox{Res} _{m}(a)$.

These notions are cornerstones of much of number theory as we will see. But they are also very common in all kinds of applications. For in- stance, our expressions for the time on the clock are nothing but counting modulo 12 or 24. To figure out how many hours elapse between 4pm and 3am next morning is a simple exercise in working with modular arithmetic, that is: computations involving congruences.